Методы решения матричных игр

Преобразование матричных игр.

Стратегия А_i называется доминирующей над стратегией A_k, если в строке A_i стоят выигрыши не меньшие, чем в соответствующих клетках A_k и из них по крайней мере один действительно больше, чем в соответствующей клетке строки A_k. Если же все выигрыши строки A_i равны соответствующим выигрышам строки A_k, то стратегия называется дублирующей. Аналогично для стратегий игрока В: доминирующей называется та его стратегия, при которой везде стоят выигрыши не большие, чем в соответствующих клетках другой, и по крайне мере один из них действительно меньше; дублирование означает полное повторение одного столбца другим. Все дублирующие стратегии и те, для которых есть доминирующие, можно отбросить.

ПРИМЕР 5.2.

	В1	В2	В3	В4	В5
A1	4	7	2	3	4
A2	3	5	6	8	9
А3	4	4	2	2	8
A4	3	6	1	2	4
A5	3	5	6	8	9

A₅ дублирует A₂, A₁ доминирует над A₄. Отбросив A₅ и A₄, получим

	В1	В2	В3	В4	В5
A1	4	7	2	3	4
A2	3	5	6	8	9
А3	4	4	2	2	8

В₃ доминирует над В₄ и В₅ (В стремится отдать поменьше), а В₁ над В₂

	В1	В3
A1	4	2
A2	3	6
А3	4	2

Удалим дублирующую строку А₃

	В1	В3
A1	4	2
A2	3	6

Упрощая матрицу игры, можно прийти к играм 2Ä2, 2Än, mÄ2, которые допускают геометрическую интерпретацию, что упрощает поиск оптимальной стратегии.

Сведение к задаче линейного программирования. Пусть имеется игра mÄn без седловой точки c выигрышами a_ij >0 (это всегда можно сделать, прибавляя ко всем членам матрицы достаточно большое число, от чего цена игры увеличится, но решение не изменится). Пусть цена игры – v (v>0, т.к. матрица игры положительна)

Требуется найти решение игры, т.е. две оптимальные смешанные стратегии.

S_A=(p₁, p₂, …, p_m), S_B=(q₁, q₂, …q_n), дающие каждой стороне максимально возможный для неё выигрыш (минимальный проигрыш)

Предположим, что мы применяем свою оптимальную стратегию, а игрок В отступает от своей оптимальной смешанной стратегии и пользуется чистыми стратегиями В₁, В_2, … В_n. Тогда наш выигрыш не может быть меньше, чем v. Можно составить систему неравенств:

a₁₁ p_{1 +} a₂₁ p_{2 +} …+ a_m1 p_m ³ v

…

a_1n p_{1 +} a_2n p_{2 +} …+ a_{m n} p_m ³ v

Разделим неравенства на v и обозначим x₁ =p₁ / v, … x_m =p_m / v

Тогда условия примут вид

a₁₁ х_{1 +} a₂₁ х_{2 +} …+ a_m1 х_m ³ 1

…

a_1n х_{1 +} a_2n х_{2 +} …+ a_{m n} х_m ³ 1

где х_i – неотрицательные переменные.

Т.к. p₁ +p₂ +…,+p_m=1, то х₁ +х₂ +…+х_m=1/v

v – наш гарантированный выигрыш и мы хотим сделать его максимальным. Получили задачу линейного программирования: найти х_i³0, удовлетворяющие системе неравенств и обращающие в минимум линейную функцию L = х₁ + х₂ + …+ х_m. Следовательно, все методы линейного программирования можно использовать для нахождения оптимального решения игры. И наоборот, методы решения игры, можно применить для решения задач линейного программирования.

Метод итераций – один из самых простых численных методов решения игр (приближённый метод). Идея метода: разыгрывается «мысленный эксперимент», в котором А и В поочерёдно применяют друг против друга свои стратегии, стремясь выиграть побольше (проиграть поменьше). Эксперимент состоит из ряда «партий» игры. Игрок А выбирает произвольно одну из своих стратегий A_i. Противник отвечает ему той из своих стратегий B_j, которая хуже всего для А при стратегии A_i. Далее А выбирает ту стратегию A_k, которая даёт ему максимальный выигрыш при стратегии B_j. Теперь противник отвечает той стратегией, которая является наихудшей для нашей смешанной стратегии (A_i, A_k), в которой до сих пор применённые стратегии встречаются с равными вероятностями=1/2. И так далее: на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той стратегией, которая является оптимальной для него относительно смешанной стратегии другого, в которую все применённые ранее стратегии входят пропорционально частотам их применения. Такой метод сходится: при увеличении числа партий средний выигрыш на 1 партию будет стремиться к цене игры, а частоты применения стратегий – к вероятностям в оптимальных смешанных стратегиях.

ПРИМЕР 5.3.

Рассмотрим задачу «про пальцы». Увеличим на 5 все элементы матрицы. Цена игры также увеличится на 5.

	В1	В2	В3
A1	7	2	9
A2	2	9	0
А3	9	0	11

Проведем мысленный эксперимент:

k	i	В1	В2	В3	J	A1	A2	А3	v		v^*
		9 11 13 15 22 31	0 9 18 27 29 29	11 11 11 11 20 31					4.5 3.67 2.75 4.0 4.84	5.5 6.6 5.5	4.5 6.75 4.84 4.13 5.3 5.17 4.79 5.3 4.78 5.1 4.87 5.2 4.84 5.07 4.9

v – нижняя оценка игры, равная минимальному накопленному выигрышу, делённому на число партий. Аналогично 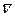– верхняя оценка. v^* – среднееарифметическое между оценками.

v^*»5, p₁^*=4/15»0.266, p₂^*=7/15»0.468, p₃^*=4/15»0.266

q₁^*=2/15»0.133, q₂^*=8/15»0.534, q₃^*=5/15»0.333

v»0, p₁= q₁ =1/4=0.25, p₂= q₂ =1/2=0.5, p₃= q₃ =1/4=0.25

Дата добавления: 2014-01-20