Определение предельного коэффициента раздачи при разрыве кромки

Считаем, что кромка заготовки деформируется в условиях линейных схем НДС. Тогда за критическую величину деформаций принимаем как и при линейной схеме деформаций , то есть

,

,

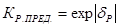
Последнее выражение дает оценочное значение предельного коэффициента раздачи.

Иногда для относительно толстых заготовок, для которых

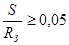
предельный коэффициент определяют с учетом давления заготовки на оправку. Тогда условием формообразования можно считать условие, при котором давление достигает максимума. Для этого используют уравнения равновесия элемента кромки заготовки на ось, перпендикулярную рабочей поверхности заготовки.

Схема действия сил

Получим уравнение Лапласа

,

,

,

.

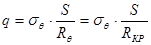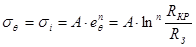Величина S по мере раздачи уменьшает свое значение.

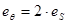- для линейной схемы.

,

.

(*),

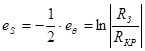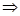
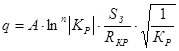Анализируя данное выражение видно, что коэффициент раздачи оказывает взаимно противоположное влияние разных сомножителей. , который учитывает упрочнение, увеличивает выражение, а который учитывает толщину – уменьшает.

Имеет место такой коэффициент раздачи, при котором достигает экстремума.

.

Таким образом, предварительно преобразовав уравнение (*) разделив и умножив на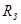получим

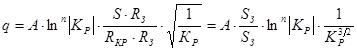. const

Из данного выражения находим . Найденный коэффициент, как правило, имеет большее значение, нежели в первом случае.

Смысл этого критерия: как только образец начинает сильно утоняться, давление падает, в этот момент и фиксируется

Практика отличается от теории, так как есть влияние третьего напряжения, влияние анизоторопии по длине.

При раздаче большое значение имеет состояние кромки заготовки. Наибольшее значение имеет место при полированной кромке, близкое к состоянию поверхности прокатанного листа.

Выбор предельного коэффициента в случае гофрообразования и разрыва кромки определен наименьшим значением

В случае, если общий коэффициент раздачи больше предельного необходимо вести процесс в несколько переходов.

Для толстостенных заготовок, когда 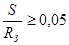, предельный коэффициент которых определен разрывом кромки, необходимо как правило производить промежуточные отжиги, используя одну и ту же штамповую оснастку. В этом случае все коэффициенты раздачи считаем одинаковыми

,

.

Для тонкостенных заготовок, теряющих устойчивость, возможно 2 варианта.

1. Для тонкостенных высокопластичных заготовок возможно провести многократную раздачу без промежуточного отжига, но в разной штамповой оснастке.

1 – пуансон,

2 – заготовка,

3 – оправка.

2. Для тонкостенных и малопластичных заготовок кроме разной штамповой оснастки необходимо применять промежуточный отжиг. Такие материалы являются наиболее трудоемкими в обработке.

Дата добавления: 2014-01-20