Переход от одного опорного решения к другому

Грузы надо перераспределить, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.

Для свободной клетки с строится цикл, все вершины которого кроме одной находятся в занятых клетках; углы прямые, число вершин чётное. Около свободной клетки цикла ставится знак (+), затем поочерёдно проставляются знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т. д. до тех пор, пока не получим оптимальное решение.

Рассмотрим переход от одного опорного решения к другому на заданном примере.

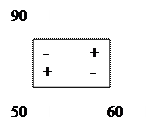
Строим цикл для клетки (1, 3), имеющей положительную оценку, и перераспределяем груз, тем самым получив новый цикл:

		→

Bj Ai				ui
		2		2
		4
	vj		-2

, следовательно, решение не оптимальное.

Получим новое решение перераспределением грузов.

Bj Ai				ui
	vj		-2

Все оценки свободных клеток отрицательные, следовательно решение оптимальное.

Стоимость транспортных расходов равна 1280 усл. ед. По сравнению с исходным опорным решением транспортные расходы уменьшились на 1610-1280=330 усл. ед.

Альтернативный оптимум в транспортных задачах

Признаком наличия альтернативного оптимума в транспортной задаче является равенство нулю хотя бы одной из оценок свободных переменных в оптимальном решении (). Сделав перераспределение грузов относительно клетки, имеющей 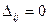, получим новое оптимальное решение (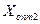), при этом значение целевой функции не изменится. Если одна оценка свободных переменных равна нулю, то оптимальное решение находится в виде

,

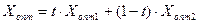где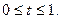

Пример. На трёх складах имеется мука в количестве 60, 130 и 90 т, которая должна быть в течение месяца доставлена четырём хлебозаводам в количестве: 30, 80, 60, 110 т соответственно.

Составить оптимальный план перевозок, имеющий минимальные транспортные расходы, если стоимость доставки 1 т муки на хлебозаводы задана матрицей

.

ОТВЕТ.

, , .

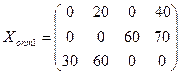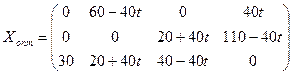Стоимость транспортных расходов составляет 1550 усл. ед.

Вырожденность в транспортных задачах

При решении транспортной задачи может оказаться, что число занятых клеток меньше, чем m + n – 1. В этом случае задача имеет вырожденное решение. Для возможного его исключения нужно ввести в свободную клетку с наименьшей оценкой нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и каждом столбце было не менее одной занятой клетки.

Пример. Фирма осуществляет поставку бутылок на 4 завода, занимающиеся производством прохладительных напитков. Она имеет три склада, причём на складе 1 находится 6000 бутылок, на складе 2 – 3000 бутылок и на складе 3 – 4000 бутылок. Первому заводу требуется 4000 бутылок, второму заводу – 5000 бутылок, третьему заводу – 1000 бутылок и 4 – 3000. Матрицей

задана стоимость перевозки одной бутылки от каждого склада к каждому заводу.

Как следует организовать доставку бутылок на заводы, чтобы стоимость перевозки было минимальной?

РЕШЕНИЕ. Запишем исходные данные в распределительную таблицу, найдём исходное опорное решение по методу минимального тарифа. Число заполненных клеток равно 5, m+n– 1=6, следовательно, задача является вырожденной.

Для исключения вырожденности необходимо в какую-то клетку ввести нулевую поставку. Такая клетка становится условно занятой, она нужна для вычисления потенциалов занятых клеток. Эта клетка должна иметь наименьший тариф по сравнению с другими клетками, которые могут быть условно занятыми.

Поместим нулевую поставку в клетку (3, 2), после чего появится возможность вычислить все потенциалы.

Bj Ai					ui
1 6000
2 3000					-1
3 4000					-1
vj

Все оценки свободных клеток отрицательные, следовательно, получили оптимальное решение:

.

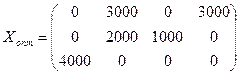Стоимость транспортных расходов при данном оптимальном решении составит 52000 усл. ед.

Открытая транспортная задача

При открытой транспортной задаче сума запасов не совпадает с суммой потребностей, т. е.

.

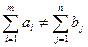При этом:

а) если , то объём запасов превышает объём потребления, все потребители будут удовлетворены полностью и часть запасов останется невывезенной. Для решения задачи вводят фиктивного (п + 1)-го потребителя, потребности которого .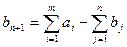

Модель такой задачи будет иметь вид

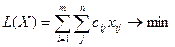
при ограничениях:

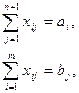
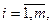
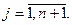
б) если 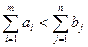, то объём потребления превышает объём запасов, часть потребностей останется неудовлетворённой. Для решения задачи вводят фиктивного (т + 1)-го поставщика, потребности которого .

Модель такой задачи будет иметь вид

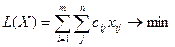
при ограничениях:

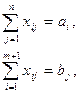
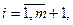
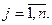
При введении фиктивного поставщика или потребителя открытая транспортная задача становится закрытой и решается по ранее рассмотренному алгоритму для закрытых транспортных задач, причём тарифы, соответствующие фиктивному поставщику или потребителю, больше или равны наибольшему из всех транспортных тарифов, иногда их считают равными нулю. В целевой функции фиктивный поставщик или потребитель не учитываются.

Определение оптимального варианта перевозки грузов

Задача. Составить оптимальный план перевозки грузов от трёх поставщиков с грузами 240, 40, 110 т к четырём потребителям с запросами 90, 190, 40 и 130 т. Стоимость перевозок единицы груза от каждого поставщика к каждому потребителю даны матрицей

.

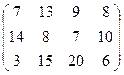РЕШЕНИЕ. Запасы грузов у поставщиков: 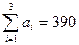т. Запросы потребителей: т; так как 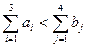, то вводим фиктивного поставщика с грузом а_4ф = 450 – 390 = 60 т.

Тариф фиктивного поставщика 4ф примем равным 20 усл. ед.

Bj Ai					ui
1 240	7	13
2 40	14		7		-5
3 110	3	15			-2
4ф 60
vj

Так как т + п – 1 = 7, а число занятых клеток равно 6, то для исключения вырожденности введём в клетку (2, 2) нулевую поставку. Оценки свободных клеток: , .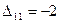

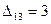Оценка свободной клетки (1, 3) больше нуля, перераспределим грузы:

Запишем полученное перераспределение грузов в табл.:

Bj Ai					ui
1 240
2 40			7		-5
3 110					-2
4ф 60
vj

Имеем

, , , , , , , , .

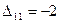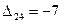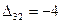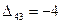Получили оптимальное решение:

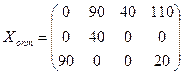
Стоимость транспортных расходов – 3120 усл. ед.

Приложение транспортных моделей к решению некоторых экономических задач.

Алгоритм и методы решения транспортных задач могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов c_ij имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие:

- оптимальное закрепление за станками операций по обработке деталей. В них c_ij является таким экономическим показателем, как производительность. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения c_ij берутся с отрицательным знаком;

- оптимальные назначения, или проблема выбора. Имеется т механизмов, которые могут выполнять т различных работ с производительностью c_ij. Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности;

- задача о сокращении производства с учётом суммарных расходов на изготовление и транспортировку продукции;

- увеличение производительности автомобильного транспорта за счёт минимизации порожнего пробега. Уменьшение порожнего пробега сократит количество автомобилей для перевозок, увеличив их производительность;

- решение задач с помощью метода запрещения перевозок. Используется в том случае, если груз от некоторого поставщика по каким-то причинам не может быть направлен одному из потребителей. Данное ограничение можно учесть, присвоив соответствующей клетке достаточно большое значение стоимости, тем самым в эту клетку не будут производиться перевозки.

Выбор оптимального варианта использования производственного оборудования

Задача. На предприятии имеется три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч.

Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.

Производительность каждой группы станков на каждую операцию задана матрицей

.

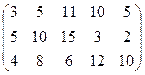РЕШЕНИЕ. Воспользуемся алгоритмом решения закрытой транспортной задачи.

Так как в задаче требуется найти максимум, а согласно алгоритму транспортной задачи находится минимум, тарифы умножим на (-1).

Bj Ai						ui
1 100	-3	-5	-11	-10	-5
2 250	-5	-10	-15	-3	-2	-2
3 180	-4	-8	-6	-12	-10	-5
vj	-3	-8	-13	-7	-5

Находим оценки свободных клеток: , , .

Так как > 0, перераспределим грузы, получим

Полученное перераспределение грузов занесём в табл.

Bj Ai						ui
1 100	-3	-5	-11	-10	-5
2 250	-5	-10	-15	-3	-2	-2
3 180	-4	-8	-6	-12	-10	-2
vj	-3	-8	-13	-10	-8

Оценки свободных клеток составляют

, , , , , , , .

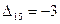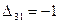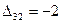Найденное решение является оптимальным, так как все оценки свободных клеток отрицательные. Итак,

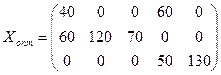
Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч соответственно, на второй группе – операции 1, 2 и 3 продолжительностью 60, 120 и 70 ч соответственно, на третьей группе – операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5170 шт.

Дата добавления: 2014-01-11