Основные аналитические показатели динамики

ПОКАЗАТЕЛИ	Базисные	Цепные
Абсолютный прирост (D)	Dб =	Dц =
Темп роста (Тр): в коэффициентах -     в процентах -	Трб = Трб =* 100	Трц = Трц = * 100
Темп прироста (Тп): в коэффициентах - в процентах -	Тпб = Трб – 1 Тпб = Трб - 100	Тпц = Трц – 1 Тпц = Трц - 100

Обозначения: y_i - i-уровень ряда динамики,

y₁ - первый (базисный) уровень;

Таким образом, абсолютный прирост есть разность уровней, а темп роста - отношение уровней.

Задача

Динамика продаж товара в регионе характеризуется следующими данными [1]:

Таблица 5.2

ГОДЫ (t)
Объём продаж, тыс. ед. (y)	2,9	3,1	4,2	3,8	4,8

Исследовать динамику продаж данного товара в регионе.

РЕШЕНИЕ

Исследование динамики проведем с помощью соответствующих аналитических показателей. На первом этапе рассчитаем базисные показатели (базисный год - 2000).

Абсолютный прирост (D_б):

2001 г. к 2000 г. 3,1 - 2,9 = 0,2 тыс.ед.

2002 г. к 2000 г. 4,2 - 2,9 = 1,3 тыс.ед.

2003 г. к 2000 г. 3,8 - 2,9 = 0,9 тыс.ед.

2004 г. к 2000 г. 4,8 - 2,9 = 1,9 тыс.ед.

Темп роста (Тр_б):

2001 г. к 2000 г. 3,1: 2,9 = 1,069 * 100 = 106,9 %

2002 г. к 2000 г. 4,2: 2,9 = 1,448 * 100 = 144,8 %

2003 г. к 2000 г. 3,8: 2,9 = 1,310 * 100 = 131,0 %

2001 г. к 2000 г. 4,8: 2,9 = 1,655 * 100 = 165,5 %

Темп прироста (Тп_б):

2001 г. к 2000 г. 106,9 - 100 = 6,9 %

2002 г. к 2000 г. 144,8 - 100 = 44,8 %

2003 г. к 2000 г. 131,0 - 100 = 31,0 %

2004 г. к 2000 г. 165,5 - 100 = 65,5 %

Цепные показатели рассчитываются следующим образом:

Абсолютный прирост (D_ц):

2001 г. к 2000 г. 3,1 - 2,9 = 0,2 тыс.ед.

2002 г. к 2001 г. 4,2 - 3,1 = 1,1 тыс.ед.

2003 г. к 2002 г. 3,8 - 4,2 = -0,4 тыс.ед.

2004 г. к 2003 г. 4,8 – 3,8 = 1,0 тыс.ед.

Темп роста (Тр_ц):

2001 г. к 2000 г. 3,1: 2,9 = 1,069 * 100 = 106,9 %

2002 г. к 2001 г. 4,2: 3,1 = 1,355 * 100 = 135,5 %

2003 г. к 2002 г. 3,8: 4,2 = 0,905 * 100 = 90,5 %

2004 г. к 2003 г. 4,8: 3,8 = 1,263 * 100 = 126,3 %

Темп прироста (Тп_ц):

2001 г. к 2000 г. 106,9 - 100 = 6,9 %

2002 г. к 2001 г. 135,5 - 100 = 35,5 %

2003 г. к 2002 г. 90,5 - 100 = -9,5 %

2004 г. к 2003 г. 126,3 – 100 = 26,3 %

Таблица 5.3

Результаты расчётов (аналитические показатели динамики)

Годы (t)	Число разводов, тыс. ед. (y)	Dб, тыс. ед.	Dц, тыс. ед.	Трб, %	Тпб, %	Трц, %	Тпц, %
	2,9	-	-	-	-	-	-
	3,1	0,2	0,2	106,9	6,9	106,9	6,9
	4,2	1,3	1,1	144,8	44,8	135,5	35,5
	3,8	0,9	-0,4	131,0	31,0	90,5	-9,5
	4,8	1,9	1,0	165,5	65,5	126,3	26,3

Анализ можно дополнить расчётом средних показателей динамики.

Средний абсолютный прирост - это средняя арифметическая из цепных абсолютных приростов:

Δ = 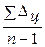= 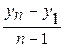, где: n - число уровней ряда; y_{n и} y_{1 -} соответственно последний и первый уровни ряда.

По данным таблицы 5.3: Δ =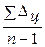= = = 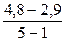0, 475.

Вывод: объём продаж в среднем ежегодно возрастал на 0,475 тыс. ед.

Внимание: отрицательное значение среднего абсолютного прироста свидетельствует о снижении уровня изучаемого показателя!

Средний темп роста – это средняя геометрическая из цепных коэффициентов (темпов) роста:

Тр = 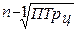=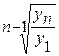, где ПТр_ц – произведение цепных коэффициентов роста.

По данным таблицы 5.3: Тр = 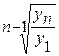= = 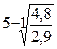1,134 = 113,4 %.

Исходя из этого, можно рассчитать средний темп прироста:

Тп = Тр - 100 = 13,4 %.

Внимание: отрицательное значение среднего темпа прироста так же говорит о снижении уровня изучаемого показателя!

Вывод: объём продаж в среднем ежегодно возрастал на 13,4 % (113,4 - 100).

Особое значение имеет расчёт среднего уровня ряда динамики (). Его расчёт зависит от вида и особенностей рядов динамики. Рассмотрим 3 случая.

1. ИНТЕРВАЛЬНЫЙ РЯД

Вернёмся к задаче про продажу товара в регионе (таблица 5.2). Найдём среднегодовой объём продаж:

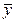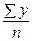= = = 3,76 тыс. ед.

Расчёт ведётся по формуле средней арифметической простой.

2. МОМЕНТНЫЙ РЯД С РАВНЫМИ ПРОМЕЖУТКАМИ МЕЖДУ ДАТАМИ

Задача

Данные о списочной численности персонала фирмы (чел):

Даты (t)	1 января	1 февраля	1 марта	1 апреля
Численность персонала, чел. (y)

Найти среднемесячную численность персонала фирмы за 1 квартал.

= = = 57 чел.

Расчёт ведётся по формуле средней хронологической.

3. МОМЕНТНЫЙ РЯД С НЕРАВНЫМИ ПРОМЕЖУТКАМИ МЕЖДУ ДАТАМИ

Задача

Данные о численности осуждённых в колониях региона:

Даты (t)	1.04	6.04	16.04	29.04
Численность осуждённых, тыс. чел. (y)	3,4	3,5	3,1	3,0

Примечание: указанные даты - это даты, когда менялась численность. В остальные дни она оставалась неизменной.

Исчислить среднюю численность осуждённых в апреле.

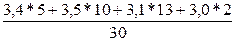= = = 3,28 тыс.чел.

Расчёт ведётся по формуле средней арифметической взвешенной.

В числителе каждый уровень умножается на число дней, в течение которого он не менялся. В знаменателе - число дней в апреле.

[1] Это - интервальный ряд динамики, так как время t представлено периодами - годами.

Дата добавления: 2014-01-20