Метод неопределенных множителей Лагранжа

Функцией Лагранжа называется функция

,

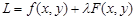где , левая часть уравнения связи (1), а — некоторая постоянная, которая называется множителем Лагранжа. Значение этого множителя определится в процессе нахождения координат точки экстремума.

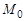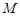Заметим, что условный экстремум функции при условии (1) совпадает с безусловным экстремумом функции Лагранжа, поскольку для точек и , удовлетворяющих условию (1)

.

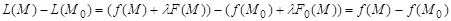Следовательно, из неравенств 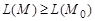, 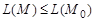следуют неравенства , .

Необходимым условием безусловного экстремума функции Лагранжа является равенство нулю всех ее частных производных первого порядка. Добавляя к этому условию уравнение связи (1), получим систему из трех уравнений с тремя неизвестными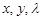

(2)

Решая эту систему, находим координаты возможных точек экстремума и значения множителя . Точки, удовлетворяющие системе (2) называются стационарными точками функции Лагранжа.

Достаточным условием существовании условного экстремума в точке , координаты которой удовлетворяют системе (2), является знакопостоянство второго дифференциала функции Лагранжа при учете условия (1). Из условия (1) следует, что

.

Так как , то из последнего равенства можно выразить через :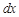

.

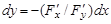Подставляя это соотношение в выражение для второго дифференциала

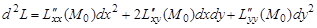
получим

.

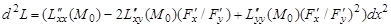Итак, при учете условия связи (1) второй дифференциал принимает вид , где

.

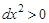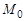Так как при , то знак второго дифференциала совпадает со знаком . Если , то точка является точкой минимума, если 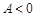, то 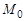— это точка максимума. Если 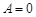, то вопрос о существовании условного экстремума остается открытым. В этом случае нужно проводить дополнительные исследования.

Пример 2. Найти условный экстремум функции двух переменных 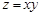при условии, что аргументы этой функции удовлетворяют условию связи .

Запишем функцию Лагранжа

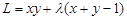
и необходимые условия условного экстремума

,

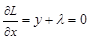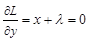, (3)

.

Решая систему (3), определим значение множителя и координаты возможной точки условного экстремума , .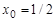

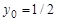Найдем значения вторых производных функции Лагранжа в точке :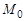

, , .

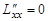Из уравнения связи находим соотношение между дифференциалам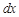и и :

, .

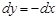Находим второй дифференциал функции Лагранжа, учитывая связь дифференциалов 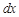и

.

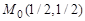Поскольку второй дифференциал функции Лагранжа отрицателен при любых значениях , то точка является точкой условного максимума.

Дата добавления: 2014-01-20