Комплексная форма представления гармонических колебаний

Общие представления о колебательных и волновых процессах. Гармонические колебания. Амплитуда, круговая частота и фаза гармонического колебания. Комплексная форма представления гармонических колебаний. Векторная диаграмма. Свободные колебания. Энергия колебаний. Гармонический осциллятор. Математический, физический и пружинный маятники.

Гармонические колебания и их характеристики.

Кинематика гармонического колебания.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости во времени.

Соответственно, сами эти процессы называются колебательными или периодическими. В зависимости от природы процесса различают механические, электромагнитные, биологические и т.д. колебания. В этом семестре мы с вами будем рассматривать по большей части механические колебания.

Колеблющееся материальное тело, помещённое в упругую среду, будет увлекать за собой и приводить в колебательное движение прилегающие к нему частицы среды, т.е. оно будет являться источником колебаний, распространяющихся от него во все стороны с определённой скоростью. Этот процесс распространения колебаний в упругой среде называется волной..

Изучим основные характеристики колебательных процессов на примере механических колебаний материальной точки. Простейший пример колебаний – изменение со временем координаты вдоль оси 0Х (или оси 0Y) материальной точки D, равномерно вращающейся по окружности (см. рис. 9.1).

Рис. 9.1. Равномерное вращение материальной точки по окружности как пример колебательного процесса.

Материальная точка М, обладающая одной степенью свободы и движущаяся вдоль некоторой линии, может с течением времени сколько угодно удаляться от своего исходного положения – это будет чисто поступательное движение. Колебательным же движением точки М будет называться такое движение, когда точка М не выходит за пределы какого-либо отрезка КL на этой линии и многократно проходит через одни и те же положения внутри отрезка КL.

Колебания называются периодическими, если значения физических величин (или каких-то характерных параметров), описывающих поведение системы, повторяются через равные промежутки времени.

Наименьший промежуток времени Т, в течение которого физические величины, характеризующие колебательный процесс, в точности повторяют свои первоначальные значения, называется периодом колебания.

Простейшими периодическими колебаниями являются гармоническиеколебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса:

S (t) = A сos (ω_ot + φ) = A Sin (ω_ot + φ + π/2) (9.1)

Система, осуществляющая гармонические колебания, называется гармоническим осциллятором.

В уравнении (9.1) величина А, представляющая собой максимальное значение колеблющейся величины, называется амплитудой колебания; величина ω_о называется круговой (циклической) частотой; величина φ - начальной фазой колебания в момент времени t = 0, величина (ω_оt + φ) – фаза колебания в момент времени t.

Частотой колебания υ называется число полных колебаний, совершенных системой за единицу времени (обычно – за 1 секунду):

υ = 1 / Т (9.2)

За промежуток времени, равный периоду колебания Т, фаза колебания получает приращение, равное по величине 2π радиан, так что:

ω_о (t + T) + φ = (ω_оt + φ) + 2π; Т = 2π/ω_о; ω_о = 2πυ (9.3)

Единица частоты – герц (Гц); [Гц] = [с^-1].

Пусть мы имеем гармонически колеблющуюся величину S(t), удовлетворяющую уравнению (9.1).

Тогда:

(9.4)

(9.5)

т.е. имеем гармонические колебания с той же циклической частотой ω_о.

Из уравнений (9.1) и (9.5) можно получить дифференциальное уравнение гармонических колебаний, описывающее колебания гармонического осциллятора:

, (9.6)

где S = А соs (ω_оt + φ) – решение этого дифференциального уравнения.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной системе энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Собственные колебания являются гармоническими.

Векторная диаграмма.

В физике часто используют форму записи колеблющейся величины не через тригонометрические функции синуса или косинуса, а в виде представления через комплексное число с использованием формулы Л. Эйлера для комплексных чисел:

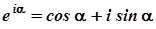, (9.7)

где i=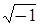 - мнимая единица. Поэтому уравнение гармонического колебания (9.1) можно записать в комплексной форме:

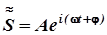(9.8)

Вещественная часть выражения (9.8) описывает гармоническое колебание:

Re (S) = A cos (ω_оt + φ) = S. (9.9)

Обычно обозначение Rе вещественной части комплексного числа в технических текстах опускают и используют упрощенную форму записи:

. (9.10)

В теории колебаний принимается, что колеблющаяся величина S равна вещественной части комплексного выражения, стоящего в равенстве (9.10) справа.

Гармонические колебания можно наглядно представить также с помощью метода вращающегося вектора амплитуды или иначе – метода векторных диаграмм.

Фактически мы уже знакомы с этим методом – вспомним рис 9.1. Для построения векторной диаграммы из произвольной точки О (рис. 9.2), выбранной на оси оХ, под углом φ, равным начальной фазе колебаний откладывается вектор 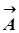, модуль которого равен амплитуде А рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω_о, равной циклической частоте колебаний ω_о, то проекция конца вектора 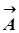будет перемещаться вдоль оси оХ и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону S (t) = А cos (ω_оt + φ).

Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось (например, ось оХ) вектора амплитуды А, отложенного из произвольной точки оси под углом φ, равным начальной фазе колебания, и вращающегося с угловой скорости ω_о вокруг этой точки. Такой метод называется методом векторных диаграмм.

Рис. 9.2. Метод векторных диаграмм для графического изображения гармонических колебаний.

Свободные колебания. Энергия колебаний.

Гармонический осциллятор.

Мы уже записывали, что свободные колебания – это разновидность гармонических колебаний системы, которые совершают за счет первоначально сообщенной системе энергии при последующем отсутствии внешних воздействий на колебательную систему, т.е. в отсутствие потерь энергии.

Теперь мы выясним, какими силами вызываются гармонические колебания, воспользовавшись для этого законами динамики. Пусть материальная точка массой m совершает прямолинейные гармонические колебания вдоль оси координат оХ около положения равновесия, принятого за начало координат. Тогда зависимость координаты Х от времени t задается уравнением, аналогичным уравнению (9.1):

Х (t) = А cos (ω_оt + φ). (9.11)

Скорость V (t) и ускорение а (t) колеблющейся материальной точки в любой момент времени будут соответственно задаваться уравнениями:

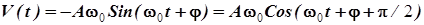(9.12)

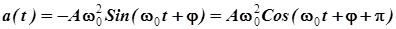(9.13)

В соответствии со 2-м законом Ньютона, на колеблющуюся материальную точку массой m будет действовать сила, по модулю равная F = ma:

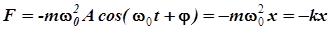. (9.14)

Следовательно, при гармонических колебаниях сила пропорциональна смещению материальной точки от положения равновесия и направлена в противоположную сторону (к положению равновесия). Такого рода силы называются квазиупругими (или упругими, если имеют место колебания тела под действием упругих деформаций подвеса материальной точки).

Рассмотрим теперь энергетику гармонических колебаний материальной точки, колеблющейся под действием упругой или квазиупругой силы, подчиняющейся закону F(х) = ─kх.

Кинетическую энергию материальной точки найдём из соотношения:

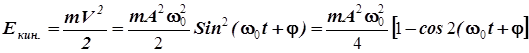. (9.15)

Из выражения (9.15) видим, что кинетическая энергия материальной точки осциллирует со временем с удвоенной частотой по сравнению с частотой её колебаний ω_о.

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы из положения равновесия до некоторого положения Х на оси ординат, может быть найдена интегрированием:

=

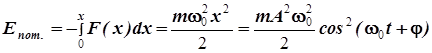= . (9.16)

- видим, что и потенциальная энергия колеблющейся материальной точки осциллирует с частотой 2ω_о, вдвое превышающей частоту колебаний точки.

Полная энергия материальной точки, совершающей гармонические колебания, может быть найдена из уравнений (9.15) и (9.16):

..(9.17)

При гармонических колебаниях полная энергия системы остаётся постоянной, поскольку квазиупругие силы являются консервативными, для которых справедлив закон сохранения полной механической энергии.

Дата добавления: 2014-01-20