Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля

Диск

При размещении между источником S ₀ и экраном круглого непрозрачного диска CB закрывается одна или несколько первых зон Френеля. Если диск закроет m зон Френеля, то в точке Р амплитуда суммарной волны:

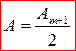(9)

Таким образом, в случае круглого непрозрачного диска в цент­ре картины (точка Р) при любом (как четном, так и нечетном) m получается светлое пятно.

Если диск закрывает много зон Френеля, интен­сивность света в области геометрической тени практически всюду равна нулю и лишь вблизи границ наблюдается слабая интерференционная картина. В этом случае можно пренебречь явлением дифракции и пользоваться законом прямолинейного распространения света.

Дифракцией света называется явление отклонения света от прямолинейного распространения, когда свет, огибая препятствие, заходит в область геометрической тени.

Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией.

Наблюдение дифракции можно осуществить, если на пути световой волны поместить непрозрачную преграду с отверстием, размеры которого соизмеримы с l (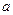~) (рис. 1а). На экране, расположенном за преградой, будет наблюдаться световое пятно с рядом темных и светлых колец, значительно превышающее размеры геометрической тени (г.т.) отверстия на экране. Если 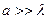, выполняются законы геометрической оптики (рис. 1б).

Различают два вида дифракции:

1) дифракция Фраунгофера (дифракция в параллельных лучах) – если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие и идущие в точку наблюдения, образуют практически параллельный пучок;

2) дифракция Френеля – если данное условие не выполняется.

Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса. Принцип Гюйгенса позволяет решать задачи о распространении волнового фронта (рис. 2), но не отвечает на вопрос об интенсивности волн, идущих по различным направлениям. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства.

Развитый таким образом принцип получил название принципа Гюйгенса-Френеля.

Принцип Гюйгенса-Френеля: каждая точка фронта волны является источником когерентных вторичных сферических волн, интерференция которых определяет результирующую волну в следующий момент времени. Амплитуда вторичной сферической волны пропорциональна величине площади волновой поверхности, излучающей эту волну. Максимум излучения вторичных волн происходит в направлении нормали к волновой поверхности.

В общем случае нахождение амплитуды результирующего колебания представляет собой сложную задачу. Однако, как показал Френель, в случаях, обладающих симметрией, нахождение амплитуды результирующего колебания может быть осуществлено более простым методом, разработанным Френелем и получившим название метода зон Френеля.

Определим методом Френеля амплитуду светового колебания, возбуждаемого в точке М сферической волной, распространяющейся в изотропной однородной среде из точечного источника S (рис. 3). Действие источника света S заменяется действием вспомогательных источников, расположенных на одной из волновых (любой) поверхностей S’. Поверхность S’ разбивается на кольцевые зоны Френеля таким образом, чтобы расстояния от границ зоны до точки М отличались на l/2. Если расстояние от волновой поверхности S’ до точки М равно r₀, то для построения зон проводятся из точки М сферы радиусами

.

Пересечение этих сфер с волновой поверхностью S’ определяет границы зон Френеля, выделяемых на этой поверхности. Вычисление площади этих зон показывает, что площади всех зон Френеля примерно одинаковы.

Окончательный результат получается сложением действий каждой зоны в точке М, причем учитывается, что:

1) действие соседних зон ослабляет друг друга, т.к. эти зоны посылают в точку М колебания в противофазе;

2) действие зоны уменьшается с увеличением угла между нормалью к поверхности зоны и направлением на точку М.

Поэтому амплитуды колебаний А₁, А₂…, создаваемые первой, второй и т.д. зонами в точке М, связаны неравенствами:

А₁>А₂> А₃…

Амплитуда результирующего колебания в точке М может быть представлена в виде

А =А₁ – А₂ + А₃ – А₄ +…

Все амплитуды от нечётных зон входят с одним знаком, а от чётных зон – с другим.

Запишем это уравнение в виде

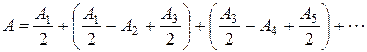
Вследствие монотонного убывания А_m можно приближённо считать, что

Тогда выражения в скобках будут равны нулю,

.

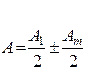
Амплитуда, создаваемая в точке М всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, если число зон велико и А_m – ничтожно мало.

Если в некотором отверстии, до которого дошел фронт волны, поместится четное число зон Френеля, в точке М будет наблюдаться темное пятно, окруженное чередующимися световыми и темными кольцами. Если в отверстии помещается нечетное число зон Френеля, в точке М будет светлое пятно.

Если на пути световой волны поставить зонную пластинку, которая бы перекрывала все четные или нечетные зоны, то интенсивность света в точке М резко возрастет.

Метод зон Френеля позволяет решить ряд практических задач на дифракцию света.

Дата добавления: 2014-01-20