
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 3. “ Плоское движение твердого тела”
|
|
|
|
Лекция № 5–6
§ 1. Плоскопараллельное движение твердого тела. Уравнения плоского движения тела.
Определение. Плоскопараллельным (плоским) движением тела называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой фиксированной плоскости, которая называется направляющей или базовой.
 Рис. 24
Рис. 24
| Плоское движение твёрдого тела имеет большое значение в технике, т. к. звенья большинства механизмов и машин, применяемых в технике, совершают плоское движение. Пусть твёрдое тело совершает плоское движение, параллельное неподвижной плоскости П0. Тогда любая прямая, перпендикулярная этой плоскости и жестко скрепленная своими точками с движущимся телом, будет двигаться поступательно, т.е. все точки этой прямой движутся одинаково. | ||
 Рис. 25
Рис. 25
| Доказать это можно таким образом. Выберем в теле 4 точки A,B,C,D так, чтобы точки A,B,C находились в плоскости и не лежали на одной прямой, а точка D размещалась вне этой плоскости. Пирамида, построенная на этих точках, движется так, что её основание всё время находится в фиксированной плоскости. Тогда её высота, проведенная через т. D, перемещается параллельно сама себе. Т. о., при изучении плоского движения достаточно изучить движение | ||
какого–нибудь сечения тела, которое параллельно направляющей плоскости.
Движение этого сечения определяется движением трёх его точек, не лежащих на одной прямой. Из 6 параметров, определяющих движение этих точек, независимыми будут только три, т. к.

Следовательно, при плоскопараллельном движении тело имеет три степени свободы. Выберем соответствующие параметры, определяющие движение тела.
|
|
|
 Рис. 26
Рис. 26
| Зададим координаты произвольной точки А, как функции времени:
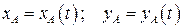 .
Назовем эту точку полюсом. Движение точки А определяет движение прямой, проходящей через точку А перпендикулярно к плоскости сечения.
Если теперь задать угол поворота тела вокруг этой прямой .
Назовем эту точку полюсом. Движение точки А определяет движение прямой, проходящей через точку А перпендикулярно к плоскости сечения.
Если теперь задать угол поворота тела вокруг этой прямой 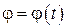 , то движение тела будет определено. Угол этот отсчитывается от некоторой фиксированной прямой , то движение тела будет определено. Угол этот отсчитывается от некоторой фиксированной прямой  до прямой до прямой 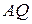 , жестко связанной с сечением. , жестко связанной с сечением.
|
Положительное направление отсчета угла показано на рис. 26.
Таким образом, уравнения плоскопараллельного движения имеют вид:
 (3.1)
(3.1)
§ 2. Скорость точек тела при его плоскопараллельном движении. Формула Эйлера. Теорема о проекциях скоростей.
Любое движение твёрдого тела, в том числе и плоское движение, бесчисленным множеством способов можно разложить на два движения: переносное и относительное. Примем за переносное движение фигуры её движение вместе с поступательно движущейся системой координат  , связанную с полюсом А. Тогда относительное движение фигуры будет по отношению к подвижной системе координат
, связанную с полюсом А. Тогда относительное движение фигуры будет по отношению к подвижной системе координат  вращением вокруг неподвижной оси, проходящей через полюс перпендикулярно плоскости фигуры.
вращением вокруг неподвижной оси, проходящей через полюс перпендикулярно плоскости фигуры.
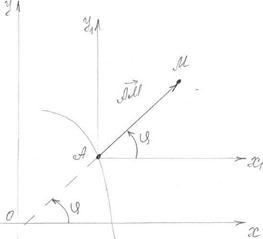 Рис. 27
Рис. 27
| Абсолютную скорость точки М можно определить согласно теореме о сложении скоростей:
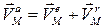 , где , где
 . .
 – угловая скорость тела при его вращении вокруг указанной оси.
Тогда абсолютная скорость точки М будет равна: – угловая скорость тела при его вращении вокруг указанной оси.
Тогда абсолютная скорость точки М будет равна:
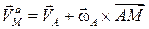 (3.2) (3.2)
|
Возникает вопрос: как меняется угловая скорость тела при выборе полюса в другой точке?
Теорема: Угловая скорость тела не зависит от выбора полюса.
Доказательство: Рассмотрим сечение тела. Выберем полюса в точках А и В.
 Рис. 28
Рис. 28
| На основании (3.2) запишем скорость точки М:
 Но скорость самой точки В относительно полюса А определяется формулой:
Но скорость самой точки В относительно полюса А определяется формулой:
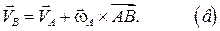 Вычтем из (а) (в):
Вычтем из (а) (в):

|
а из (б)  .
.
Т. к. левые части уравнений равны, то равны и правые, т.е.  или
или  .
.
Т. к. вектор  произволен, то равняться нулю может лишь выражение в скобках, т.е.
произволен, то равняться нулю может лишь выражение в скобках, т.е. . ■
. ■
|
|
|
Итак, скорость любой точки при плоскопараллельном движении равна:
 (3.3)
(3.3)
Эта формула принадлежит Эйлеру и носит его имя.
Угловая скорость тела при плоскопараллельном движении направлена перпендикулярно плоскости сечения тела в сторону, откуда поворот тела видно против движения стрелки часов, и проекция её на ось z равна 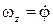 .
.
Разность скоростей двух точек твердого тела VМ и VА представляет собой добавку VМА к скорости VА точки А (полюса), необходимую, чтобы получить скорость VМ точки М:
 . (3.4)
. (3.4)
Будем называть эту добавку VМА дополнительной скоростью точки М по отношению к полюсу А.
Проектируя формулу Эйлера (3.3) на направленный отрезок 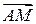 , получим
, получим

Так как векторное произведение  есть вектор, ортогональный вектору
есть вектор, ортогональный вектору 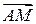 , то его проекция на направление указанного вектора равна нулю. Поэтому имеем
, то его проекция на направление указанного вектора равна нулю. Поэтому имеем
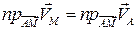 . (3.5)
. (3.5)
Равенство (3.5) выражает теорему, впервые полученную Эйлером.
Теорема: Проекции скоростей двух точек твердого тела на направленный отрезок, их соединяющий, равны.
Теорема Эйлера отражает то требование, которое налагает нараспределение скоростей точек тела неизменность расстояний между ними. Если разложить скорости точек А и М на составляющие, коллинеарные отрезку 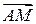 и ортогональные ему, то составляющие скоростей двух точек
и ортогональные ему, то составляющие скоростей двух точек  и
и (рис. 29), направленные вдоль отрезка
(рис. 29), направленные вдоль отрезка 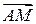 , должны быть направлены в одну сторону и иметь одинаковые величины. Если бы величина вектора
, должны быть направлены в одну сторону и иметь одинаковые величины. Если бы величина вектора  была больше величины вектора
была больше величины вектора  , то точка А, сближалась бы с точкой М; если же величина
, то точка А, сближалась бы с точкой М; если же величина  была бы больше
была бы больше  , то точки А и М удалялись бы друг от друга. Разумеется, эти утверждения верны для случая, когда
, то точки А и М удалялись бы друг от друга. Разумеется, эти утверждения верны для случая, когда и
и 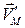 направлены в ту же сторону, что и вектор
направлены в ту же сторону, что и вектор 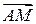 , если же обе они направлены и сторону, противоположную отрезку АМ, т. е. в сторону отрезка
, если же обе они направлены и сторону, противоположную отрезку АМ, т. е. в сторону отрезка 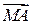 , то в первом случае точки будут удаляться друг от друга, во втором будут сближаться. Все эти случаи не могут иметь место вследствие неизменности расстояний между точками А и М. На ортогональные отрезку АМ составляющие скоростей
, то в первом случае точки будут удаляться друг от друга, во втором будут сближаться. Все эти случаи не могут иметь место вследствие неизменности расстояний между точками А и М. На ортогональные отрезку АМ составляющие скоростей  и
и  неизменность расстояний между точками никаких ограничений ни на их величину, ни на их направление не налагает, так что они могут быть направлены либо в одну и ту же сторону, либо в противоположные стороны и могут иметь произвольные величины.
неизменность расстояний между точками никаких ограничений ни на их величину, ни на их направление не налагает, так что они могут быть направлены либо в одну и ту же сторону, либо в противоположные стороны и могут иметь произвольные величины.
|
|
|
Из теоремы Эйлера вытекают следствия:
1) если скорости двух точек твердого тела параллельны и перпендикулярны отрезку, их соединяющему, то они равны;
2) если проекция скорости какой–либо точки отрезка на отрезок
равна нулю, то скорости других точек этого отрезка либо равны
нулю, либо перпендикулярны отрезку.
Справедлива также теорема, в некотором смысле обратная теореме Эйлера.
Теорема. Если проекции скоростей двух точек на направленный отрезок, их соединяющий, равны на протяжении некоторого промежутка времени, то расстояние между этими точками остается постоянным.
§ 3. Графическое распределение скоростей точек тела. МЦС и способы его нахождения.
Рассмотрим произвольную прямую сечения, которая перпендикулярна скорости точки А.
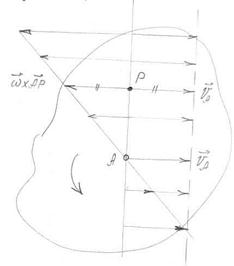 Рис. 30
Рис. 30
| Векторы  и и  для точек этой прямой параллельны между собой и для верхнего от точки А луча направлены в противоположные стороны, а для нижнего луча – в одну сторону. На верхнем луче возможна такая точка Р, для которой для точек этой прямой параллельны между собой и для верхнего от точки А луча направлены в противоположные стороны, а для нижнего луча – в одну сторону. На верхнем луче возможна такая точка Р, для которой  и и  равны по величине противоположны по направлению. Значит, их сумма равна нулю: равны по величине противоположны по направлению. Значит, их сумма равна нулю: 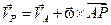 .
Точка Р расположена на верхнем луче АР, который можно получить поворотом скорости точки А в сторону вращения на 90°.
Расстояние АР находится из равенства: .
Точка Р расположена на верхнем луче АР, который можно получить поворотом скорости точки А в сторону вращения на 90°.
Расстояние АР находится из равенства:  . .
|
Определение. Точка Р, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).
Если МЦС существует, то эту точку целесообразно выбрать в качестве полюса. Тогда формула Эйлера упрощается: , но возникает вопрос: как найти мгновенный центр скоростей?
, но возникает вопрос: как найти мгновенный центр скоростей?
Методы нахождения МЦС.
 Рис. 31
Рис. 31
| 1. Если известны  и и 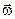 , то для нахождения МЦС необходимо повернуть вектор , то для нахождения МЦС необходимо повернуть вектор в сторону вращения тела на 90° и на найденном луче отложить отрезок АР, который равен: в сторону вращения тела на 90° и на найденном луче отложить отрезок АР, который равен: 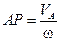 . .
| ||
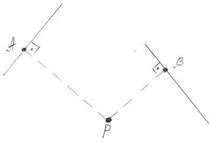 Рис. 32
Рис. 32
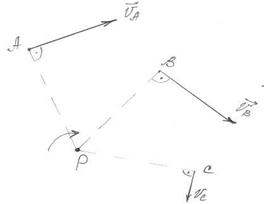
| 2. Если известны направления скоростей двух точек тела и их направления не коллинеарны, то МЦС находится в точке пересечения перпендикуляров, проведенных к скоростям в указанных точках. | ||
3. Если скорости двух точек тела параллельны и ^ отрезку, соединяющему точки, то МЦС находится в точке пересечения этой прямой и прямой, соединяющей концы векторов скоростей.
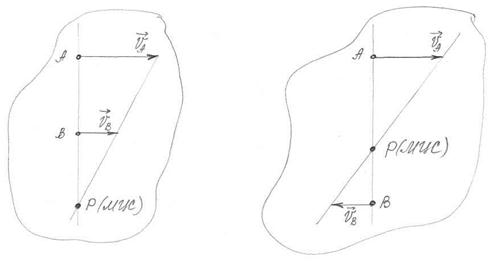 Рис. 33
Рис. 33
| |||
Исключения из правил 2 и 3.
|
|
|
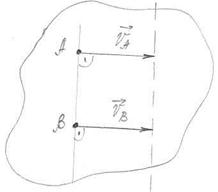
2 а). Если направления скоростей  и и 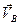 параллельны, то перпендикуляры к скоростям не пересекаются. параллельны, то перпендикуляры к скоростям не пересекаются.
 Рис. 34
Рис. 34
| 3 а). Если  = =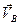 , то МЦС не существует. , то МЦС не существует.
| ||
 Рис. 35
Рис. 35
| 4. Если колесо катится без скольжения по неподвижной поверхности, то МЦС находится в точке касания колеса и неподвижной поверхности. | ||
Рекомендации к решению задач.
1. Величины скоростей пропорциональны расстояниям от точек до МЦС: 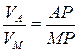 ,
,
 т.е. для того, чтобы определить скорость любой точки тела необходимо знать скорость какой–нибудь одной его точки и положение МЦС.
т.е. для того, чтобы определить скорость любой точки тела необходимо знать скорость какой–нибудь одной его точки и положение МЦС.
2. Чтобы найти направление скорости любой точки тела, необходимо соединить её с МЦС и провести перпендикуляр к этому отрезку в сторону вращения тела. Обратить внимание на то, что ориентация скоростей всех точек тела должна быть одинаковой.
|
§ 4. Ускорения точек тела при плоскопараллельном движении.
По определению 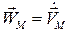 , тогда
, тогда 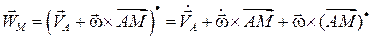 .
.
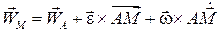 (3.6)
(3.6)
Найдем 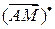 .
.
 Рис. 37
Рис. 37
| Из рисунка имеем 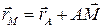 . Продифференцируем это выражение один раз по времени: . Продифференцируем это выражение один раз по времени: 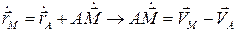 .
Однако, согласно формуле Эйлера .
Однако, согласно формуле Эйлера 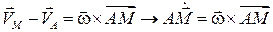 . .
|
Тогда 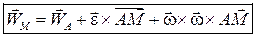 . (3.7)
. (3.7)
Эта формула носит имя Ривальса.
Обозначим 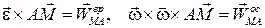 . Тогда формула Ривальса примет вид:
. Тогда формула Ривальса примет вид: 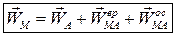 . (3.8)
. (3.8)
Вычислим величины и направления векторов, входящих в (3.8).
Величина и направление  определяется тем, что
определяется тем, что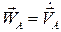 . Величина вращательного ускорения точки М относительно полюса А
. Величина вращательного ускорения точки М относительно полюса А
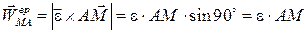 . (3.9)
. (3.9)
Направление 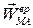 определяется пот правилам векторного произведения.
определяется пот правилам векторного произведения.
Величина осестремительного ускорения точки М относительно полюса А равна: 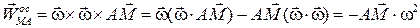 .
.
Тогда  . (3.10)
. (3.10)
Вектор 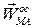 направлен вдоль линии
направлен вдоль линии 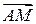 от точки М к полюсу А.
от точки М к полюсу А.
Тогда, окончательно, формула Ривальса примет вид:
 . (3.11)
. (3.11)
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 833; Нарушение авторских прав?; Мы поможем в написании вашей работы!