Установление функциональных связей (ФС) между объектами

УСТАНОВЛЕНИЕ СВЯЗЕЙ МЕЖДУ ОБЪЕКТАМИ В ИНФОРМАЦИОННОЙ СИСТЕМЕ

Запросы к информационной базе данных должны быть определены и сформулированы еще до определения структурных связей между объектами. Первоначально запросы формулируются заказчиком. Проектировщик анализирует каждый запрос и при необходимости видоизменяет его. После этого согласовывает с заказчиком. Например, первоначально запрос имел вид: определить номенклатуру предприятия с указанием используемых материалов. После видоизменения проектировщиком запрос имеет вид: для данного предприятия выдать список его изделий с указанием для каждого изделия используемых материалов. Каждому запросу сопоставляется совокупность ФС. При этом ФС представляет собой элемент алгоритма информационного поиска. Отметим, что ФС указывает лишь на последовательность выбора экземпляров объекта для обработки запроса. Обозначим ФС следующим образом

где А_1, А_2…, А_m – исходные объекты,

В_1, В_2,… В_n, -конечные объекты.

Если исходный объект один, то это одномерная ФС, в другом случае – многомерная.

Под последовательностью ФС будем понимать упорядоченную совокупность, в которой всякое n-ная ФС используется в качестве исходного конечного объекта m-той ФС, 1≤m<n.

Для начала выполнения исследования необходимо обратится к экземплярам исходных объектов первой ФС. Для таких объектов задается характеристика В6, которая определяет дополнительные способы обращения к экземплярам объектов. В6 может принимать следующие значения:

D непосредственное обращение к экземплярам объектов,

В6 = S последовательное обращение к экземплярам объектов, DS обеспечение обеих возможностей.

Значение характеристики В6 определяется из текста запроса. Например, если имя в запросе обозначено словом «данному» или «указанному», в этом случае В6 = D. Если слово «каждому», то В6 = S.

В большинстве ФС используется один конечный объект. Однако, как видно из определения ФС, в не могут участвовать и несколько конечных объектов. В этом случае совокупность всех конечных объектов представляется как один объект.

Например, имеем запрос: указать список всех жильцов данного дома (служащие, студенты, пенсионеры и т.д.). Отсюда видно, что указанные в скобках объекты можно условно объединить в один объект – жилец или квартиросъемщик. ФС здесь порождается таким запросом:

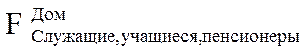
Как указывалось выше, существует четыре типа связей между объектами: 1:1, 1:М, М:1, М:N. Тип соответствия между объектами будем обозначать Т (А,В). Например, тип соответствия

Т (предприятие, изделие)=M:N

Если последовательность ФС состоит только из одномерных связей, то ее преобразовывать не нужно. Если же в последовательности определены многомерные ФС, то эти связи требуется преобразовать к более простым. Введем некоторые определения:

1. Две совокупности ФС F_1,, F₂, …, F_k, F_1,, F₂, …, F_k называются тождественными, если результаты их выполнения, полученные на одних и тех же экземплярах объектов, заданных в запросе, совпадают.

Пример. Дан запрос: выдать список всех учеников данной школы посещающих указанную библиотеку. Этому запросу соответствуют две тождественные последовательности:

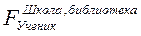ºº

Необходимо отметить, что порядок расположения исходных объектов в многомерной ФС можно менять, получая при этом тождественную ФС.

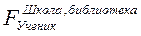º

2. Упорядоченная совокупность объектов A₁,…, А_k называется цепью объектов для " I, 1≤i<(k-1), если для "_i выполняется

T(A_i,, A_i+1)=1:М

Пример. Университет, факультет, студент.

3. Упорядоченная совокупность ФС вида

,

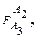называется цепью ФС, если совокупность A_{1, ……}A_k является цепью объектов. Процесс преобразования последовательности ФС заключается в замене этой последовательности на тождественную.

Преобразования последовательностей ФС

Преобразование 1.

Если среди исходных объектов многомерной ФС

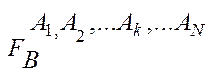(1)

Можно выделить цепь объектов A_1, A_{2, ……}A_k, то такой многомерной ФС можно поставить в соответствие тождественную совокупность ФС:

º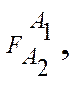

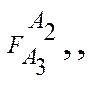
Для выделения цепи исходных объектов сопоставляются таблицы типов соответствия.

Пример. Для четырех исходных объектов можно задать таблицу.

Исходный объект	A2	A3	A4	Если хотя бы в одной клетке таблицы задан тип соответствия, который отличается от M:N, то среди исходных объектов всегда можно выделить цепь.
A1	Т(A1,A2)	Т(A1,A3)	Т(A1, A4)
	A2	Т(A2,A3)	Т(A2, A4)
		A3	Т(A3, A4)

Например, задан запрос: для заданного отделения свя зи названного района и города необходимо выделить список адресатов, получающих указанное подписное издание.

F=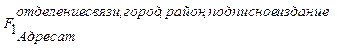

Исходный объект	Город	Район	Подписное издание
Отделение связи	М:1	М:1	M:N
	Город	1:М	M:N
		Район	M:N

В соответствии с указанной выше рекомендацией запишем следующее соответствие:

F== F₂

Отметим, что во второй ФС имеет место цепь исходных объектов город, район, отделение связи, для которых выполняется преобразование:

F₂º ,,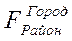

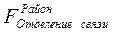Примечание 1. Поскольку объекты: город, район, отделение связи образуют цепь, то отделение связи однозначно определяет город и район. Следовательно, информация о городе и районе необходима только для обращения к искомому отделению связи, т.е. к экземпляру соответствующего объекта.

Примечание 2. Если в результате преобразований выделяется цепь ФС

,

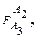а в соответствующей цепи исходных событий есть объект A_i, 1≤i≤k для которого характер В6=D(DS), т.е. имеется возможность обращения к экземпляру объекта по назначению идентификатора, то в этих случаях первоначально определенная цепь ФС должна быть упразднена, если i=k и усечена, если i<k до следующего вида:

Например, рассмотренная выше последовательность ФС может быть представлена в виде:

(2)

Преобразование 2.

A_i, A_2,…, A_N

Если среди исходных объектов многомерной ФС F_в существует объект, для которого тип соответствия Т(А,В)=1:М, то такой многомерной связи сопоставляется тождественная совокупность ФС:

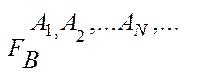º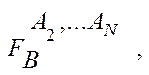

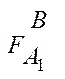
Если же первоначально ФС содержит только два исходных объекта, то ей можно сопоставить одну их двух тождественных совокупностей.

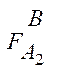ºº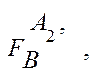

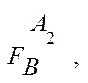
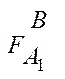
Возьмем ФС из выражения (2). Проанализируем эту связь. Очевидно, что тип связи

Т (подписное издание, адресат)= M:N,

Т (отделение связи, адресат)= 1:М.

Следовательно, можно провести следующее тождественное преобразование:

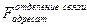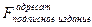º,º,

Отметим, что если в результате выполненных преобразований получена много мерная ФС, которая в дальнейшем уже не может быть подвергнута преобразованиям, то тип соответствия между объектами равен M:N. В то же время тип соответствия между любым исходным и конечным объектом не равен 1:М. Такая многомерная ФС называется канонической. Любая одномерная ФС является канонической.

3. Пусть одна многомерная ФС ,

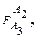Тогда упорядоченная совокупность ФС следующего вида 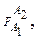будем называть обратной

поотношениюкзаданнойФС.

Преобразование 3.

Если в процессе преобразования некоторой многомерной ФС было выделено более одной цепи исходных объектов, то окончательно в последовательности ФС должна быть сохранена лишь одна из этих цепей. Все остальные цепи заменяются обратными совокупностями.

Следует отметить, что после второго преобразования проводится проверка: входит ли объект A_i, для которого определена ФС типа F^B в цепь исходных объектов или не входит. A_i

Если входит, то соответствующая этой цепи объектов цепь ФС заменяется обратной совокупностью связей. На этапе описания и анализа ФС определяется значение характеристики В7, которая носит название структурной активности.

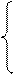А

В7=

N

Если В7=А, то при последующем развитии базы для этого объекта могут определяться новые ФС, следовательно он может входить в новые структурные связи.

При В7=N, предполагается, что объект не будет менять свой статус в информационной базе.

Дата добавления: 2014-01-20