
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Суммы Дарбу
|
|
|
|
В качестве вспомогательного средства исследования, наряду с интегральными суммами, введём в рассмотрение так называемые суммы Дарбу. Обозначим через 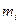 и
и 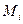 , соответственно, точные нижнюю и верхнюю границы функции
, соответственно, точные нижнюю и верхнюю границы функции 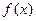 в
в 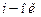 промежутке
промежутке  и составим суммы:
и составим суммы:
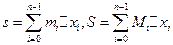
Эти суммы называются, соответственно, нижней и верхней интегральными суммами Дарбу.
В частном случае, когда 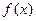 непрерывна, они являются просто наименьшей и наибольшей из интегральных сумм, отвечающих взятому разбиению, так как в этом случае функция
непрерывна, они являются просто наименьшей и наибольшей из интегральных сумм, отвечающих взятому разбиению, так как в этом случае функция 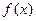 в каждом промежутке достигает своих границ, и точки
в каждом промежутке достигает своих границ, и точки 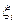 можно выбрать так, чтобы было
можно выбрать так, чтобы было 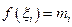 или
или 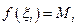
Пере6ходя к общему случаю, из самого определения нижней и верхней границ, имеем: 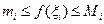 . Умножив это неравенство на
. Умножив это неравенство на 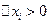 и просуммировав по
и просуммировав по 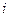 , получим:
, получим:
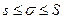 .
.
При фиксированном разбиении суммы s и S будут постоянными, в то время как сумма 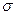 ещё остаётся переменной ввиду производности чисел
ещё остаётся переменной ввиду производности чисел 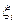 . Но за счёт выбора
. Но за счёт выбора 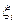 можно значения
можно значения 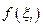 сделать сколь угодно близкими как к
сделать сколь угодно близкими как к 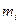 , так и к
, так и к 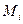 , а значит – сумму
, а значит – сумму 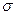 сделать сколь угодно близкой к s или к S. А тогда предыдущие неравенства приводят к следующему общему замечанию: при данном разбиении промежутка, суммы Дарбу s и S служат точными, соответственно, нижней и верхней границами для интегральных сумм.
сделать сколь угодно близкой к s или к S. А тогда предыдущие неравенства приводят к следующему общему замечанию: при данном разбиении промежутка, суммы Дарбу s и S служат точными, соответственно, нижней и верхней границами для интегральных сумм.
Суммы Дарбу обладают следующими свойствами:
I.Если к имеющимся точкам деления добавить новые точки, то нижняя сумма Дарбу может от этого разве лишь возрасти, а верхняя сумма – разве лишь уменьшиться.
Доказательство:
Для доказательства этого свойства достаточно ограничиться присоединением к уже имеющимся точкам деления ещё одной точки 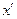 . Пусть
. Пусть 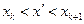 .
.
Если 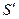 обозначить новую верхнюю сумму, то от прежней S она будет отличаться только тем, что в сумме S промежутку
обозначить новую верхнюю сумму, то от прежней S она будет отличаться только тем, что в сумме S промежутку 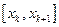 отвечало слагаемое
отвечало слагаемое 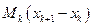 , а в новой сумме
, а в новой сумме 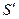 этому промежутку отвечает сумма двух слагаемых
этому промежутку отвечает сумма двух слагаемых 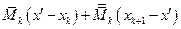 , где
, где 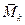 и
и 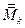 есть точные верхние границы функции
есть точные верхние границы функции 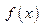 в промежутках
в промежутках 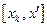 и
и  . Так как эти промежутки являются частями промежутка
. Так как эти промежутки являются частями промежутка 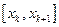 , то
, то
|
|
|
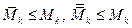
так что
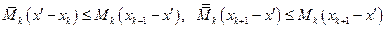
Складывая эти неравенства, получаем:
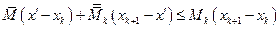
Отсюда и следует, что
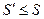
Для нижней суммы доказательство аналогично.
Ч.т.д.
II.Каждая нижняя сумма Дарбу не превосходит верхней суммы, хотя бы отвечающей и другому разбиению промежутка.
Доказательство:
Разобьём промежуток  произвольным образом на части и составим для этого разбиения суммы Дарбу
произвольным образом на части и составим для этого разбиения суммы Дарбу 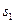 и
и 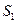 . Рассмотрим теперь некоторые другие разбиения промежутка
. Рассмотрим теперь некоторые другие разбиения промежутка  . Ему будут отвечать суммы
. Ему будут отвечать суммы 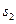 и
и 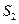 . Требуется доказать, что
. Требуется доказать, что 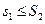 . С этой целью объединим те и другие точки деления; тогда получим некоторое третье, вспомогательное разбиение, которому будут отвечать суммы
. С этой целью объединим те и другие точки деления; тогда получим некоторое третье, вспомогательное разбиение, которому будут отвечать суммы 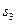 и
и 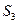 .
.
Третье разбиение получено из первого добавлением новых точек деления; поэтому, на основании свойства 1) сумм Дарбу, имеем 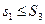 (обе нижние суммы!)
(обе нижние суммы!)
Составив теперь второе и третье разбиения, точно так же заключаем, что 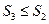 . Но
. Но 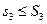 , так что из только что полученных неравенств вытекает:
, так что из только что полученных неравенств вытекает:
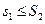 .
.
Ч.т.д.
Замечание. Из доказанного, следует, что всё множество 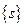 нижних сумм ограничено сверху, например, любой верхней суммой
нижних сумм ограничено сверху, например, любой верхней суммой 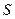 . В таком случае, это множество имеет конечную точную верхнюю границу:
. В таком случае, это множество имеет конечную точную верхнюю границу:  , и, кроме того,
, и, кроме того, 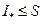 , какова бы ни была верхняя сумма
, какова бы ни была верхняя сумма 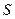 . При этом множество
. При этом множество 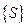 верхних сумм оказывается ограниченным снизу числом
верхних сумм оказывается ограниченным снизу числом 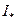 Следовательно, оно имеет точную нижнюю границу:
Следовательно, оно имеет точную нижнюю границу: 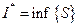 , получим, очевидно,
, получим, очевидно, 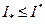 .
.
Сопоставляя всё сказанное, имеем:
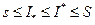 ,(4)
,(4)
Для любых 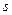 и
и 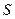 .
.
Числа 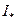 и
и 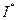 называются, соответственно, нижним и верхним интегралами Дарбу.
называются, соответственно, нижним и верхним интегралами Дарбу.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1107; Нарушение авторских прав?; Мы поможем в написании вашей работы!