
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы интегрирования
|
|
|
|
К основным методам интегрирования относятся: метод замены переменной и метод интегрирования по частям.
Метод замены переменной (метод подстановки)
1. Метод подведения по знак дифференциала – частный случай метода замены переменной. Данный метод прост и применяется в большом количестве интегралов.
В основе данного метода лежит свойство инвариантности формул интегрирования, которое гласит: если 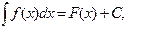 то
то 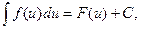 где
где  произвольная дифференцируемая функция от x.
произвольная дифференцируемая функция от x.
Рассмотрим один из табличных интегралов  По свойству 6 эта формула остается справедливой не только в случае, когда x –независимая переменная, но и тогда, когда вместо x стоит некоторая дифференцируемая функция. Например,
По свойству 6 эта формула остается справедливой не только в случае, когда x –независимая переменная, но и тогда, когда вместо x стоит некоторая дифференцируемая функция. Например, 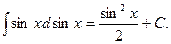
Аналогичная ситуация имеет место и для других формул:
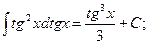

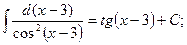

Пример 7.3. Вычислить интеграл 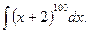
Решение. Что мешает применить степенной интеграл (1) для 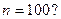 Понятно, что если бы под знаком дифференциала стояло выражение
Понятно, что если бы под знаком дифференциала стояло выражение 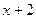 , а не x, то такой интеграл был бы табличным. Вопрос: возможно ли заменить
, а не x, то такой интеграл был бы табличным. Вопрос: возможно ли заменить  на
на  Ответ – да, по свойству дифференциала:
Ответ – да, по свойству дифференциала: 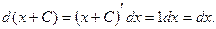 На основании этого свойства
На основании этого свойства 
Значит, 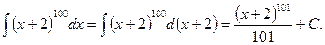
Пример 7.4. Вычислить интеграл 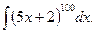
Решение. Для применения табличной формулы степенного интеграла при 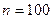 необходимо, чтобы под знаком дифференциала стояло выражение
необходимо, чтобы под знаком дифференциала стояло выражение 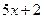 вместо x. Вопрос: возможно ли заменить
вместо x. Вопрос: возможно ли заменить  на
на  Ответ– да, по свойству дифференциала:
Ответ– да, по свойству дифференциала: 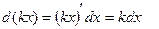 или
или 
На основании свойств дифференциала 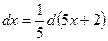 . Следовательно
. Следовательно  В рассмотренных выше примерах дифференциал изменялся на основании его свойств, т.е. вместо
В рассмотренных выше примерах дифференциал изменялся на основании его свойств, т.е. вместо 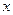 под знак дифференциала подводилась некоторая линейная функция вида
под знак дифференциала подводилась некоторая линейная функция вида 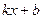 , где
, где 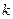 и
и 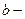 некоторые числа, причем
некоторые числа, причем 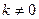 . Обобщим это в виде теоремы.
. Обобщим это в виде теоремы.
Теорема 8.2. Пусть  одна из первообразных для
одна из первообразных для 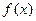 . Тогда
. Тогда  где
где 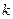 и
и 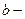 некоторые числа, причем
некоторые числа, причем 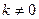 .
.
|
|
|
Доказательство. Для доказательства равенства возьмем производную от правой части формулы(..) и покажем, что она равна подынтегральной функции:
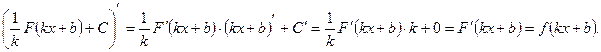 Теорема доказана.
Теорема доказана.
При сведении интеграла к табличному часто используются следующие преобразования дифференциала – «подведение под знак дифференциала».
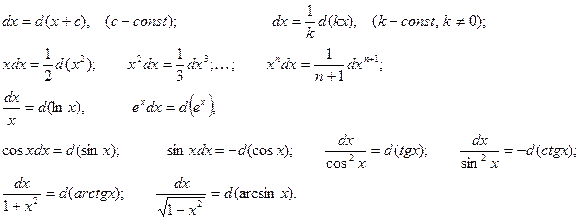
Пример 8.1. Найти интегралы а)  б)
б) 
Решение. а) Подведем функцию 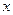 под знак дифференциала. Имеем:
под знак дифференциала. Имеем:

б) Подведем функцию  под знак дифференциала. Имеем:
под знак дифференциала. Имеем:

Итак, цель метода подведения под знак дифференциала состоит в видоизменении дифференциала, стоящего под интегралом, за счет использования свойств дифференциала.
2. Метод подстановки или метод замены переменной. Суть этого метода заключается в том, путем введения новой переменной интегрирования удается вести данный интеграл к новому интегралу, который сравнительной легко вычисляется непосредственно. Метод замены переменной основан на следующей теореме.
Теорема 8.3. Пусть функция  определена и дифференцируема на промежутке
определена и дифференцируема на промежутке  . Тогда если
. Тогда если  первообразная для
первообразная для 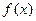 на
на 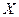 , то выполняется равенство
, то выполняется равенство 
Даная теорема называется формулой замены переменной в неопределенном интеграле.
Замечание 1. В практике интегрирования применяются подстановки вида  , т.е. новая переменная интегрирования вводится как некоторая функция переменной х.
, т.е. новая переменная интегрирования вводится как некоторая функция переменной х.
Замечание 2. При нахождении интеграла методом замены переменной необходимо в полученном после интегрирования результате обязательно вернуться к старой переменной.
Пример 8.3. Найти интеграл 
Решение. Введем новую переменную 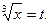 Такая замена обусловлена попыткой избавиться от корня в знаменателе подынтегрального выражения.
Такая замена обусловлена попыткой избавиться от корня в знаменателе подынтегрального выражения.
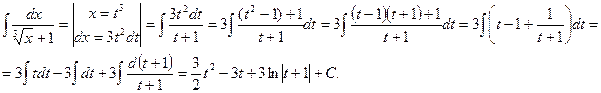 Теперь необходимо перейти к старой переменной x. Для этого в последнее выражение подставим
Теперь необходимо перейти к старой переменной x. Для этого в последнее выражение подставим  окончательно имеем
окончательно имеем
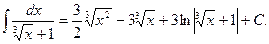
Удачная замена переменной позволяет упростить исходный интеграл и свести его к табличному.Полезно запомнить следующие подстановки:
|
|
|


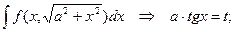

Число замен, которые могут быть применены при вычислении неопределенных интегралов велико и, конечно, обо всех рассказать не представляется возможным.
Метод интегрирования по частям
Пусть функции  и
и 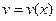 имеют непрерывные производные на промежутке
имеют непрерывные производные на промежутке 
Найдем дифференциал произведения этих функций:
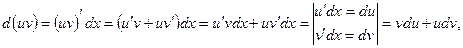
Поэтому, получим 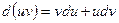 или
или 
Проинтегрируем обе части последнего равенства, получим
 ,
,
по свойству неопределенного интеграла?номер
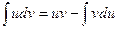
Эта формула называется формулой интегрирования по частям и составляет основу метода интегрирования по частям. Суть данного метода состоит в том в том, что при нахождении интеграла подынтегральное выражение  представляют в виде произведения множителей
представляют в виде произведения множителей 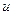 и
и  , при этом
, при этом  обязательно входит в
обязательно входит в  . Затем находят интегралы
. Затем находят интегралы 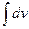 и
и 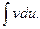 Естественно, что этот метод применим лишь в случае, если задача нахождения указанных интегралов более проста, чем задача нахождения заданного интеграла.
Естественно, что этот метод применим лишь в случае, если задача нахождения указанных интегралов более проста, чем задача нахождения заданного интеграла.
Пример 8.5. Найти интеграл 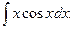
Решение. Применим к данному интегралу формулу интегрирования по частям, для этого за u обозначим x, а все остальное за  . Получим
. Получим

Заметим, что при нахождении v достаточно найти какую-нибудь одну из первообразных. Удобно считать C= 0.
Замечание.. Интегрирование по частям можно применять последовательно несколько раз в одном и том же примере.
Замечание. При вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители 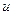 и
и  .
.
Замечание. Существуют целые классы интегралов, которые вычисляются с помощью формулы интегрирования по частям. Приведем ряд интегралов, которые находятся этим методом.
Рассмотрим интеграл вида 
1. Пусть  многочлен степени n, а
многочлен степени n, а 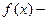 одна из следующих функций:
одна из следующих функций: 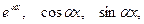 т.е.
т.е.

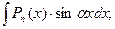
 (
(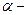 число).
число).
Рекомендуют положить  и применить метод n раз.
и применить метод n раз.
Пример 8.6. Вычислить 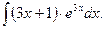
Решение. 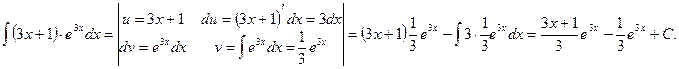 Пусть
Пусть  многочлен степени n, а
многочлен степени n, а 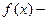 одна из следующих функций:
одна из следующих функций:  т.е.
т.е.
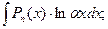
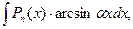


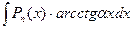 .
.
Рекомендуют положить 
Пример 8.7. Вычислить 
Решение.
 3. Пусть
3. Пусть 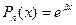 , а
, а 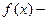 одна из следующих функций:
одна из следующих функций: 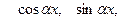 т.е.
т.е. 
 .
.
Возможно любое разбиение, при этом формула интегрирования по частям будет применяться дважды. Затем получим уравнение, в котором в качестве неизвестного выступает вычисляемый интеграл.
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3156; Нарушение авторских прав?; Мы поможем в написании вашей работы!