
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородного стержня
Частоты собственных продольных колебаний и удар
Система (13.1) после дифференцирования по z второго уравнения и подстановки первого уравнения дает
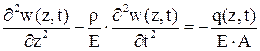 .
.
Уравнение линейно и его решение - сумма общего решения однородного уравнения и частного решения уравнения с правой частью. Здесь основным является решение однородного уравнения. Ограничимся им.
Представим решение в виде 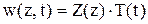 и подставим в однородное уравнение. Получаем
и подставим в однородное уравнение. Получаем
 ,
,
и, после преобразования (разделения переменных),
 ,
,
поскольку функции разных независимых переменных могут быть равны только в случае их равенства константе. Эта константа обозначена  и выбрана отрицательной, так как решение должно удовлетворять граничным условиям. Пояснения (**) ниже. Также введено обозначение
и выбрана отрицательной, так как решение должно удовлетворять граничным условиям. Пояснения (**) ниже. Также введено обозначение 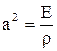 . Как известно из физики а - скорость распространения упругих волн в стержне. В этом нетрудно убедиться, так как
. Как известно из физики а - скорость распространения упругих волн в стержне. В этом нетрудно убедиться, так как 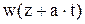 удовлетворяет однородному уравнению.
удовлетворяет однородному уравнению.
Система распадается на два обыкновенных дифференциальных уравнения


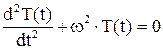 и
и  , решение которых
, решение которых 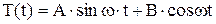 ,
,  ,
,
 должно удовлетворять граничным и начальным условиям задачи. Например, после удара стержня о стенку граничные условия:
должно удовлетворять граничным и начальным условиям задачи. Например, после удара стержня о стенку граничные условия: 
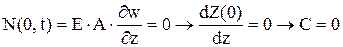 ,
,
 ,
,
откуда из основного свойства линейных уравнений – сумма решений есть решение-
 .
.
Частоты собственных колебаний определены:
 .
.
** При выборе положительной константы удовлетворить условиям на правом конце не удается.
Для определения амплитуд Аn, Bn необходимо удовлетворить начальным условиям:
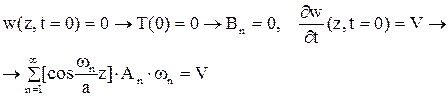
Для определения 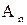 применим прием, приведший к разработке рядов Фурье. Умножим обе части последнего выражения на
применим прием, приведший к разработке рядов Фурье. Умножим обе части последнего выражения на  и проинтегрируем по длине стержня
и проинтегрируем по длине стержня
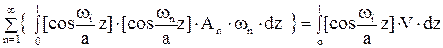 . (*)
. (*)
Сумма интегралов в левой части (*) равна 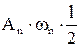 , т.к. после элементарных преобразований (***) легко убедится, что при
, т.к. после элементарных преобразований (***) легко убедится, что при

 , а при
, а при 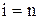
 .
.
Интеграл в правой части (*) равен  .
.
*** 
Только при 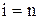 , раскрывая неопределенность типа 0/0, получаем
, раскрывая неопределенность типа 0/0, получаем  , в остальных случаях синус аргумента, пропорционального
, в остальных случаях синус аргумента, пропорционального 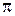 , равен нулю.
, равен нулю.
Окончательно из (*) получаем
 .
.
Соответственно
 ,
,
напряжения
 .
.
Максимальные напряжения при ударе о жесткую стенку упругого стержня, летящего со скоростью V, получим при 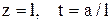 , т.е.
, т.е.
 .
.
Это точное решение. Для сравнения в одномассовой системе получаем
при массе, сосредоточенной в центре стержня,  ,
,
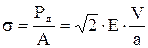 и расчет по одномассовой схеме дает запас
и расчет по одномассовой схеме дает запас  .
.
В качестве спецзадания предлагается провести расчет по двухмассовой схеме. Здесь запас будет меньше, но будет.
Частота собственных колебаний в одномассовой постановке
 ,
,
т.е. меньше точного решения. Подтверждается закономерность, подмеченная при сравнении одномассовой и двухмассовой моделей.
Вообще, расчет удара по конечномассовой схеме всегда дает запас, но тем меньше, чем выше порядок системы, а частоты приближаются к точным по мере повышения числа степеней свободы.
|
Дата добавления: 2014-01-20; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!