Всякая подгруппа является группой относительно операций исходной группы

Пример 6. Перечислим все подгруппы группы

s₃=<{P_i}, {*,^-1}> рассмотренной в примере 5.

1. Р₀s⁽⁰⁾ = <{P₀},{*,^-1} - тривиальная подгруппа, так как Р₀Р₀= Р₀, Р₀^-1= Р₀.

Заметим, что единичный элемент образует подгруппу в любой группе.

2.s₃⁽¹⁾= <{Р₀, P₁}, {*,^-1}>. Действительно:

Р₀Р₀= Р₀; Р₀Р₁= Р₁; Р₁Р₀= Р₁;

Р₁Р₁= Р₀; Р₀^-1= Р₀; Р₁^-1= Р₁;

Множество {Р₀,P₁} замкнуто относительно операции ком­позиции подстановок, содержит единичный элемент и обратный для любого своего элемента.

3. s₃⁽²⁾ = <{Р₀, P₂},{*,^-1} >.

4. s₃⁽³⁾ = <{Р₀, P₅},{*,^-1} >.

5. s₃⁽⁴⁾ = <{Р₀,Р₃,Р₄}, {*,^-1}>.

Сама группа s₃ является другим примером (наряду с s₃⁽⁰⁾) тривиальной подгруппы.

На множестве подгрупп группы s₃ можно ввести частичный порядок по отношению включения основных множеств. Диаграмма Хассе частично упорядоченного множества подгрупп s₃ группы подставок s₃ изображена на рис. 1.

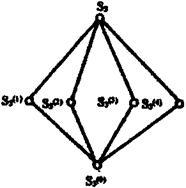
Рис.1.

Для группы справедлива теорема, аналогичная теореме 1 (лекция 2/2).

Теорема 4. Пересечение любого множества подгрупп является подгруппой.

Доказательство. Замкнутость пересечения относительно групповой операции следует из теоремы 1 (лекция 2/2). Поскольку единичный элемент содержится в любой подгруппе, то он со­держится и в их пересечении. Если а принадлежит пересечению подгрупп, то он принадлежит каждой подгруппе. Значит, каждой подгруппе принадлежит а^-1. Отсюда следует, что пересечение подгрупп вместе с любым своим элементом содержит и обратный ему элемент.

Пусть Н - подгруппа группы G и aÎG. Сформируем множест­во всех произведений вида ah, hÎH. Полученное множество на­зывается левым смежным классом по подгруппе H, определенным элементом а. Обозначается этот смежный класс символом аН. Аналогично определяется и правый смежный класс На.

Можно убедиться в том, что если аÎН, то аН=Н. Действи­тельно, с одной стороны. аНÍН, поскольку Н - подгруппа, а значит, она замкнута относительно групповой операции. С дру­гой стороны, если hÎН, то a^-1hÎH, h=а(а^-1h)ÎаН и ввиду произвольности hÎН имеем НÍаН. Значит, аН=Н. Аналогичный факт имеет место и для правых, смежных классов по подгруппе Н, определенных некоторыми элементами а.

Теорема 5. Множество левых (правых) смежных классов группы G по подгруппе Н образует разбиение группы G.

Доказательство. Для доказательства теоремы достаточно показать, что смежные классы не имеют общих, элементов и их объединение совпадает с G. Если aÎG, то а=ае, а так как еÎН, то аÎаН. Ввиду произвольности а любой элемент аÎН принадлежит некоторому смежному классу, так что их объедине­ние совпадает с G. Пусть существует хотя бы один элемент х, который принадлежит не менее чем двум смежным классам, т. е. хÎahÇbH, a,b,xÎG. Тогда х=аh₁=bh₂, где h₁ h₂ÎH. Значит. a=(bh₂)h₁^-1.

Возьмем произвольно qÎaH, тогда q=ah, hÎH, отсюда следует

q=ah=(bh₂)h₁^-1h=b(h₂ h₁^-1h).

Ввиду того, что h,h₁,h₂ÎH, справедливо h₂ h₁^-1ÎH. Послед­нее означает, что q входит в левый смежный класс подгруппы Н. Ввиду произвольности qÎaH можно сделать заключение аНÍbН. Аналогично доказывается обратное включение bНÍаН. Значит, аН=bН.

Таким образом, если два смежных класса группы G по подгруппе Н имеют хотя бы один общий элемент, то они совпа­дают. Поскольку по условию теоремы рассматриваются различные смежные классы, то они не пересекаются.

С помощью аналогичных рассуждений доказывается справед­ливость теоремы и для правых смежных классов.

Указанные в теореме 5 разбиения группы G называ­ются соответственно левым или правым разбиением группы G no подгруппе Н.

Определение 6. Число элементов группы G называ­ется ее порядком.

При изучении структуры (строения) группы большое значе­ние имеет нижеследующая теорема.

Теорема 6. Если n - порядок группы, m- порядок ее подгруппы, k - число правых смежных классов группы G по подгруппе Н, то n=km.

Доказательство. Пусть h₁,h₂,...h_mÎН - элементы подг­руппы Н. В смежный класс Н_a входят элементы h₁a,h₂a,...,h_ma. Все эти элементы различны, так как если h_ia=h_ja для некото­рых i и j, i,jÎ1(1)m, то

H_i=(h_ia)a^-1=(h_ia)a^-1=h_j,

т.е. h_i=h_j. Тогда каждый смежный класс по подгруппе Н содер­жит ровно m элементов и по теореме n=mk.

Следствие (теорема Лагранжа). Порядок подгруппы делит порядок группы (нацело).

Пример 7. Продемонстрируем основные понятия, введенные выше, на примере группы s₃ (см. ранее примеры 5 и 6).

Построим множество правых и левых смежных классов груп­пы s₃ no подгруппе s₃⁽³⁾, используя таблицу 2.

Левые смежные классы:

h₁=P₀; h₂=P₅⁰; s₃=<{h₁, h₂},{*,^-1}.;

P₀h₁ =P₀; P₀h₂ =P₅; B₀={P₀, P₅};

P₁h₁ =P₁; P₁h₂ =P₄; B₁={P₁, P₄};

P₂h₁ =P₂; P₂h₂ =P₃; B₂={P₂, P₃};

P₃h₁ =P₃; P₃h₂ =P₂; B₃ = B₂;

P₄h₁ =P₄; P₄h₂ =P₁; B₄ = B₁;

P₅h₁ =P₅; P₅h₂ =P₀; B₅ = B₀;

Итак, множество левых смежных классов группы s₃ по подгруппе s₃⁽³⁾ таково:

B₀={P₀, P₅}, B₁={P₁, P₄}, B₂={P₂, P₃}.

Очевидно, что смежные классы B₀, B_1, B₂ образуют разби­ение группы s₃.

Правые смежные классы:

h₁P₀ =P₀; h₂P₀ =P₅; A₀={P₀, P₅};

h₁P₁ =P₁; h₂P₁ =P₄; A₁={P₁, P₃};

h₁P₂ =P₂; h₂P₂ =P₃; A₂={P₂, P₄};

h₁P₃ =P₃; h₂P₃ =P₂; A₃ = A₁;

h₁P₄ =P₄; h₂P₄ =P₁; A₄ = A₂;

h₁P₅ =P₅; h₂P₅ =P₀; A₅ = A₀;

Множество правых смежных классов группы s₃ по подгруппе s₃⁽³⁾ таково:

A₀={P₀, P₅}, A₁={P₁, P₃}, A₂={P₂, P₄}.

Эти классы также образуют разбиение группы s₃⁽³⁾. Можно ви­деть, что правый и левый смежные классы по подгруппе s₃⁽³⁾ для элементов из s₃⁽³⁾ совпадают с основным множеством этой подгруппы.

Группа s₃ имеет порядок G, порядок подгруппы s_s⁽³⁾ равен трём. Как и следовало ожидать (см. теорему 6 и следствие из нее), число смежных классов равно трем.

Пример 8. Рассмотрим множество N целых чисел c операцией сложения, G=<N,{+,-}>. Роль единичного элемента в N относительно сложения играет нуль, для любого элемента nÎN обратным элементом является число -n. Таким образом, G=<N,{+,-}> является группой целых чисел по сложению, причем коммутативной (абелевой).

Пусть m - некоторое целое число, N_m={0±km, k=1,2,....} - подмножество множества целых чисел, которые нацело делятся на число m. Очевидно. G_m=<N_m,{+,-}> будет подгруппой гpyппы G=<N,{+,-}>.

Построим множество левых смежных классов группы G по подгруппе G_m для целых чисел 1,2,…,m-1. Ввиду коммутативности сложения левый смежный класс произвольного элемента совпадает с его правым смежным классом:

- для i=1

A₁={1, m+1, -m+1, 2m+1, -2m+1,...... };

- для i=2

A₂={2, m+2, -m+2, 2m+2, -2m+2,...... };

-------------------------------------------------

- для i=m-l

A_m-1={m-1, 2m-1-2, ……..};

- для i=m

A_m=N_m

Очевидно, что если брать числа i>m или i<0, то новых смежных классов не будет, поэтому A₁, А₂,…,A_m-1, Am_» образуют разбиения множества N группы G на смежные классы по подгруппе G_M. Поскольку m можно брать произвольным, то каждому из них можно поставить в соответствие множество смежных классов по соответствующей подгруппе, причем получающиеся при этом разбиения множества N получаются различными.

Полугруппы (дополнение)

Полугруппа – алгебра с одной ассоциативной

бинарной операцией

операция «умножения», для элементов

а и в записывается ав.

В общем слущае ав¹ва.

Если ав=ва (т.е. умножение коммутативно),

то полугруппа называется

коммутативной, или абелевой.

Дата добавления: 2014-01-11