Method of slowly changing amplitudes. Method preconditions. The truncated equations. Stationary conditions

Lecture 8

The lecture purpose is acquaintance with preconditions of a method of slowly changing amplitudes, formulation of the truncated equations and definition stationary аплитуд.

In practice real oscillatory systems always диссипативны also are to a greater or lesser extent nonlinear. Studying oscillations in poorly nonlinear systems with small attenuation at affecting on them of a harmonious superposed force, we study the oscillations close to harmonious, but not strictly harmonious. In the nature does not exist conservative and in strict sense of linear systems, hence, does not exist in practice of harmonic oscillations. For research of poorly nonlinear systems and it is weak диссипативных systems oscillations in which poorly differ from harmonious, it is developed and it is widely used strict асимптотический a method of theoretical research - a method of slowly changing amplitudes (ММА).

This method has been offered Van дер by the Field for research almost harmonic oscillations in poorly nonlinear systems and for the first time by it is applied to the equation solution:

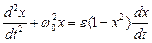, (1)

which presents oscillations in the oscillator with an LC tank in a circuit of a grid of the vacuum tube and with the feedback coil in an anode circuit. In this equation

x (t) =u (τ) cos (τ) +v (τ) sin (τ) – capacitance voltage. Nonlinearity of the anode-grid characteristic of an electronic tube was approximated by binomial of the third level.

Mean also 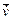we gain, computing definite integral within ­ one period τ = 2 π and dividing them for oscillations. We receive

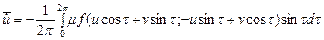, (2)

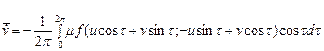. (3)

We gained two differential equations for amplitudes u(τ) and v(τ).

These are the non-linear equations, but they are easier than initial equations. The received equations are called as the truncated equations.

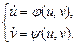(4)

These equations allow to find all stationary conditions of oscillatory system.

Lecture 9

Research of stability of stationary conditions

The lecture purpose is acquaintance with methods of research of stationary conditions on stability.

In stationary conditions of an amplitude of oscillation do not change eventually, that is and. The truncated equations for stationary regimes look like

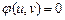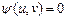, . (1)

Solving this system rather u and v, we find a steady-state value of amplitudes u_i and v_i. We give to stationary amplitudes u_i and v_i perturbations andx?andh? we observe the equations

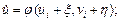
. (2)

Let's out functions and 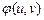in 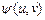sedate rows in the vicinity of a point.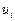

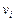
(3)

Oбозначим

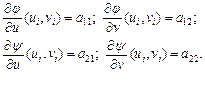(4)

On a stationarity condition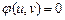;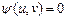. As a result we gain system of the linear differential first-order equations presenting small oscillations in a neighbourhood of a steady state.

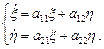
(5)

This system has the aspect solution:

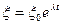, , (6)

Where and 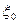- 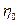initial perturbations. This system has nonzero solutions for ξ and η, if the determinant is equal to zero

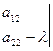=0, (7)

or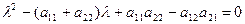. Roots of this quadratic eduation

, (8)

generally are complex quantities. If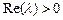, the steady state is not resistant to (deviations and x are eventually increase). If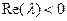, a system steady state resistantly to (deviations of x and h fade eventually).

Дата добавления: 2014-01-11