
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Т1. Если функция определена и интегрируема на сегменте , разлагается в тригонометрический ряд
|
|
|
|
 ,
,
который равномерно сходится, то это разложение единственно.
Док-во. Интегрируя почленно тригонометрический ряд (это можно делать в силу его равномерной сходимости (см. Лекцию № 21)), получим
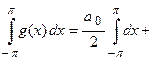
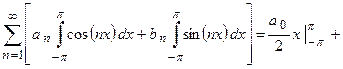
 .
.
Откуда находим, что  . Рассмотрим интегралы вида:
. Рассмотрим интегралы вида:
а)  ; б)
; б) 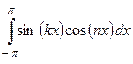 ; в)
; в)  .
.
В случае  :
:
а) 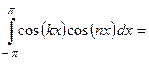 (как интеграл от четной функции по симметричному интервалу интегрирования (см. Лекцию № 8))
(как интеграл от четной функции по симметричному интервалу интегрирования (см. Лекцию № 8)) 

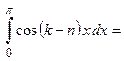
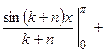
 .
.
б)  (как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8). Этот интеграл равен нулю и в случае
(как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8). Этот интеграл равен нулю и в случае  по той же причине).
по той же причине).
в)  (как интеграл от четной функции по симметричному ин-тервалу интегрирования (см. Лекцию № 8))
(как интеграл от четной функции по симметричному ин-тервалу интегрирования (см. Лекцию № 8)) 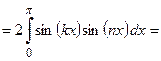
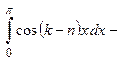
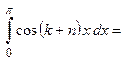

 .
.
В случае  :
:
а)  (как интеграл от четной функции по симметричному интервалу интегрирования)
(как интеграл от четной функции по симметричному интервалу интегрирования) 
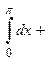


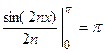 .
.
в) 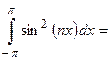 (как интеграл от четной функции по симметричному интервалу интегрирования)
(как интеграл от четной функции по симметричному интервалу интегрирования) 
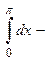


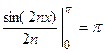 .
.
Умножим тригонометрический ряд на 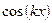 и проинтегрируем его на отрезке
и проинтегрируем его на отрезке  , получим:
, получим:

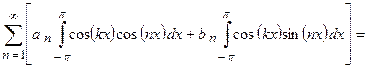 (с учетом полученных результатов)
(с учетом полученных результатов)  . Отсюда находим, что
. Отсюда находим, что 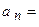
 .
.
Умножим тригонометрический ряд на  и проинтегрируем его на отрезке
и проинтегрируем его на отрезке  , получим:
, получим:

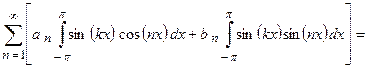
(с учетом полученных результатов) . Отсюда находим, что
. Отсюда находим, что 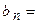
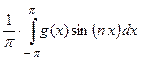 .
.
Итак, коэффициенты тригонометрического ряда однозначно определяются формулами:  ;
; 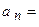
 ;
; 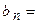
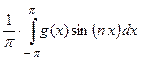 . Следовательно, разложение функции в тригонометрический ряд единственно.
. Следовательно, разложение функции в тригонометрический ряд единственно.
О3. Тригонометрический ряд с коэффициентами, определяемыми формулами:  ;
; 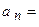
 ;
; 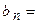
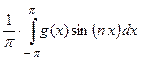 называется рядом Фурье.
называется рядом Фурье.
Пример 1. Разложить в ряд Фурье функцию  на сегменте
на сегменте  .
.
Для того чтобы разложить в ряд Фурье функцию  на сегменте
на сегменте  , необходимо и достаточно вычислить коэффициенты этого ряда:
, необходимо и достаточно вычислить коэффициенты этого ряда: 
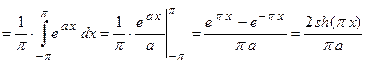 ;
;
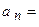
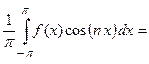
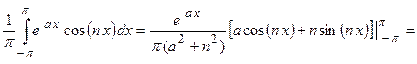
 ;
;
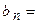
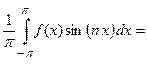

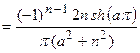 .
.
Следовательно, разложение в ряд Фурье функции 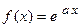 имеет вид:
имеет вид:

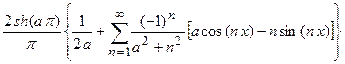 .
.
З1. Если функция 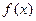 периодична с периодом
периодична с периодом  и разлагается в
и разлагается в
ряд Фурье, то ее можно разложить на любом интервале длиной 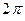 , например,
, например,  ,
, 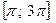 или
или  .
.
|
|
|
Пример 2. Разложить в ряд Фурье функцию  на сегменте
на сегменте  .
.
Вычислим коэффициенты ряда Фурье

 ;
;
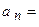
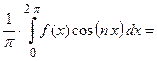
 ;
;
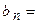

 .
.
Таким образом,  .
.
Лекция № 24 “Ряд Фурье для четных и нечетных функций”
1. Сходимость ряда Фурье.
О4. Функция  , определенная на всей числовой оси и периодическая с периодом
, определенная на всей числовой оси и периодическая с периодом  , называется периодическим продолжением функции
, называется периодическим продолжением функции 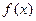 , если на сегменте
, если на сегменте 
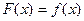 .
.
Очевидно, что если на сегменте  ряд Фурье сходится к функции
ряд Фурье сходится к функции 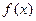 , то он сходится на всей числовой оси к функции
, то он сходится на всей числовой оси к функции  . В связи с этим в заключение лекции рассмотрим теорему о сумме ряда Фурье на всей числовой оси.
. В связи с этим в заключение лекции рассмотрим теорему о сумме ряда Фурье на всей числовой оси.
Т2. Пусть функция 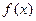 и ее производная
и ее производная  непрерывны на сегменте
непрерывны на сегменте  или имеют на этом интервале конечное число точек разрыва первого рода. Тогда ряд Фурье функции
или имеют на этом интервале конечное число точек разрыва первого рода. Тогда ряд Фурье функции 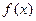 сходится на сегменте
сходится на сегменте  , причем в каждой точке
, причем в каждой точке 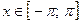 , в которой функция
, в которой функция 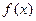 непрерывна сумма ряда равна
непрерывна сумма ряда равна 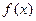 ; в каждой точке разрыва первого рода
; в каждой точке разрыва первого рода  функции
функции 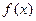 сумма ряда будет равна
сумма ряда будет равна 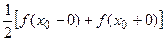 , где
, где
 и
и  ;
;
на концах сегмента  сумма ряда будет равна
сумма ряда будет равна  . Если функция
. Если функция  является периодическим продолжением функции
является периодическим продолжением функции 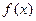 , то аналогичные утверждения имеют место и для функции
, то аналогичные утверждения имеют место и для функции  на всей чис-ловой оси.
на всей чис-ловой оси.
Пример 1. Разложить в ряд Фурье периодическое продолжение функции 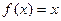 на сегменте
на сегменте 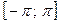 .
.
Так как 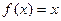 , то ее периодическое продолжение
, то ее периодическое продолжение  имеет вид (Рис. 24):
имеет вид (Рис. 24):
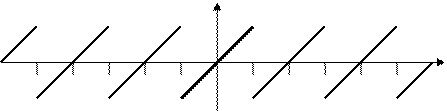
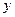
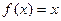




Рис. 24. Периодическое продолжение  функции
функции 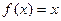 на
на 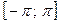 .
.

 (как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8)).
(как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8)).
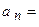

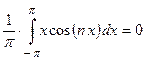 (как интеграл от нечетной функции по симметричному интервалу интегрирования).
(как интеграл от нечетной функции по симметричному интервалу интегрирования).
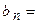
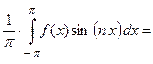
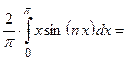 (как интеграл от четной функции по симметричному интервалу интегрирования)
(как интеграл от четной функции по симметричному интервалу интегрирования)  . Таким образом, ряд Фурье имеет вид
. Таким образом, ряд Фурье имеет вид 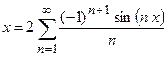 .
.
2. Ряд Фурье для четных и нечетных функций.
Пусть функция 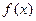 определена на сегменте
определена на сегменте  и является четной функцией, т.е.
и является четной функцией, т.е.  , тогда в ее ряде Фурье все коэффициенты
, тогда в ее ряде Фурье все коэффициенты  . Действительно
. Действительно 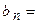
 (как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8)). С учетом четности функции
(как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8)). С учетом четности функции 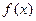 остальные коэффициенты вычисляются по формулам
остальные коэффициенты вычисляются по формулам
|
|
|
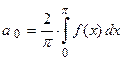 и
и 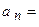
 ,
,
где был использован факт, что определенный интеграл от четной функции по симметричному интервалу интегрирования равен
 . Для не-четной на сегменте
. Для не-четной на сегменте 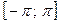 функции (
функции (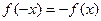 ) коэффициенты ряда Фурье определяются формулами
) коэффициенты ряда Фурье определяются формулами 
 и
и 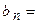
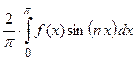 .
.
З1. Если функция 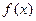 четна, то в ее ряде Фурье содержатся только
четна, то в ее ряде Фурье содержатся только
косинусы; в этом случае говорят, что функция разложена в ряд Фурье по косинусам или четным образом. Если функция 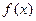 нечетна, то в ее ряде Фурье содержатся только синусы; в этом случае говорят, что функция разложена в ряд Фурье по синусам или нечетным образом.
нечетна, то в ее ряде Фурье содержатся только синусы; в этом случае говорят, что функция разложена в ряд Фурье по синусам или нечетным образом.
Пример 2. Разложить в ряд Фурье функцию 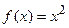 на сегменте
на сегменте 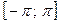 .
.
Так как функция 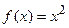 , то в ее ряде Фурье все коэффициенты
, то в ее ряде Фурье все коэффициенты  . Найдем оставшиеся коэффициенты ряда Фурье:
. Найдем оставшиеся коэффициенты ряда Фурье:
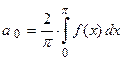
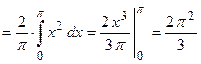 ;
;
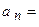


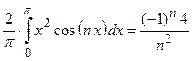 (вычислить самостоятельно).
(вычислить самостоятельно).
Итак, ряд Фурье имеет вид: 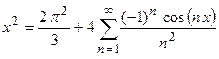 .
.
3. Ряд Фурье для функций с периодом  и
и  .
.
Пусть функция 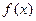 определена на сегменте
определена на сегменте  и удовлетворяет всем требованиям теоремы Фурье, тогда ее можно разложить в ряд Фурье. Если ввести новую переменную
и удовлетворяет всем требованиям теоремы Фурье, тогда ее можно разложить в ряд Фурье. Если ввести новую переменную  и рассмотреть функцию
и рассмотреть функцию 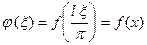 . Очевидно, что функция
. Очевидно, что функция 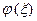 определена на сегменте
определена на сегменте 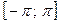 и ее разложение в ряд Фурье имеет вид:
и ее разложение в ряд Фурье имеет вид: 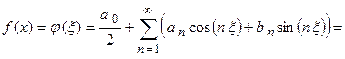
 ,
,
где коэффициенты ряда определяются формулами
 ;
; 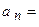
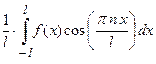 ;
; 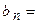
 .
.
Если функция 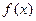 определена на произвольном сегменте
определена на произвольном сегменте  , периодична с периодом
, периодична с периодом 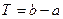 и удовлетворяет условиям теоремы Фурье, то ее можно разложить в ряд Фурье, который имеет вид:
и удовлетворяет условиям теоремы Фурье, то ее можно разложить в ряд Фурье, который имеет вид:
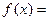
 ,
,
где коэффициенты ряда определяются формулами
 ;
; 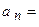
 ;
; 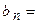
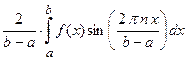 .
.
В заключение отметим, что ряд Фурье является частным случаем функционального ряда, который равномерно сходится к своей сумме. Следовательно, его можно почленно дифференцировать и интегрировать.
Пример 3. Разложить в ряд Фурье функцию  на сегменте
на сегменте 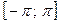 .
.
Воспользуемся разложением в ряд Фурье функции 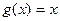 . Так как производная
. Так как производная 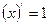 , то продифференцируем ряд Фурье для функции
, то продифференцируем ряд Фурье для функции 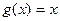 (см. Пример 1 этой Лекции)
(см. Пример 1 этой Лекции) 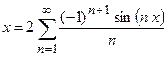
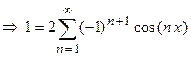 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 331; Нарушение авторских прав?; Мы поможем в написании вашей работы!