
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проблема заполнения разреженной матрицы системы при исключениях
|
|
|
|
Пусть рассматривается задача о решении неоднородной СЛАУ
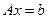 ,
,
где  матрица системы
матрица системы  является разреженной симметричной и положительно определенной. В силу симметричности и положительной определенности
является разреженной симметричной и положительно определенной. В силу симметричности и положительной определенности  рассматривую систему имеет смысл решать методом Холесского (см.лекцию 7). Для простоты изложения рассмотрим простой пример.
рассматривую систему имеет смысл решать методом Холесского (см.лекцию 7). Для простоты изложения рассмотрим простой пример.
Пусть требуется решить СЛАУ
 .
.
Матрица системы  разреженная, симметричная, положительно определенная. Построим для нее симметричное разложение:
разреженная, симметричная, положительно определенная. Построим для нее симметричное разложение:

 .
.
При проведении симметричного разложения, мы получим:
 .
.
Решая систему  , получаем
, получаем  . Затем, решая систему
. Затем, решая систему  находим
находим 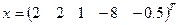 .
.
Этот пример иллюстрирует очень важный факт, относящийся к применению метода Холесского для системы с разреженной матрицей  : матрица обычно претерпевает заполнение. Это означает, что
: матрица обычно претерпевает заполнение. Это означает, что 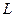 имеет ненулевые элементы в позициях, где в нижней треугольной части
имеет ненулевые элементы в позициях, где в нижней треугольной части  стояли нули. Это приводит к тому, что при хранении разреженной матрицы
стояли нули. Это приводит к тому, что при хранении разреженной матрицы  ее нули также прийдется хранить, т.к. в процессе исключения эти нули станут ненулевыми элементами и внесут свой вклад при решении СЛАУ.
ее нули также прийдется хранить, т.к. в процессе исключения эти нули станут ненулевыми элементами и внесут свой вклад при решении СЛАУ.
Предположим теперь, что мы перенумеровали переменные в соответствии с правилом:  , и переупорядочили уравнения так, чтобы последнее стало первым, второе снизу - вторым сверху и т.д., пока, наконец, бывшее первое уравнение не станет последним. Мы получим СЛАУ, эквивалентную данной:
, и переупорядочили уравнения так, чтобы последнее стало первым, второе снизу - вторым сверху и т.д., пока, наконец, бывшее первое уравнение не станет последним. Мы получим СЛАУ, эквивалентную данной:
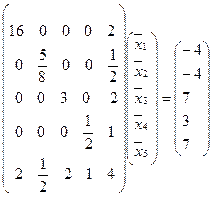 .
.
Проведенная перенумерация неизвестных и переупорядочение уравнений равносильны симметричной перестановке строк и столбцов матрицы  (симметричная перестановка строк и столбцов означает: если в матрице
(симметричная перестановка строк и столбцов означает: если в матрице  меняются местами
меняются местами 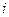 -ая и
-ая и  -ая строки, то меняются местами также
-ая строки, то меняются местами также 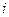 -ый и
-ый и  -ый столбец. В матричном виде симметричная перестановка будет означать умножение матрицы
-ый столбец. В матричном виде симметричная перестановка будет означать умножение матрицы  на соответствующую матрицу перестановки справа и слева), причем та же перестановка применяется и к
на соответствующую матрицу перестановки справа и слева), причем та же перестановка применяется и к 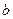 .Эту новую систему обозначим
.Эту новую систему обозначим 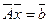 . Применяя к ней метод Холесского, разложим матрицу
. Применяя к ней метод Холесского, разложим матрицу  , где нижний треугольный множитель будет иметь вид:
, где нижний треугольный множитель будет иметь вид:
|
|
|
 .
.
Решая системы  и
и 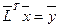 , получим решение
, получим решение  , которое есть лишь переупорядоченная форма
, которое есть лишь переупорядоченная форма  . Важнейший момент состоит в том, что переупорядочение уравнений и переменных привело к треугольному множителю
. Важнейший момент состоит в том, что переупорядочение уравнений и переменных привело к треугольному множителю  , который разрежен в точности в той мере, что и нижний треугольник
, который разрежен в точности в той мере, что и нижний треугольник  . В этом случае нулевые элементы
. В этом случае нулевые элементы  можно не хранить, т.к. они останутся нулями и после исключения и не внесут никакого вклада в решение треугольных систем, полученных после проведения разложения Холесского.
можно не хранить, т.к. они останутся нулями и после исключения и не внесут никакого вклада в решение треугольных систем, полученных после проведения разложения Холесского.
Хотя на практике редко удается достигнуть столь полного успеха, для большинства задач с разреженными матрицами разумное упорядочение строк и столбцов матрицы коэффициентов может дать огромное сокращение заполнения и, следовательно, экономию машинного времени и памяти (при условии, что разреженность используется).
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 339; Нарушение авторских прав?; Мы поможем в написании вашей работы!