Множества и отображения

N 3 4 5 6 7 8 9 10 20 30 60

a_n 0,204 0,250 0,256 0,250 0,243 0,231 0,222 0,212 0,156 0,128 0,091.

Вычислим значения коэффициента k_n и относительную ошибку площади для некоторых правильных многоугольников:

- для треугольника (n=3) k_n=4,24 и m_p/P = 4,24× m_t/L,

- для четырехугольника (n=4) k_n=4,00 и m_p/P = 4,00× m_t/L,

- для пятиугольника (n=5) k_n=3,72 и m_p/P = 3,72×m_t/L,

- для шестиугольника (n=6) k_n=3,46 и m_p/P = 3,46× m_t/L.

Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу

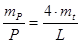;(9.6)

ошибка этой формулы может достигать 15% - 20% для участков, форма которых заметно отличается от формы правильного n -угольника. Вывод формулы (9.3) приведён в [13]; это - формула Маслова; формул (9.4) и (9.5) выведены Дьяковым Б.Н. в [14]; они предназначены для оперативной оценки точности площади. Естественно предположить, что результаты вычислений по разным формулам для одного и того же многоугольника должны совпадать, однако в действительности это условие часто не выполняется.

Для примера вычислим ошибку площади квадрата со стороной 200 м при заданной ошибке положения вершин квадрата m_P=0,10м; результаты для всех трёх формул получились совершенно одинаковые:

- по формуле (9.2), K=1, m_P=20 кв.м;

- по формуле (9.3), D₁=D₂=D₃=D₄=200м*1,414=282,8м, m_P=20 кв.м;

- по формуле (9.4), a₄=0,25, L=800м, m_P=20 кв.м.

Второй пример вычисления ошибки площади решим для прямоугольника с тем же периметром L=800м. В этом примере n=4, K=3,D₁=D₂=D₃=D4=D=316,2м, a₄=0,25, и значение ошибки получается:

- по формуле (9.2), m_P=22,4 кв.м;

- по формуле (9.3), m_P=22,4 кв.м;

- по формуле (9.4), m_P=20,0 кв.м.

Третий пример вычисления ошибки площади решим для правильного шестиугольника с тем же периметром L=800м. В этом примере n=6, K=1,D₁=D₂=D₃=D4=D=230,9м, a₆=0,25, и значение ошибки получается:

- по формуле (9.2), m_P=21,5 кв.м;

- по формуле (9.3), m_P=20,0 кв.м;

- по формуле (9.4), m_P=20,0 кв.м.

Продолжая вычисления ошибки площади для других многоугольников, мы обнаружили следующие закономерности:

- формула (9.2) пригодна для оценки точности площади только прямоугольных четырёхугольников;

- значения ошибки площади для правильных многоугольников, получается одинаковой как при вычислении её по формуле (9.3), так и по формуле (9.4);

- в остальных случаях результаты вычислений по формулам (9.3) и (9.4) будут различаться, и хотя это различие невелико (порядка единиц процентов) и заметно только для многоугольников с явно выраженным чередованием длинных и коротких сторон, в отдельных случаях с этим нужно считаться.

Строгая оценка точности площади как функции координат вершин многоугольника описана, например, в [15]; она базируется на частном дифференцировании известной формулы площади

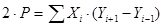, (7)

где P – площадь многоугольника; X, Y – прямоугольные координаты вершин.

Даже при независимом определении координат вершин многоугольника при оценке точности площади необходимо учитывать корреляцию ошибок координат X и Y одной вершины, так как ошибка положения одной точки характеризуется тройкой чисел m_X, m_Y, m_XY [15]; в общем случае следует учитывать и корреляцию ошибок координат разных вершин многоугольника. Чтобы получить более или менее удобную для практических вычислений формулу, приходится принимать дополнительные условия. Так, при выводе формулы (9.3) в [13] приняты условия, что ошибки координат одной вершины независимы (m_XY = 0) и равны между собой ( m_X = m_Y = m ). Этим условиям соответствует только определение координат по координатной сетке топографических карт и планов; при полевых определениях координат эти условия не соблюдаются в принципе, а потому применение формулы (9.3) в этом случае нельзя считать обоснованным.

Преобладающей формой земельных участков является прямоугольный четырёхугольник, поэтому будет уместным привести формулы для оценки точности площади прямоугольника. Обозначим, как и в [12] через l короткую сторону прямоугольника, а через Kl – длинную его сторону, где K – коэффициент вытянутости, и, используя формулы (9.2), (9.3) и (9.4) как исходные, получим (при условии, что ошибки положения всех вершин одинаковые) следующие формулы для прямоугольного четырёхугольника:

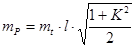, (9.8)

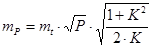, (9.9)

. (9.10)

Как уже отмечалось выше, все три формулы (9.8), (9.9), (9.10) дают совершенно одинаковые результаты, но, как и исходные формулы, они являются приближёнными. Для квадрата ( K=1 ) эти формулы ещё упрощаются и принимают вид

, (9.11)

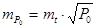, (9.12)

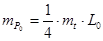. (9.13)

Представляет интерес применение упрощенных формул (9.12) и (9.13) для оценки точности площади произвольного прямоугольника (при K>1 ). Для этого построим графики функции m_P/m_P0 при P=Const и L=Const и изменяющемся значении коэффициента вытянутости K (рис.9.2). Предельное значение этой функции при L=Const равно 1,414; то есть ошибка формулы (9.13) не превысит 41% при любом значении K, а при K<6 – она будет меньше 20%. Формулы (9.11) и (9.12) таким свойством не обладают.

В заключение приведём общие выводы:

- строгую оценку точности площади многоугольника следует выполнять с учётом корреляционной матрицы координат его вершин;

- все конечные формулы для оценки точности площади многоугольника являются приближёнными; при независимом определении координат ошибки этих формул могут достигать 10% - 20%;

- наиболее рациональной формулой для практических вычислений является формула (9.4), однако для многоугольников сложной формы (типа неравносторонняя звезда) предпочтительнее формула (9.3);

- ошибку площади прямоугольника при K<6 следует выполнять по формулам (9.4) или (9.13), в остальных случаях – по формуле (9.3).

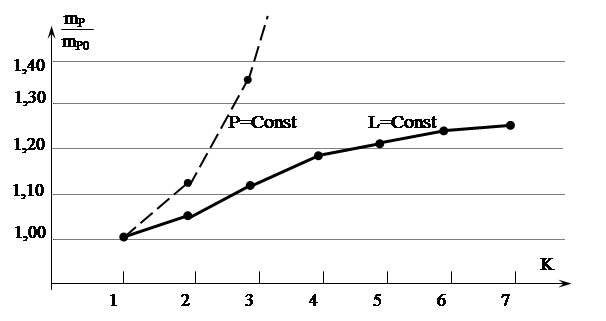Рис.9.2 – Графики функции m_P/m_P0

ЛИТЕРАТУРА

1. Селиханович В.Г. Геодезия. Ч.2. М.: Недра, 1981.

2. Селиханович В.Г., Козлов В.П., Логинова Г.П. Практикум по геодезии, М.: Недра, 1973.

3. Дьяков Б.Н. Геодезия. Общий курс. Новосибирск: СГГА, 1997 (электронная версия на сайте www.spmi-ig.narod.ru).

4. Закатов П.С. Высшая геодезия. М.: Недра, 1976.

5. Инструкция по нивелированию I, II, III, IY классов. М.: Недра, 1990.

6. Инструкция по полигонометрии и трилатерации. М.: Недра, 1976.

7. Инструкция по топографическим съёмкам масштабов 1:5000, 1:2000, 1:1000 и 1:500. М.: Недра, 1989.

8. Инструкция о построении государственной геодезической сети СССР. М.: Недра, 1966.

9. Инструкция о построении государственной геодезической сети РФ. М.: Картгеоцентр-Геодезиздат, 2001.

10. Единая государственная система геодезических координат 1995 года (СК-95). М.: ЦНИИГАиК, 2000.

11. Коськов Б.И. Справочное руководство по съёмке городов. 2-е изд., перераб. и доп. – М.: Недра, 1974.

12. Инструкция по межеванию земель. М.: Роскомзем, 1996.

13. Маслов А.В., Горохов Р.И., Ктиторов Э.М. и др. Геодезические работы при землеустройстве. – М.:

Недра, 1976. – 256 с.

14. Дьяков Б.Н. Оперативная оценка точности площади замкнутого контура с прямолинейными

границами//Геодезия и картография. – 1996. – N 2. – с.39.

15. Лапина А.В., Мицкевич В.И. Вычисление и предвычисление точности определения площади//Геодезия и картография. – 1993. – N 8. – с.50.

1.1 Операции над множествами

Пусть X – некоторое множество (совокупность); природа составляющих его объектов (элементов) значения не имеет. Если x является элементом множества X, записывают x Î X (следует читать: x принадлежит X), запись x Ï X означает, что x не является элементом X

Пусть X и Y – некоторые множества. Если каждый элемент множества X принадлежит и множеству Y, то X называют подмножеством множества Y, при этом записывают: X Ì Y.

Будем говорить, что множества X и Y равны и записывать при этом X = Y, если X и Y состоят из одних и тех же элементов, т.е. если каждый элемент X принадлежит Y (X Ì Y), а каждый элемент Y принадлежит X (Y Ì X).

Объединением множеств X и Y называют множество, состоящее из всех эле- ментов X и всех элементов Y; обозначают такое множество через .

Пересечением множеств X и Y называют совокупность элементов, принадле- жащих и множеству X, и множеству Y; обозначают такое множество через .

Разностью множеств X и Y называют множество тех элементов X, которые не принадлежат Y; обозначают такое множество через X \ Y.

X \ Y

Рис. 1.

На рис.1 заштрихованные фигуры изображают объединение, пересечение и раз- ность двух множеств X и Y, представленных прямоугольниками.

1.2. Отображения.

Пусть заданы множества X и Y, и пусть сформулировано правило f, согласно которому каждому элементу х Х сопоставлен некоторый элемент у Y. Правило f называют отображением множества Х в множество Y, элемент у называют образом

Рис.2.

элемента х при отображении f, а х называют прообразом у при отображении f (рис.2).

Мы будем пользоваться общепринятой символикой:

f: X ® Y – отображение f множества X в множество Y;

y = f (x) – y есть образ элемента x при отображении f;

f (X) – образ множества X при отображении f, т.е. множество тех элемен- тов из Y, которые являются образами элементов из X при отображении f.

Пусть задано отображение f: X ® Y. Говорят, что f отображает X на Y взаимно однозначно, если 1) Y = f (X), т.е. каждый элемент множества Y является образом хотя бы одного элемента множества X при отображении f, и 2) образы различных между собой элементов множества X различны, т.е. из следует .

Из 1) и 2) следует, что при взаимно однозначном отображении f множества X на Y для каждого элемента y Î Y в множестве X обязательно существует, и притом только один прообраз. Единственность прообраза для каждого элемента y Î Y позво- ляет рассматривать отображение множества Y в множество X, при котором каждому элементу y Î Y сопоставлен его прообраз х, x Î X, при отображении f. Такое ото- бражение множества Y в множество X называют обратным по отношению к отобра- жению f и обозначают символом . Заметим, что обратное отображение оп- ределено только для взаимно однозначного отображения f; отображение :Y® X взаимно однозначно отображает Y на X. Образ элемента x при отображении f яв- ляется прообразом элемента x при отображении , т.е. f есть отображение, обрат- ное по отношению к отображению ; f и -– это пара взаимно обратных ото- бражений.

Дата добавления: 2014-01-11