
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Следование, эквивалентность и преобразование формул
|
|
|
|
Задачи определения эквивалентности, выполнимости, опровержимости, тождественной истинности и ложности формул могут решаться с помощью построения таблиц истинности, однако существуют менее громоздкие способы решения этих задач.
Введем на множестве M логических формул отношения следования и эквивалентности.
Def. Формула B следует из формулы A (обозначается A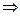 B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
Теорема 2.1. Формула B следует из формулы A тогда и только тогда, когда тождественно истинна формула A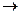 B.
B.
Доказательство. Пусть формула B следует из формулы A. Импликация A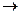 B ложна только на тех интерпретациях, на которых формула А истинна, а В ложна, что невозможно в силу условия теоремы.
B ложна только на тех интерпретациях, на которых формула А истинна, а В ложна, что невозможно в силу условия теоремы.
Покажем обратное. Пусть A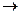 B – тождественно истинна. Тогда, если на некоторой интерпретации формула А истинна, то для истинности импликации надо, чтобы и формула В была истинна на этой интерпретации. Это и означает A
B – тождественно истинна. Тогда, если на некоторой интерпретации формула А истинна, то для истинности импликации надо, чтобы и формула В была истинна на этой интерпретации. Это и означает A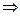 B.
B.
Def. Формула A эквивалентна формуле B (обозначается A º B), если они следуют друг из друга, то есть A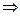 B и B
B и B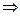 A. Легко показать, что это определение эквивалентно определению, введенному ранее в п.1.
A. Легко показать, что это определение эквивалентно определению, введенному ранее в п.1.
Теорема 2.2. Формула A эквивалентна формуле B тогда и только тогда, когда тождественно истинна формула A ~ B.
Доказательство аналогично доказательству теоремы 2.1.
Приведем список основных тавтологий, выражающих свойства логических операций.
1. Коммутативность:
X ÙY º Y ÙX, X ÚY º YÚX.
2. Ассоциативность:
(X ÙY)ÙZ º X Ù(YÙZ), (XÚY)ÚZ º XÚ(YÚZ).
3. Идемпотентность:
XÙX º X, XÚX º X.
4. Законы поглощения:
XÚ(X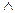 Y) º X, X
Y) º X, X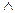 (XÚY) º X.
(XÚY) º X.
5. Взаимная дистрибутивность конъюнкции и дизъюнкции:
|
|
|
X Ù(YÚZ) º (X ÙY)Ú(X ÙZ), XÚ (YÙZ) º (XÚY)Ù(XÚZ).
6. Свойства констант:
XÙ0 º Л, XÙ1 º X,
XÚ0 º X, XÚ1 º 1.
7. Законы де Моргана:  ,
,  .
.
8. Инволютивность: 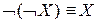 .
.
9. Закон противоречия:  º 0.
º 0.
10. Закон исключенного третьего:  º 1.
º 1.
Эквивалентность большинства из этих формул непосредственно следует из определения операций или проверяется построением таблиц истинности.
Пусть U – некоторая формула, в которую входит переменная X или подформула А, что обозначается U (¼, X,¼) или U (¼, А,¼). Пусть В – некоторая формула. Запись U (¼, X,¼){ В // X } обозначает формулу, полученную из формулы U подстановкой формулы В вместо всех вхождений переменной X, а U (¼, А,¼){ В / А } – формулу, полученную из формулы U подстановкой формулы В вместо некоторых (в частности, вместо одного) вхождений подформулы А.
В дальнейшем U (¼, X,¼){ В // X } будем называть операцией подстановки, а U (¼, X,¼){ В / X } – операцией замены.
Теорема 2.3 (правило подстановки). Если U (¼, X,¼) – тавтология и В – любая формула, то U (¼, X,¼){ В // X } – тавтология.
Теорема 2.4 (правило замены). Если A есть некоторая подформула формулы U и A эквивалентна формуле B, то формула, полученная заменой A в формуле U на B, эквивалентна U. Иными словами, если U (¼, А,¼) и A º B, то U º V = U (¼, А,¼){ В / А }.
Например, имеем формулу U = (X®Y)ÙZ. A = (X®Y) – подформула в U. В = 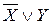 – подформула, эквивалентная А. Тогда (X®Y)ÙZ º (
– подформула, эквивалентная А. Тогда (X®Y)ÙZ º ( )ÙZ.
)ÙZ.
Следствие из 2.4. Если U~A и V~B, то:
1) U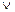 V º A
V º A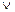 B;
B;
2) U V º A
V º A B;
B;
3) U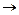 V º A
V º A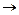 B;
B;
4) (U ~ V) º (A ~ B);
5) 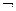 U º
U º 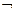 A.
A.
Теоремы 2.3, 2.4 и её следствие позволяют преобразовывать формулы, упрощая их, и доказывать эквивалентность формул.
|
|
|
Дата добавления: 2014-01-11; Просмотров: 534; Нарушение авторских прав?; Мы поможем в написании вашей работы!