
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выводимость
|
|
|
|
Пусть задано множество формул от высказывательных переменных 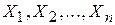
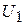 (
( ),
), 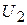 (
( ),...,
),..., 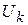 (
( ). (8.1)
). (8.1)
Это множество формул назовем системой посылок.
Определение. Формула  (
( ) называется выводимой из системы формул (1) в алгебре высказываний, что обозначается
) называется выводимой из системы формул (1) в алгебре высказываний, что обозначается  ,..,
,..,  ú-
ú-
 , тогда и только тогда, когда формула
, тогда и только тогда, когда формула
 (8.2)
(8.2)
является ТИ-высказыванием.
Из определения следует, что если конъюнкция
 (8.3)
(8.3)
тождественно истинна, то из такой системы посылок (8.1) выводимы только тождественно истинные формулы, которые выводимы из любой системы посылок. Если же конъюнкция (8.3) тождественно ложна, то из системы посылок (8.1) выводима любая формула.
Нетрудно доказать следующие свойства выводимости.
1. Если  ú-
ú-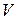 и
и 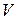 ú-
ú-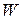 то
то  ú-
ú- 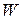 .
.
2. Если  ú-
ú-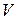 и
и 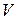 ~
~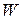 , то
, то  ú-
ú-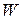 .
.
Проверка выводимости формулы  из системы посылок (1) непосредственно по определению, т.е. путем доказательства тождественной истинности формулы (2), достаточно громоздко. Рассмотрим более простой способ доказательства выводимости формулы
из системы посылок (1) непосредственно по определению, т.е. путем доказательства тождественной истинности формулы (2), достаточно громоздко. Рассмотрим более простой способ доказательства выводимости формулы  из системы посылок (1), для которых конъюнкция (3) не является ни ТИ-высказыванием, ни ТЛ-высказыванием.
из системы посылок (1), для которых конъюнкция (3) не является ни ТИ-высказыванием, ни ТЛ-высказыванием.
Теорема 8.1. Формула  (
( ) тогда и только тогда выводима из системы формул (8.1), когда все полные элементарные дизъюнкции формулы
) тогда и только тогда выводима из системы формул (8.1), когда все полные элементарные дизъюнкции формулы  входят в СКН-форму
входят в СКН-форму  , эквивалентную формуле (8.3) относительно высказывательных переменных
, эквивалентную формуле (8.3) относительно высказывательных переменных  .
.
Так как теорема 8.1 формулирует необходимое и достаточное условие выводимости формулы, то на основе нее можно сформулировать алгоритм доказательства выводимости формулы.
1. Из системы посылок (8.1) строится конъюнкция (8.3).
2. Находим СКН-форму от высказывательных переменных для формулы (8.3).
3. Строим СКН-форму для формулы  и проверяем вхождение полных элементарных дизъюнкций СКН-формы для формулы
и проверяем вхождение полных элементарных дизъюнкций СКН-формы для формулы  в СКН-форму для формулы (8.3).
в СКН-форму для формулы (8.3).
|
|
|
Задание 1. Доказать выводимость 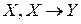 ú-
ú-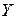 .
.
Решение.
1. Обозначим  = X,
= X, 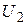 =
=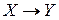 . Строим их конъюнкцию
. Строим их конъюнкцию  .
.
2. Найдем СКН-форму 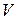 эквивалентную этой конъюнкции.
эквивалентную этой конъюнкции.
 V.
V.
3. Получим СКН-форму для формулы B  :
: 
Так как обе дизъюнкции входят в СКН-форму 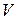 , то выводимость доказана.
, то выводимость доказана.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 694; Нарушение авторских прав?; Мы поможем в написании вашей работы!