
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные общезначимости алгебры предикатов
|
|
|
|
1. 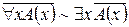

2. 
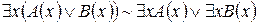
3. 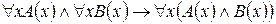
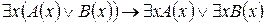
4. 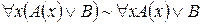
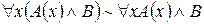
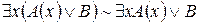

5. 

Докажем формулу  .
.
Так как единственная переменная в обеих частях эквиваленции связана, то обе они являются высказываниями. Поэтому для доказательства общезначимости формулы, покажем, что истинностные значения левой и правой части совпадают для любых одноместных предикатов  , определённых на произвольном множестве M.
, определённых на произвольном множестве M.
Пусть 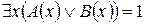 , тогда по определению операции утверждения существования
, тогда по определению операции утверждения существования  для некоторого a из M. Следовательно,
для некоторого a из M. Следовательно, 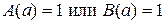 , где
, где  M. Воспользовавшись снова определением операции утверждения существования, получим, что
M. Воспользовавшись снова определением операции утверждения существования, получим, что 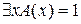 или
или 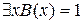 , а, следовательно, истинна и их дизъюнкция
, а, следовательно, истинна и их дизъюнкция  .
.
Пусть теперь  , тогда
, тогда 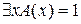 или
или 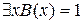 . В первом случае получим, что
. В первом случае получим, что 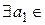 M,
M,  , во втором –
, во втором –  M,
M,  . Однако в обоих случаях существует такой элемент
. Однако в обоих случаях существует такой элемент  M, что
M, что  , в первом случае
, в первом случае  , во втором –
, во втором –  . А это означает, что
. А это означает, что 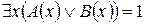 . Ч.Т.Д.
. Ч.Т.Д.
На множестве формул алгебры предикатов можно ввести отношение эквивалентности.
Определение. Формула алгебры предикатов U называется эквивалентной формуле V (обозначается U º V), если их эквиваленция общезначима.
Множество формул алгебры предикатов можно разбить на классы эквивалентности, включив в один класс эквивалентные между собой формулы. Каждой формуле U соответствует класс эквивалентности, который обозначается [ U ].
Определение. Формула алгебры предикатов называется приведенной, если она содержит операции утверждения всеобщности, существования, конъюнкции, дизъюнкции и операцию отрицания, относящуюся к атомарным формулам.
Теорема 3.1. Каждый класс эквивалентности [ U ] может быть представлен приведенной формулой, т.е. для любой формулы U существует эквивалентная ей приведенная формула V.
Для формул алгебры предикатов существуют предваренные нормальные формы.
|
|
|
Определение. Предваренной нормальной формой (ПНФ) формулы алгебры предикатов называется формула, имеющая вид
 ,
,
где  – некоторые кванторы, а U – бескванторная приведенная формула. Выражение
– некоторые кванторы, а U – бескванторная приведенная формула. Выражение  называется префиксом, а U – матрицей нормальной формы.
называется префиксом, а U – матрицей нормальной формы.
Будем говорить, что бескванторная формула U находится в ДНФ(КНФ), если U получается из формулы алгебры высказываний, находящейся в ДНФ(КНФ), подстановкой вместо пропозициональных переменных некоторых атомарных формул.
ПНФ называется пренексной нормальной формой (ПННФ), если её матрица имеет вид ДНФ, и предклазуальной (пкнф), если – КНФ.
Пример. Построим ПН-форму для формулы
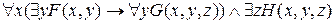 .
.
Преобразуем формулу к приведенному виду
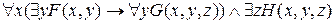 º
º
º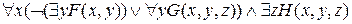 º
º
º .
.
Так как для сочетания квантора " и операции Ú в «Основных общезначимостях» нет соответствующей эквивалентности, то переименуем связанную переменную y второго операнда дизъюнкции и вынесем кванторы по переменным, от которых не зависит другой операнд, вперёд
 º
º
º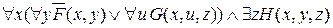 º
º
º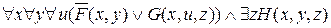 .
.
В первом операнде конъюнкции последней формулы переменные x и y – связанные, а z – свободная, а во втором – наоборот. Переобозначив снова связанные переменные, получим
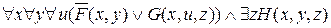 º
º
º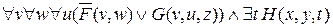 º
º
º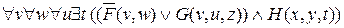 .
.
Полученная предварённая нормальная форма является предклазуальной.
Использование формул алгебры предикатов в информационных технологиях породило необходимость преобразования формул в бескванторные, так как работать с такими формулами значительно легче, чем с формулами, содержащими кванторы. Основой такого преобразования являются аксиомы Скол е ма:
1)  Þ
Þ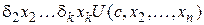 ;
;
2) 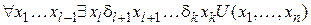 Þ
Þ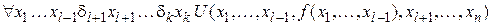 .
.
Здесь с и 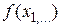 – некоторая константа и функция, специально подбираемые для каждого случая.
– некоторая константа и функция, специально подбираемые для каждого случая.
Возможность удаления кванторов всеобщности непосредственно следует из определения операции, так как  для произвольного x.
для произвольного x.
Формула U находится в клазуальной нормальной форме, если она получена из формулы, находящейся в предклазуальной нормальной форме, удалением кванторов существования в соответствии с аксиомами Сколема и последующим удалением всех кванторов всеобщности. Процесс такого преобразования называется сколемизацией.
|
|
|
Так клазуальная нормальная форма для формулы предыдущего примера имеет вид 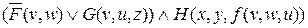 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 541; Нарушение авторских прав?; Мы поможем в написании вашей работы!