Синтез систем логічного управління

Серед різновиду систем управління важливе місце займають системи логічного управління (СЛУ). Характерним признаком цих систем є застосування двійкових датчиків та виконавчих механізмів у вигляді джерел вхідних і приймачів вихідних сигналів. При проектуванні СЛУ широко використовуються типові СІС та БІС, що дозволяють реалізувати апаратним (схемотехнічним) шляхом складні функції й алгоритми. До числа таких СІС відносяться арифметико-логічні, регістрові, рахувальні та тригерні пристрої, суматори множники, мультиплексори, шифратори, компаратори та ін. Менш відомі в практиці проектування такі СІС, як мультиплексори (MX), щo являють собою логічний пристрій, що містить g-управляючих входів U₁, U₂,..., U_g; 2^g інформаційних входів D0, D1,..., D2^g-1, стробуючий вхід та вихід. При подачі на управляючі входи деякої комбінації двійкових сигналів і відповідного сигналу на вхід стробування до виходу Y мультиплексора підключається той інформаційний вхід, порядковий номер якого відповідає вазі двійкової комбінації управляючих сигналів.

Побудова логічних схем на мультиплексорах проводиться у вигляді структур, що відрізняються способами функціонального розділення і розкладення булевих функцій (БФ). Найбільш часто на практиці застосовується розкладання БФ по способу Шеннона:

де - залишкові функції розкладання, що одержуються із функції шляхом підстановки констант 0 і 1 замість змінних множини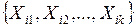

для маємо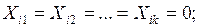

для маємо

для 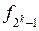_l маємо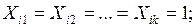

Наприклад, булева функція має вид:

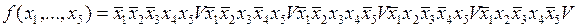
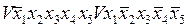
Для компактності представлення заданої булевої функції використовують десяткову форму запису з позначенням нею окремих термів (кон'юнкцій), представивши її у вигляді множини :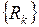

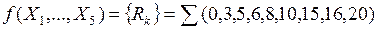
З урахуванням специфіки роботи мультиплексорів і конструктивних особливостей їх реалізації з числом управляючих входів g=2,3,4 та інформаційних входів, рівним 2^g (4,8,16), розкладання заданої БФ можна вести за двома, трьома або чотирма змінними. Тоді при побудові логічної схеми на мультиплексорах змінні повинні підключатись до управляючих входів а залишкові функції (ЗФ) розкладання - до інформаційних входів відповідного MX. Якщо утворені в результаті першого кроку ЗФ мають нетривіальний вид, то процедура розкладання кожної, що одержуємо на черговому кроці залишкові функції, повинна повторюватись до моменту перетворення їх у тривіальні, а саме:

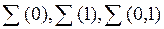0 (відсутня)

Залишкові функції розкладання Q_t по останнім двом 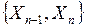, трьом 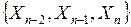, чотирьом 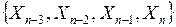змінним з булевої функції можуть бути обчислені за формулами:

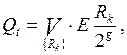
де t=0,1,...,2^g-1;

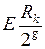- ціла частина від ділення ;

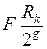- залишок частина від ділення ;

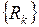- множина термів БФ;

g - число змінних, по яким розкладається БФ.

При побудові логічної схеми на MX, що реалізує задану БФ, можливі два випадки: a) n<=g; б) n>g.

В першому випадку БФ реалізується схемою, що складається з одного мультиплексора, в якому g змінних 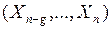підключається до управляючих входів MX, а на інформаційні входи подаються константи 0 (якщо данний терм у функції відсутній) або 1 (якщо він присутній).

В другому випадку процес побудови логічної схеми проводиться за результатами розкладання заданої БФ. Внаслідок першого кроку розкладання вихідної БФ по по g змінним одержуємо сукупність ОФ, що залежать вже тільки від n-g змінних. Наступні кроки розкладання зменшують кожний раз число змінних в ЗФ на g, аж до одержання в процесі розкладання ЗФ тривіального виду. Таким чином, число кроків розкладання БФ відповідає числу каскадів схеми на мультиплексорах з підключенням на управляючі входи MX тих змінних, по яких здійснювалось розкладання; на інформаційні входи MX останнього каскаду подаються окремі змінні або 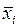, а також сигнали логічного 0 чи логічної 1, виходячи з виду отриманих ЗФ:

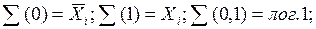Ǿ

Згідно з приведеним вище алгоритмом здійснимо розкладання заданої БФ по двом, трьом та чотирьом змінним, зводячи результати розрахунків у таблиці.

Варіант розкладання БФ по двом змінним наведені у

табл.4.1.

Таким чином, на першому кроці розкладання БФ одержуємо слідуючі ЗФ:

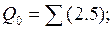
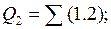
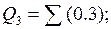
Розкладання БФ продовжимо, так як не всі ЗФ мають тривіальний вид.

На другому кроці у вигляді вихідних даних розглядаються складові кожної з одержаних на першому кроці розкладання залишкові функції Q_t (табл.4.2.).

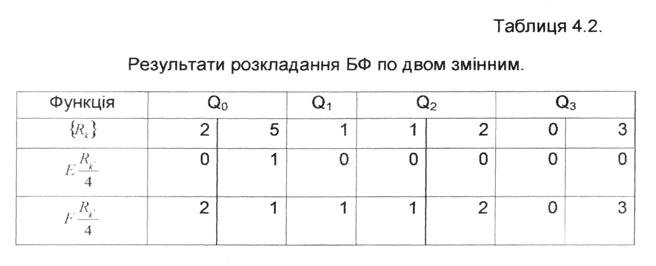
На другому кроці розкладання БФ маємо слідуючи ЗФ:

для Ǿ;

для Ǿ; Ǿ; Ǿ;

для 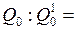Ǿ; Ǿ;

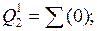
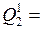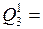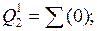
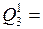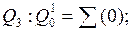
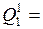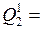для Ǿ; Ǿ;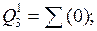

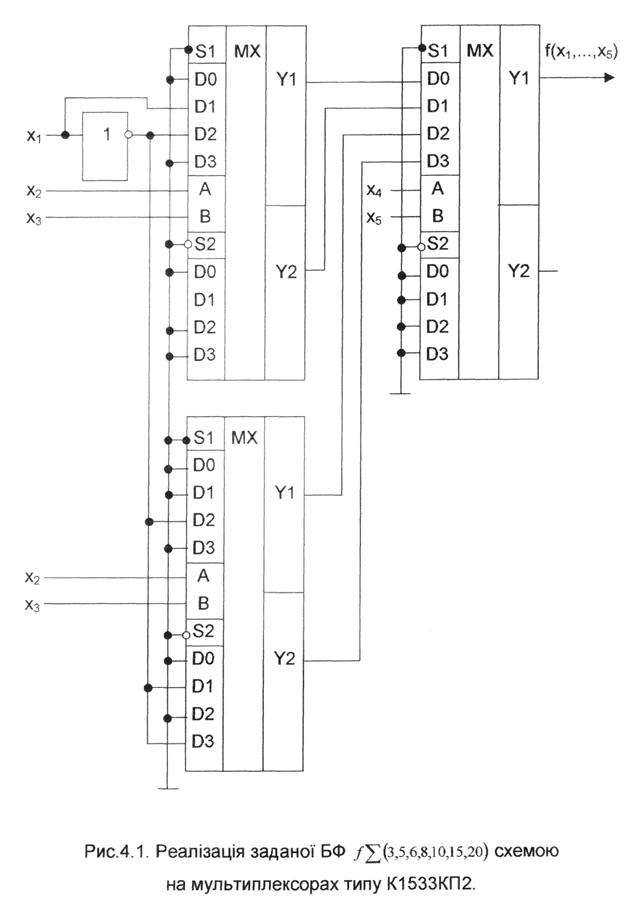
Так як ЗФ, отримані на другому кроці розкладання, є тривіальні, перевіримо до практичної реалізації двокаскадної схеми на MX з g=2. Схемна реалізація БФ на MX типу К1533КП2 наведена на рис.4.1.

Варіант розкладання БФ по трьом змінним наведено в табл.4.3.

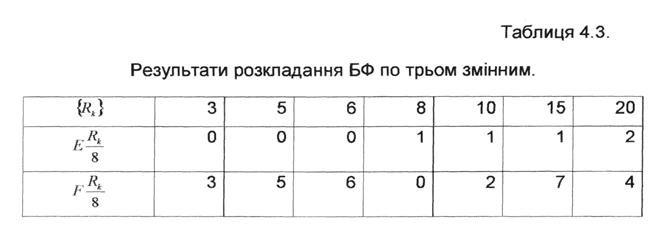
Таким чином, після першого розкладання по трьом змінним отримано наступні ЗФ:

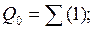
Ǿ;

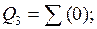
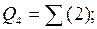
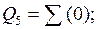
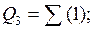
Оскільки одну частину ЗФ отримали тривіальною (Q₀÷Q₁,Q₅÷Q₇), a іншу (Q₄) - нетривіальною, це свідчить про недоцільність подальшого розкладання БФ та її схемної реалізації (для остаточної реалізації БФ при такому підході потрібно вісім мультиплексорів).

Варіант розкладання БФ по чотирьом змінним наведено в табл.4.4.

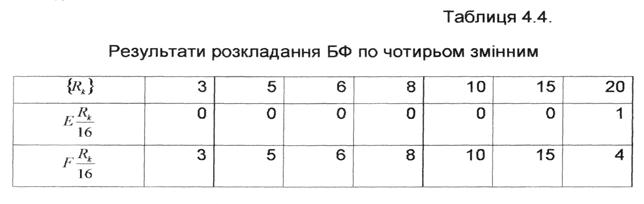
Таким чином, після першого кроку розкладання БФ по чотирьом змінним отримано слідуючі ЗФ:

Q₀=Q₁=Q₂=Q₇=Q₉=Q₁₂=Q₁₃=Q₁₄=Ǿ; Q₃=Q₅=Q₆=Q₈=Q₁₀=Q₁₅= Ǿ;

Q₀=1.

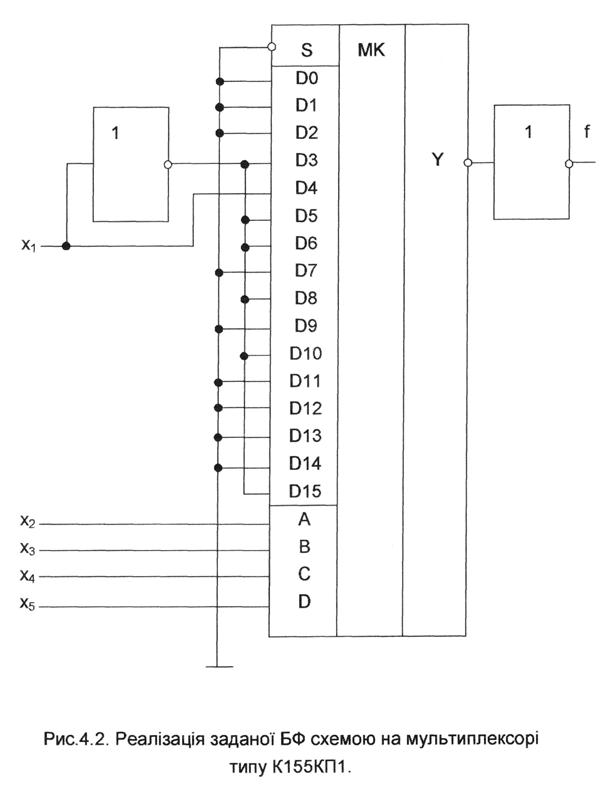
Оскільки всі ЗФ тривіальні, розкладання БФ закінчуємо і її можна реалізувати на одному MX при g=4. Схемна реалізація заданої БФ на одному мультиплексорі типу К155КП1 наведена на рис.4.2.

Для реалізації на мультиплексорах краще всього підходять БФ з числом змінних кон'юнкцій до 9.

Питання для самоконтролю

1. В чому полягає суть розкладання булевих функцій по методу Шеннона?

2. Чому розкладання булевих функцій можна вести за двома, трьома або чотирьма змінними при побудові логічних схем на мультиплексорах?

3. Як можуть бути обчислені залишкові функції?

4. Які випадки можливі при побудові логічних схем на мультиплексорах?

5. За якими правилами ведеться схемна реалізація заданої БФ?

6. Як визначається число каскадів схеми?

7. Які БФ можливо реалізувати на мультиплексорах?

Рекомендована література

1. Арсеньев Ю.Н., Журавлев В.М. Проектирование систем логического управлення на микропроцессорных средствах. -М.: Высшая школа, 1991.

2. Закревский А.Д. Логический синтез каскадних схем. -М., 1981.

3. Юдицкий С.А., Тагаевская А.А., Ефремова Г.К. Проектирование дискретных систем автоматики. - М.: Высш.шк., 1980.

4. Горбатов В.А. и др. Логическое управление технологическими процессами. - М.: Высш.шк., 1978.

Дата добавления: 2014-01-11