Признаки сходимости положительных рядов

Теорема 3. (признак Даламбера) Если в ряде с положительными членами (1) существует конечный предел 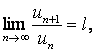то

при l < 1 ряд сходится;

при l > 1 ряд расходится;

при l = 1 признак не применим.

З а м е ч а н и е. Если 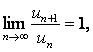но отношение для всех номеров, начиная с некоторого N, то ряд расходится.

Теорема 4. (радикальный признак Коши) Если для ряда с положительными членами (1) существует конечный предел то:

при l < 1 ряд сходится;

при l > 1 ряд расходится;

при l = 1 признак не применим.

Теорема 5. (интегральный признак Коши) Пусть члены ряда (1) положительны и не возрастают, т.е. u ₁ ³ u ₂ ³ u ₃ ³ …

и f (x) – такая непрерывная не возрастающая функция, что

f (1) = u ₁, f (2) = u ₂ , …, f (п) = u_п.

Тогда ряд (1) и несобственный интеграл 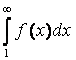одновременно сходятся или расходятся.

Теорема 6. (1-ый признак сравнения) Пусть даны два ряда

(1)

где u_i > 0, v_i > 0. (2)

Если u_n £ v_n (п = 1, 2, …), (3)

то: а) если ряд (2) сходится, то сходится и ряд (1);

б) если ряд (1) расходится, то расходится и ряд (2).

З а м е ч а н и е 1. Данные признаки справедливы только для рядов с положительными членами. Они остаются в силе и для того случая, если некоторые члены 1-го или 2-го ряда – нули. Однако эти признаки перестают быть верными, если среди членов ряда имеются отрицательные числа.

З а м е ч а н и е 2. Теорема 6 справедлива и в случае, если условие (3) начинает выполняться лишь для n ³ N, а не для всех п = 1, 2, 3, …

Теорема 7. (2-ой признак сравнения) Если существует предел

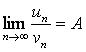(А ≠ 0, А ≠ ∞),

то ряды (1) и (2) одновременно сходятся или одновременно расходятся.

З а м е ч а н и е 3. Сходимость многих рядов можно исследовать путем сравнения их с рядом Дирихле , сходимость которого зависит от параметра р: если 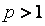, то ряд сходится, если , то ряд расходится.

Знакочередующиеся ряды

◙ Ряд (4)

где u_п ³ 0 (п = 1, 2, …) – называется знакочередующимся.

Теорема Лейбница. Если члены ряда (4) таковы, что:

1) u ₁ > u ₂ > u ₃ > … (монотонно убывают); (5)

2)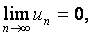 (6)

то ряд (4) сходится и его сумма положительна и меньше u ₁, т.е. 0 < S < u ₁.

З а м е ч а н и е 1. Теорема Лейбница справедлива, если неравенство (5) выполняется, начиная с некоторого N.

З а м е ч а н и е 2. Теорема Лейбница иллюстрируется геометрически.

Если на числовой прямой откладывать частичные суммы (Рисунок 3.3.1):

s₁ = u₁, s₂ = u₁ – u₂ = s₁ – u₂, s₃ = s₂ + u₃, s₄ = s₃ – u₄, …,

то точки, соответствующие частичным суммам, будут приближаться к некоторой точке s, которая изображает сумму ряда. При этом

s₂ < s₄ < s₆ < …< s < …< s₅ < s₃ < s₁.

Рисунок 3.3.1

З а м е ч а н и е 3. (Оценка остатка ряда)

Если знакочередующийся ряд удовлетворяет условию Лейбница, то

– знакочередующийся ряд с первым членом (–1) ^{п +2} и_{п +1}, следовательно, | r_n | < и_{п +1}.

Таким образом, (т.к., s = s_п + r_n) оценка ошибки: | s – s_п | < и_{п +1},

т.е. ошибка, совершаемая при замене s на s_п, не превосходит по абсолютной величине первого из отброшенных членов.

Знакопеременные ряды

◙ Знакопеременный ряд – ряд, среди членов которого имеются как положительные, так и отрицательные.

Знакочередующийся ряд – частный случай знакопеременного ряда.

Пусть дан знакопеременный ряд

(7)

Рассмотрим ряд, составленный из абсолютных величин

(8)

Теорема 8. (Достаточный признак сходимости знакопеременного ряда) Если сходится ряд (8), составленный из абсолютных величин, то сходится и знакопеременный ряд (7).

Дата добавления: 2014-01-11