Свойства абсолютно и условно сходящихся рядов

З а м е ч а н и е. Теорема дает только достаточный признак сходимости знакопеременного ряда, который не является необходимым.

◙ Знакопеременный ряд (7) называется абсолютно сходящимся, если сходится ряд (8), составленный из абсолютных величин его членов.

◙ Если же знакопеременный ряд (7) сходится, а ряд (8) расходится, то данный знакопеременный ряд (7)называется условно (или не абсолютно) сходящимся рядом.

С помощью понятия абсолютной сходимости Теорему 8 формулируют следующим образом: всякий абсолютно сходящийся ряд есть ряд сходящийся.

Теорема 9. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Теорема 10. Если ряд сходится условно, то, какое бы мы ни задали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась равной А. Более того, можно так переставить члены условно сходящегося ряда, что полученный ряд окажется расходящимся.

2. Функциональные ряды

◙ Выражение вида

, (9)

где и_п (х) (n = 1, 2, …) – функции от х, называется функциональным рядом.

При определенных числовых значениях х ряд (9) становится числовым рядом, который может оказаться сходящимся или расходящимся.

◙ Совокупность тех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда.

В области сходимости ряда его сумма является некоторой функцией от х. Поэтому сумму функционального ряда обозначают через s (x).

◙ Сумма называется частичной суммой ряда, а сумма 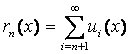называется п -ым остатком ряда.

Если функциональный ряд сходится и сумма его равна s (x), то

s (x) = s_n (x) + r_n (x).

Тогда для любого х из области сходимости имеет место соотношение:

,

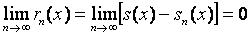т.е. остаток r_n (x) сходящегося ряда стремится к нулю при п ® ¥.

◙ Ряд (9) называется мажорируемым в некоторой области (D) изменения х, если существует такой сходящийся числовой ряд

a ₁ + a ₂ + …+ a_n +…, (a_i > 0) (10)

что " x Î D справедливы неравенства:½ u_i (х)½≤ a_i (i = 1, 2, …).

При этом ряд (10) называется мажорирующим (мажорантным) рядом.

◙ Степенным рядом (по степеням х) называется функциональный ряд вида а ₀ + а ₁ х + а ₂ х ² + … + а_п х^п + … (11)

где а_i (i = 0, 1, 2, …) – коэффициенты степенного ряда (постоянные числа).

Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.

Теорема 11. (теорема Абеля)

1) Если степенной ряд сходится при некотором х ₀ ¹ 0, то он абсолютно сходится при " х: ½ х ½< х ₀;

2) Если степенной ряд расходится при некотором х ₀, то он расходится при " х: ½ х ½> х ₀.

Теорема 12. Областью сходимости степенного ряда является интервал с центром в 0.

◙ Интервалом сходимости степенного ряда называется такой интервал (– R, R), что при всех х Î(– R, R) ряд (11) сходится и притом абсолютно, а при всех ç х ç> R ряд (11) расходится. Число R называют радиусом сходимости степенного ряда.

На концах интервала (т.е. при х = ± R) вопрос о сходимости или расходимости решается индивидуально.

Если R = ∞, то интервалом сходимости степенного ряда является вся числовая прямая, если R = 0, то интервал сходимости вырождается в точку.

Число R вычисляется по формулам: или ,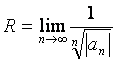

которые легко получить, воспользовавшись соответственно признаком Даламбера или радикальным признаком Коши.

Степенные ряды можно почленно дифференцировать и интегрировать в их интервалах сходимости. Радиус сходимости при этом не изменяется.

В общем случае степенной ряд (по степеням (х – х ₀)) имеет вид:

,

где постоянные а_п (п = 1, 2, …) также называются коэффициентами ряда.

Интервалом сходимости такого ряда является интервал (х ₀ – R; х ₀ + R) с центром в точке х ₀. Число R – радиус сходимости ряда – вычисляется, как и прежде.

Дата добавления: 2014-01-11