
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рекуррентные вычисления и обработка сигналов
|
|
|
|
End.
Begin
Begin
Примеры рекуррентных вычислений
Пример 1. Вычислить n -ое число Фибоначчи.
k=2, поэтому буфер состоит из 3-х переменных t1, t2, t3.
Function Fib (n:Integer):Integer;
Var t1, t2, t3, i:Integer;
t2:=1; t3:=1; { начальная установка буфера}
For i:=3 To n Do Begin
t1:=t2; t2:=t3; { сдвиг буфера}
t3:=t1 + t2; { вычисление нового элемента}
End;
Fib:= t3;
End;
Пример 2. Вычислить значение многочлена при заданном х.
c0xm + c1xm-1 +… + cm
Сразу рекуррентные зависимости здесь не видны, однако, если воспользоваться схемой Горнера, то получим:
(…(( c0x + c1) x + c2) x + …) x + cm
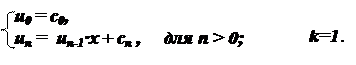 Алгоритм:
Алгоритм:
Var c: Array [0..m] Of Real; { массив коэффициентов с }
sp, st: Real; { буфер}
…………………………………………………………
1-ый вариант:
st:= c[0];
For i:= 1 To m Do Begin
 sp:= st; { сдвиг буфера}
sp:= st; { сдвиг буфера}
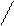 st:= sp*x + c[i]; { вычисление нового элемента}
st:= sp*x + c[i]; { вычисление нового элемента}
end;
2-ой вариант: - можно обойтись одной переменной s.
s:= 0;
 For i:= 0 To m Do s:= s*x + c[i]; {результат накапливается в s}
For i:= 0 To m Do s:= s*x + c[i]; {результат накапливается в s}
автоматически формирует Sнач
3.2. Двумерные рекуррентные вычисления.
Рассмотрим применение 2-мерных рекуррентных вычислений.
| C 0 1 2 3 4 5 6 7 | ||||||||
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 |
что (i, j) - элемент треугольника Паскаля есть число сочетаний из i по j:
 - определяет сколько можно образовать подмножеств из k
- определяет сколько можно образовать подмножеств из k
элементов, если задано множество из n элементов
Пример 1.. Требуется напечатать первые строки треугольника Паскаля [6] с нулевой по n. Если через c (i, j) обозначить число, стоящее в i - й строке на j -м месте, то по определению треугольника Паскаля справедливы соотношения:
|
|
|
c i,0 = c i, i = 1;
c i, j = c i -1, j-1 + c i -1, j, i ≥ 0, 0 < j < i
1 вариант. Если буквально воспользоваться определением треугольника Паскаля, получается следующая процедура:
Var С: Array [0..n-1, 0..n-1] Of Integer;
……………………………………………………………..
For i:=0 To n-1 Do Begin
C[ 1, i ]:= 1; C[ i, i ]:= 1;
For j:=1 To i -1 Do
C [ i, j ]:= C [ i -1, j -1 ] + C [ i -1, j ];
End;
Вывод матрицы С.
2 вариант. Подумаем, как уменьшить объем необходимой памяти. При вычислении очередной строки используются не все ранее найденные элементы треугольника, а только предыдущая строка. Печатать строки треугольника можно не в конце программы, а по мере их вычисления. Значит, достаточно двух одномерных массивов, в которых по аналогии с рекуррентной последовательностью первого порядка будут вычисляться строки треугольника. Чтобы избежать лишних копирований массивов, заведем указатели на массивы p и t, значения которых будем попеременно обменивать.

Type tm = Array [ 0..n -1] Of Integer;
Var p, t:^tm;
New (p); New (t);
p^[0]:= 1; {первый элемент в всегда в 1}
For i:= 0 To n -1 Do Begin
t^[i]:=1; {диагональный элемент всегда в 1}
For j:= 1 To i -1 Do
t^[j]:= p^[ j -1] + p^[ j ];
Вывод t^;
Обмен p и t;
End;
Dispose(p); Dispose(t);
Процедура усложнилась, но и экономия памяти по сравнению с предыдущим вариантом существенная: в массивах хранится 2n чисел вместо n×n.
3 вариант. Можно, однако, уменьшить расход памяти еще в два раза, если обойтись одним одномерным массивом и вычислять очередную строку треугольника Паскаля на месте предыдущей. Элементы строки целесообразно вычислять справа налево, чтобы изменять значения только тех компонент массива, которые в дальнейшем не понадобятся.

Var t:tm;
…………………………………………………………………..
For i:= 0 To n – 1 Do Begin
t [ i ]:= 1; { при i = 0 → t [ 0 ] = 1 }
For j:= i - 1 DownTo 1 Do t [ j ]:= t [ j – 1 ] + t [ i ];
Вывод t;
End;
По сравнению с первоначальным вариантом мы не только сократили расход памяти, но и получили более изящную процедуру.
|
|
|
Конечно, наибольший эффект получается тогда, когда удается по-новому посмотреть на поставленную задачу. Но и следование несложному правилу — потреблять информацию сразу после ее получения — способно существенно снизить расход памяти.
| Матрица А | ||||||
| i/j | 1 | |||||
| 1 | ||||||
Пример 2. В матрице А c n строками и m столбцами, состоящей из 0 и 1, необходимо найти квадратный блок максимального размера, состоящий из одних единиц. Под блоком понимается множество элементов соседних (подряд идущих) строк и столбцов матрицы. Интересующая нас часть показана на рисунке.
| Таблица значений T(i,j) Матрица В | ||||||
| i/j | 1 | |||||
| 1 | ||||||
Положение любого квадратного блока может быть определено его размером и положением одного из его углов. Пусть T(i, j) есть функция, значение которой соответствует размеру максимального квадратного блока, состоящего из одних единиц, правый нижний угол которого расположен в позиции (i, j) . Функция T (i, j) вычисляет элемент матрицы B [i, j]. На следующем рисунке показаны значения T (i, j).
Таким образом, наша задача свелась к вычислению максимального значения функции Т при всевозможных значениях параметров i и j. Этой функции может быть поставлена в соответствие таблица размера n · m .
Определим сначала значения элементов матрицы В , расположенных в первой строке и в первом столбце. Получим:
В [1, 1] = А [1, 1],
В [1, j] = А [1, j] при j ≥2,
В [i, 1] = A [i, 1] при i ≥2.
Эти соотношения следуют из того факта, что в этих случаях рассматриваемая область матрицы А содержит только один элемент матрицы.
При 2 ≤ i ≤ n и 2 ≤ j ≤ m для этой функции можно записать следующие рекуррентные соотношения:
B [i, j] = 0, если A [i, j] = 0 и
B [i, j] = Min (B [i - 1, j], B [i, j - 1], B [i - 1, j - 1]) + 1, если A[i, j] = 1.
Первое соотношение показывает, что размер максимального единичного блока с правым нижним углом в позиции (i, j ) равен нулю в случае A [i, j] = 0. Убедимся в правильности второго соотношения. Действительно, величина B [i - 1, j] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i - 1, j ). Тогда размер единичного блока с правым нижним углом в позиции (i, j ) не превышает величину B [i - 1, j] + 1, так как к блоку в позиции (i - 1, j ) могла добавиться только одна строка. Величина B [i, j - 1] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i, j - 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j ) не превышает величину B [i, j - 1] + 1, так как к блоку в позиции (i - 1, j ) мог добавиться только один столбец. Величина B [i - 1, j - 1] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i - 1, j - 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j ) не превышает величину B [i - 1, j - 1] + 1, так как к блоку в позиции (i - 1, j - 1) могли добавиться только одна строка и один столбец. Итак, размер единичного блока с правым нижним углом в позиции (i, j ) равен Min ( B [i - 1, j], B [i, j - 1], B [i - 1, j - 1]) + 1.
|
|
|
…………………………………
В[1, 1]: = A[1, 1];
For j:=2 To 6 Do В[1, j]: = A[1, j];
For i:= 2 To 5 Do В[i, 1]: = A[i, 1];
For i:=2 To 5 Do
For j:=2 To 6 Do
If A[i, j]: = 1
Then B[i, j]: = Min (B[i - 1, j - 1], B[i, j - 1], B[i - 1, j]) + 1;
Else B[i, j]: = 0;
…………………………………..
Замечание. Рассмотренные варианты вычисления треугольника Паскаля носят скорее учебный характер. Но и на практике рекуррентные схемы вычислений и организации данных находят широкое применение – особенно в области обработки изображений. Например [10], известная операция выделения на изображении «скелета» может быть сведена к рекуррентным вычислениям, подобным рассмотренными в варианте 2, однако различие состоит в том, что значение t^[ j ] есть функция не только от p^[j-1] и p^[j], но и от t^[ j-1 ]:
t^[ j ] = F (p^[j-1], p^[j], t^[ j-1 ]).
В данном случае возможна следующая модификация рассмотренной схемы вычислений. Пусть вместо динамических используются статические массивы. Чтобы избавиться от второго буферного массива p вводятся две дополнительные одиночные переменные a и b. Все вычисления в данный момент времени производятся в окне вычислений.  Обозначим как с и d элементы окна - t]j-1] и t[j] соответственно. На самом деле, если бы использовались два буфера они в данный момент времени хранили бы информацию соответствующую p[j-1] и p[j]. Перемещая информацию надлежащим образом в окне вычислений удается и здесь сократить объем необходимой памяти. Схема вычислений приведена ниже:
Обозначим как с и d элементы окна - t]j-1] и t[j] соответственно. На самом деле, если бы использовались два буфера они в данный момент времени хранили бы информацию соответствующую p[j-1] и p[j]. Перемещая информацию надлежащим образом в окне вычислений удается и здесь сократить объем необходимой памяти. Схема вычислений приведена ниже:
|
|
|
For i:= 0 To n -1 Do Begin {перебор строк изображения}
a:= 0;
For j:= 1 To n - 1 Do Begin {просмотр буфера t}
b:= a; { b:= t[j-1] }
a:= F (с, d, b); { вычисление нового значения }
c:=b;
End;
Вывод t;
Еnd;
Приемы, характерные для обработки рекуррентных вычислений, как уже отмечалось, широко используются на практике. Рассмотрим несколько примеров из области обработки сигналов. Первый из них относится к обработке одномерных сигналов. Аналоговый сигнал какого-либо физического процесса после квантования и дискретизации часто представляется в виде одномерного массива значений (рис.3.1).

Массивы эффективно обрабатываются на ЭВМ:
- хорошо отображаются в одномерную память;
- есть прямой доступ к элементам;
- имеется аппаратная поддержка обработки (цепочечные и специализированные
машинные команды, способы адресации);
- эффективно обрабатываются циклами For.
Часто процедура обработки сигнала сводится к следующей вычислительной схеме. Имеется окно вычислений b (логически выделяется в массиве а или резервируется отдельно), которое сканируется вдоль массива а. Обычно m<<n. Для каждого положения окна вычисляются значения некоторой функции окна F (a,b), в соответствии с решаемой задачей, например:
- фильтрация сигнала;
- корреляция;
- определение совпадающих фрагментов;
- пороговое преобразование;
- и т. п.
Рассмотрим обработку сигнала усредняющим фильтром. Пусть результаты фильтрации записываются в массив r.
For i:= 0 To n - m Do Begin {цикл сканирования окном}
s:= 0;
For j:= 0 To m-1 Do s:= s + a[ i + j ]; {накопление суммы в пределах окна}
r [ i + m Div 2 ]:= s Div m; {запись среднего значения}
End;
Если не учитывать краевых эффектов (связанных с неопределенностью на концах массива r), то основное требование к алгоритму – максимальное быстродействие. Количество основных операций равно:
V = (n - m+1)*(m + 1),
где: (n - m+1) – количество повторений внешнего цикла;
(m+1) – количество повторений внутреннего цикла плюс операцияделения.
 Учитывая, что m<<n
Учитывая, что m<<n
V ≈ n* m.
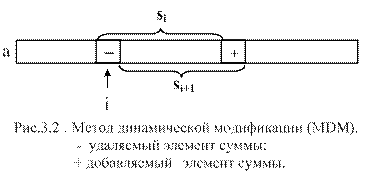
Однако, можно заметить, что одни и те же слагаемые входят в суммы для соседних положений окна. Поэтому можно применить, так называемый метод динамической модификации (MДМ), повышающий эффективность вычислений (рис.3.2.). Рекуррентная формула для получения значения следующей суммы выглядит следующим образом: si+1 = si + ai+m - ai.
Тогда МДМ – алгоритм можно представить в следующем виде:
s:=0;
For i:= 0 To m -1 Do s:= s + a [ i ]; {вычисление 1-ого значения}
r [ m Div 2 ]:= s;
For i:= 1 To n - m Do Begin
s:= s + a [ i + m – 1] – a [ i –1] { MDM –
r [ i + m Div 2 ]:= s Div m; вычисления }
End;
Объем вычислений V ≈ n и не зависит от n.
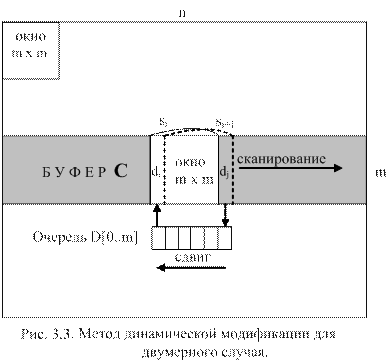 Подобные приемы повышения эффективности вычислений можно применять и для двумерных сигналов, например изображений (рис. 3.3). «Лобовое» решение задачи фильтрации на двумерном изображении размером n×n c окном m×m дает объем вычислений порядка V ≈ n2∙m2. При этомобъемтребуемой оперативной памяти под изображение составляет n×n байт (в предположении, что под пиксель отводится один байт). Организация МДМ – вычислений может быть реализована в двух вариантах.
Подобные приемы повышения эффективности вычислений можно применять и для двумерных сигналов, например изображений (рис. 3.3). «Лобовое» решение задачи фильтрации на двумерном изображении размером n×n c окном m×m дает объем вычислений порядка V ≈ n2∙m2. При этомобъемтребуемой оперативной памяти под изображение составляет n×n байт (в предположении, что под пиксель отводится один байт). Организация МДМ – вычислений может быть реализована в двух вариантах.
1 вариант. Выделим буфер B (см. рис.3.3) размером m×n и вначале загрузим в него первые m строк изображения. Для фильтрации этого фрагмента изображения
окно m×m сканируется вдоль буфера B. Значение суммы для каждого положения окна вычисляется по формуле si+1 = si + dj - di, где dj - сумма элементов
| b1 | b2 | b3 | ||||
| b0 | c | b4 | ||||
| b7 | b6 | b5 | ||||
Если 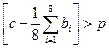 , то , то 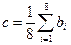 Рис.3.4.Пример алгоритма
подавления шума
Рис.3.4.Пример алгоритма
подавления шума
|
поступающего в окно столбца и di - сумма элементов первого столбца окна в предыдущем положении. После прохождения окном всего буфера B последний сдвигается на одну строку вниз и дополняется снизу новой строкой изображения и процесс сканирования окном повторяется. Сдвиг изображения в буфере B достаточно трудоемкая операция, связанная с перемещением большого объема информации, поэтому желательно не перемещать информацию, а свести сдвиг к манипуляциям с указателями и индексами, так как это обычно применяют к структурам типа «очередь» (см. п. 5.8). Таким образом, приходим к идее кольцевого буфера, в котором используются индекс u для указания начальной строки фрагмента изображения, помещенного в данный момент в буфер. В этом случае сдвигу изображения будет соответствовать изменение этого индекса по закону:
u:= (u +1) mod m;
Буфер называется кольцевым, поскольку значения индекса u изменяются по закону 0,1, …, m -1, 0, 1,...
В данной схеме вычислений можно заметить, что элементы одного и того же столбца суммируются дважды: первый раз при вычислении величины di и второй раз – dj. Чтобы избежать двойного суммирования в структуру данных включается второй кольцевой буфер d (см. рис. 3.3) с указателем (индексом) h на выпадающий при сдвиге элемент буфера. Сдвигу буфера d соответствует изменение индекса h:
h:= (h +1) mod m.
На практике применяются различные фильтры для подавления помех на изображениях. Выбор фильтра зависит от многих причин и во многом от вида помех. Изображение может повреждаться шумами и помехами различного происхождения, например шумом видеодатчика, шумом зернистости фотоматериалов и ошибками в канале передачи. Их влияние можно минимизировать, пользуясь классическими методами пространственной обработки изображений[12].
Шумы видеодатчиков или ошибки в канале передачи обычно проявляются на изображении как разрозненные изменения изолированных элементов, не обладающие пространственной корреляцией. Искаженные элементы часто весьма заметно отличаются от соседних элементов. Это наблюдение послужило основой для многих алгоритмов, обеспечивающих подавление шума [12]. Поскольку шум пространственно декоррелирован, в его спектре, как правило, содержатся более высокие пространственные частоты, чем в спектре обычного изображения. Следовательно, простая низкочастотная пространственная фильтрация может служить эффективным средством сглаживания шумов.
Рис. 3.4 поясняет простой пороговый метод подавления шума, при использовании которого последовательно измеряют яркость всех элементов изображения. Если яркость данного элемента превышает среднюю яркость группы ближайших элементов на некоторую пороговую величину p, яркость элемента заменяется на среднюю яркость. Рис. 3.5 иллюстрирует эффективность этого алгоритма применительно к различным изображениям.
В качестве примера рассмотрим применение МДМ-вычислений для фильтрации бинарного (черно-белого) и полутонового изображений. Эти изображения отличаются тем, что в первом пиксели могут принимать значения 0 или 1, а во втором – в некотором диапазоне кодирования уровня яркости, например, 0..255. Пусть на изображениях присутствуют точечные помехи, искажающие яркости отдельных пикселей (шум типа «соль и перец»). Примеры таких изображений приведены на рис. 3.5. Реализации усредняющего фильтра для бинарного и полутоновых изображений несколько отличаются: в случае бинарных изображений суммарная яркость в окне m×m сравнивается с некоторым априорно заданным порогом p (обычно выбирают p = 0.5 m2), для полутоновых изображений вычисления производятся по формуле на рис. 3.4.
Таким образом, алгоритм фильтрации состоит из следующих основных шагов:
1. Начальная загрузка буфера В первыми m строками изображения.
2. Цикл обработки всего изображения, состоящий из:
а) вычисления первой суммы для начального положения окна в буфере В, вычислений сумм столбцов и начального заполнения буфера d и запись первого отфильтрованного пикселя в результирующий буфер R;
б) сканирования окном m×m буфера В и запись результатов фильтрации в буфер R, при этом используются МДМ-вычисления и ротация значений сумм столбцов в кольцевом буфере d;
в) по завершению сканирования результат (т.е. строка отфильтрованного изображения) из буфера R выводится в выходной файл, а из входного файла в буфер B по индексу u считывается очередная строка исходного изображения.
Ниже приведен пример процедуры Filtr для обработки бинарного изображения с предварительным описанием необходимых структур данных. Результаты обработки бинарного и полутонового изображений приведены на рис. 3.5.
Const n = 250; { размер строки изображения }
m = 7; { m×m – размер окна фильтра }
m0 = m Div 2; {положение центра окна}
p = m*m0; {порог для фильтра}
Type Tstr = Array [0..n-1] Of Byte; {тип строки буфера}
TBuf = Array [0..m-1] Of Tstr; { тип буфера }
Var B:TBuf; { кольцевой буфер n×m для изображения }
d: Array [0..m-1] Of Integer; { кольцевой буфер для сумм столбцов окна }
fi, fo: File Of Tstr; {входной и выходной файлы изображения}
R:Tstr; { буфер вывода строки}
Procedure Filtr; {Процедура фильтрации бинарного изображения
усредняющим фильтром }
Var u, h, {u, h – указатели для буферов}
i, x, s,:Integer; { рабочие переменные}
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 545; Нарушение авторских прав?; Мы поможем в написании вашей работы!