Параметры состояния

Свойством или физической характеристикой системы называется любая измеряемая характеристика изучаемой системы (какого-то объема жидкости). Если две системы проявляют одни и те же свойства, так что они неразличимы, то говорят, что они находятся в одном и том же состоянии.

Состояние характеристик движущейся жидкости определяется значениями параметров состояния окружающей среды. Наиболее удобными, а потому и наиболее распространенными параметрами состояния являются температура и давление. При этих заданных параметрах состояния определяются физические характеристики жидкости. Рассмотрим некоторые характеристики жидкости, необходимые для решения задач гидравлики.

Гипотеза сплошной среды приводит к понятию плотности для тел, находящихся в твердом, жидком или газообразном состоянии. Распределение массы жидкости в объеме характеризуется средней плотностью ρ – массой жидкости, приходящейся на единицу объема

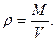
Здесь M – масса жидкости, содержащаяся в объеме V. При неравномерном распределении вещества по объему весь объем разбивается на столь малые объемы 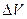, что распределение массы Δ M можно полагать в нем равномерным и местная плотность – плотность в данной точке, определяется пределом:

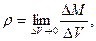кг/м³

Обратная величина называется удельным объемом

,

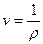где v – удельный объем, т.е. объем, занимаемый единицей массы жидкости или газа.

Состояние газа в любой точке определяется тремя параметрами состояния – давлением p, плотностью и температурой T, которые в случае совершенного газа связаны между собой уравнением состояния Клапейрона – Менделеева:

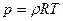. Здесь R – газовая постоянная.

Как уже упоминалось ранее, основной особенностью газа, с которой связано большинство его характерных свойств, заключается в том, что молекулы газа находятся на большом удалении друг от друга и каждая молекула с динамической точки зрения изолирована от других молекул в течение времени свободного пробега, на длине свободного пробега. При температуре 0˚ C и давлении 10⁵ Па число молекул в одном кубическом сантиметре газа равно 2,69 10¹⁹ (оно называется числом Лошмидта, а тот факт, что оно одинаково для всех газов, известен как закон Авогадро), поэтому, если бы молекулы были размещены в углах кубической решетки, расстояния между соседними молекулами было бы 3,3·10^-7 см. Диаметр молекулы точно не определен, однако его обоснованной мерой служит расстояние между центрами двух отдельных молекул, на котором межмолекулярная сила меняет знак. Для многих простых молекул этот эффективный диаметр находится в интервале d ₀=(3 – 4)·10^-8 см, так что средняя величина удаления молекул друг от друга составляет величину порядка 10 d ₀. На этом расстоянии силы сцепления молекул столь малы, что большую часть своей жизни молекулы движутся свободно по прямым линиям с постоянной скоростью (полагаем, что они электрически нейтральны). Среднее расстояние, проходимое молекулой между столкновениями равно 7·10^-6,см или 200 d ₀.

Представление о газе как о скоплении молекул, движущихся почти свободно, исключая случайные столкновения, лежит в основе кинетической теории газов. В этой теории принято рассматривать свойства совершенного газа, молекулы которого не оказывают никакого силового воздействия друг на друга, не считая актов столкновений, и занимают пренебрежимо малый объем. При нормальных условиях реальные газы обладают свойствами, которые мало отличаются от свойств совершенного газа.

При больших плотностях на динамическое поведение молекул влияют расположенные поблизости другие молекулы, уравнение состояния для совершенного газа нуждается в уточнении. Уточненное уравнение состояния называется уравнением Ван-дер-Ваальса

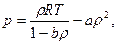
где опытные значения коэффициентов для воздуха приблизительно равны 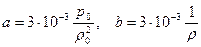, причем значения берутся при стандартных условиях. Это уравнение непригодно для газов вблизи точки конденсации.

При очень высоких температурах столкновения между молекулами могут стать настолько интенсивными, что может происходить диссоциация многоатомных молекул на отдельные атомы. Поэтому уравнение Клапейрона – Менделеева также нуждается в уточнении на состав газа.

Хотя жидкости обладают общим с газами свойством текучести и способностью к свободному изменению формы, существование интенсивных сил сцепление под действием которых находятся молекулы жидкости, не позволяет иметь никакой простой модели, связывающей давление, плотность и температуру подобно модели совершенного газа с динамически независимыми молекулами. Поэтому способность жидкостей изменять свою плотность (объем) оценивается с помощью коэффициентов, определяемых опытным путем.

Сжимаемость жидкости – это свойство жидкости изменять свой объем при изменении давления количественно характеризуется коэффициентом объемного сжатия b_v: .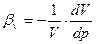

При равномерно распределенной по объему V плотности ρ жидкости в соо-тветствии с законом сохранения массы жидкости в рассматриваемом объеме при изменении объема масса его не изменяется .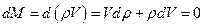

Поэтому 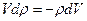и .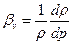

Считая b_v постоянным и записывая в конечных разностях, получим формулу для объема жидкости V при увеличении давления на Dp:

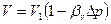и для плотности 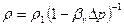. Здесь Dp=p - p₁,.

Модуль объемной упругости K является обратной величиной коэффициента объемного сжатия. Для воды при нормальных условиях модуль упругости равен 2000 МПа; при повышении давления до 10 МПа ее плотность повысится всего на 0.5 % (плотность рабочих жидкостей гидравлических систем – не более чем на 1%). Поэтому в большинстве случаев капельные жидкости можно считать несжимаемыми, т.е. считать плотность жидкости постоянной. Для несжимаемой жидкости уравнение состояние имеет вид r= const.

Однако при очень высоких давлениях и неустановившихся движениях жидкости ее сжимаемость необходимо учитывать. Так, если бы вода в Мировом океане (средняя глубина 3704 м) была несжимаемой, ее уровень повысился бы на 27 м. Класс кремнийорганических жидкостей (силиконы) расширяет диапазон значений модуля упругости до 800 МПа, что позволяет создать на их базе системы, позволяющие аккумулировать энергию в три раза больше, чем с помощью стальных пружин.

Изменение объема жидкости (плотности) при изменении температуры характеризуется коэффициентом температурного расширения b_t: .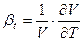

В конечных разностях, получим: .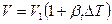

Для воды при нормальных условиях коэффициент температурного расширения b_t =14·10^-6, для минеральных масел имеет порядок 800·10^-6.

Дата добавления: 2014-01-11