Без ограничений

Дана некоторая функция f(х) на открытом интервале (а,в) изменения аргумента х. Предполагаем, что exst внутри этого интервала существует (нужно сказать, что в общем случае математически заранее это утверждть не могут; однако в технических приложениях очень часто наличие exst внутри некоторого интервала изменения интервала изменения аргумента может быть предсказано из физических соображений).

Определение exst. Функция f(x) заданная на интервале (а,в) имеет в точек x^* max(min), если эту точку можно окружить таким интервалом (x^*-ε, x^*+ε),содержащимся в интервале (а,в), что для всех ее точек х, принадлежащих интервалу (x^*-ε, x^*+ε), выполняется неравенство:

f(x) ≤ f(x^*) → для max

f(x) ≥ f(x^*) → для min

Это определение не накладывает никаких ограничений на класс функций f(x), что, конечно, очень ценно.

Если ограничится для функций f(x), достаточно распространенным, но все же более узким классом гладких функций (под гладкими функциями мы будем понимать такие функции, которые непрерывны вместе со своими производными на интервале изменения аргумента), то можно воспользоваться теоремой Ферма, которая дает необходимые условия существования exst.

Теорема Ферма. Пусть функция f(x) определена в некотором интервале (а,в) и в точке «с» этого интервала принимает наибольшее (наименьшее) значение. Если существует в этой точке двухсторонняя конечная производная , то существования необходимо exst .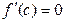

Примечание. Двухсторонняя производная характеризуется свойством

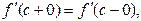
Иными словами, речь идет о том, что в точке «с» производная в пределе одна и та же при подходе к точке «с» слева и с права, т.е. f(x) – гладкая функция.

^*В случае 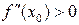имеет место min, а при 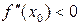→ max. Наконец, если при х=х₀ , то использования 2-ой производной не помогает и нужно воспользоваться, например, определением exst.

При решении задачи I необходимые условия exst (т.е. теорема Ферма) используется очень часто.

Если уравнение exst 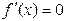имеет вещественные корни, то точки, соответствующие этим корням. Являются подозрительными на exst (но не обязательно самыми экстремумами, ибо имеем дело с необходимыми, а не с необходимыми и достаточными условиями). Так, например, в точке перегиба Х_п имеет место 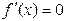, однако, как известно, это не эстремум.

Заметим ещё, что:

а) Из необходимых условий нельзя сказать какой вид экстремума найден max или min: для определения этого нужны дополнительные исследования.

б) Из необходимых условий нельзя определить –глобальный это экстремум или локальный.

Поэтому, когда находят точки подозрительные на exst, их дополнительно исследуют, например, на основе определения exst или 2-ой производной.

Пример(*).

Определить exst функции на открытом интервале (0,2).

По теореме Ферме находим необходимые условия exst функции.

откуда

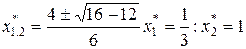
Имеем две точки подозреваемые на exst. Что определить, что мы имеем в каждом случае max, min или точку перегиба необходимо дополнительно исследовать подозрительные точки на основе определения exst.

Исследуем 1-ую подозрительную точку 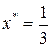. Допустим 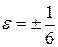вычислим . А теперь получим

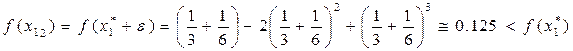Согласно определению exst точка 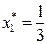соответствует max функции f(x).

Теперь возьмем вторую производную 2-ую подозрительную точку . Пусть ε=±0.1.

Вычислим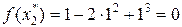

Затем получим

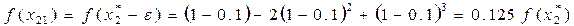
т.е. при 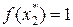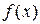имеет min.

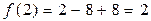
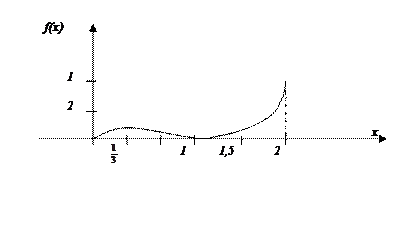
Было бы важно, если заранее можно сказать: «имеет ли рассматриваемая функция единственныйmin (max). Математически установили, что это можно определить, базируясь на понятиях выпуклой (вогнутой) функции.

Существует много определений выпуклости функции, рассмотрим один из них, связанный с касательной к изучаемой функции.

Выпуклой функцией мы будем называть такую функцию, все значения которой ≥ соответствующих значений касательной, проведенной к этой функции в любой её точке. Иными словами выпуклая функция расположена выше любой свой касательной. Уравнение касательной можно записать в общем случае в виде:

, т.е.

Это можно получить их заштрихованного треугольника. Согласно определению выпуклой функции

.

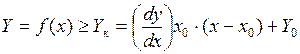Для вогнутой функции картина будет противоположная

.

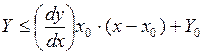Пример. Определить: выпуклая или вогнутая функция 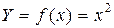, соласно вышеприведенной формуле:

или

; (ибо ).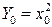

Тогда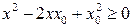

т.е.

Функция 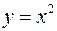-выпуклая

Следовательно, если функция 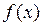-выпуклая, то на интервале (а, в) она имеет единственный min, а если вогнутая, то единственный max.

Задача нахождения экстремума функций одной переменной

Дата добавления: 2014-01-11