C ограничениями

Функция 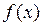задана на ограниченном отрезке [а, в]. Рассмотрим прежний пример (*) (стр. 18)

Здесь уже необходимо включить точки 0 и 2. В этом случае max или min может быть не только внутри, но и на границах, поэтому решают сначала задачу 1, т.е. ии сравнивают с внутри интервала и выбирают max или min.

В нашем случае являются SUP. А относительно min или inf можно сказать, что → inf.

Зато в этом случае есть мощная теорема Вейерштрасса, которой нет в 1.

Функция 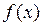, заданная на отрезке [а, в] хотя бы дин раз принимает на нем свое наибольшее и наименьшее значения.

Эта теорема даёт основание утверждать, что линейная или монотонная функция на [а, в] хотя бы один раз принимает SUP и inf, а в случае решения не было – extr не существует.

Пример. Задача замены катализаторов P –доход от работы катализатора (реактора)

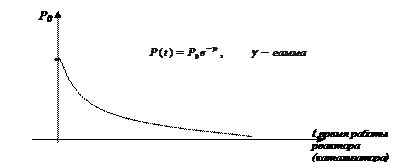
Видно, что с течением времени эффективность работы катализатора снижается и доход падает. Значит, в какой то момент времени надо сменить катализатор, что связано с остановкой реактора. Что в свою очередь дает свои потери. Следовательно, есть оптимальный момент времени, когда выгодно сменить катализатор. Составим функцию - средний доход

, где

R - стоимость катализатора + потери от простоя;

t - текущее время работы катализатора, до его смены;

T- время постоя.

Обычно 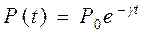откуда

Пример для простоты 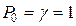, , 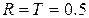тогда

Имеет ли А(t) extr?

Интервал 0,t - не фиксирован, т.е. интервал .

Возьмем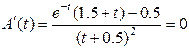

^.

Это можно решить графически – построить левую и правую части уравнений. Если есть их пересечение, то значит, есть корень, т.е. подозрительная точка на extr.

В другом конкретном случае, поскольку

, то можно просто строить 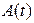, не беречь её производную.

В начале был участок т.к. окупалась стоимость катализатора и работ.

Решение на этом не кончается, надо проверить устойчивость решения к изменению (которое может быть случайное для разных катализаторов).

Мы брали =1, а может быть разброс . Для этих 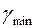и 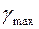снова решать задачу и посмотреть сильно ли изменяется 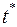. Ели меняется подтверждать (именно понимается здесь термин «устойчивость»-т.е. малому изменению коэффициентов должно соответствовать малое изменение результата). Т.к. кривая в районе extr сильно пологая, то чувствительность к изменению параметров здесь невелика т.е. велика устойчивость (обычно так и бывает). Ели extr острый, то наоборот.

Т.к. функции обычно сложные, то важное значение приобретают методы приближенного нахождения функции одной или нескольких переменных. Один из них см стр……..

Методы касательных. Здесь расчет нелинейной функции заменяются приближенным расчетом линейных функций. Возьмем функцию

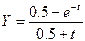
Её производная

1-ый шаг – определить тот интервал (а, в), где находится extr. Надо знать, что у нас max или min. Пусть в нашем примере (0, 0.2).

2-ый шаг – Записывают уравнение касательных в точках а и в.

В точке а а =0

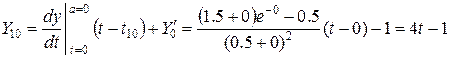
В точке в в =2.5

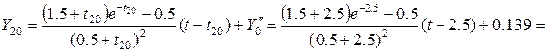
3-ый шаг – Находим точку пересечения этих касательных т.е. .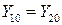

В этой точке вычисляем значения функции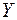

4-ый шаг – В этой точке составляем уравнение касательной предварительно скажем, что предыдущие шаги (их суть) в том, чтобы Функцию аппроксимировать каким то многоугольником, составленных из касательных. Это (из чертежа видно) – грубая аппроксимация, на 4 шаге мы уточняем эту аппроксимацию.

5-ый шаг – т.к. кривая уже аппроксимирована 3-мя касательными – многоугольником.

Найдем точку пересечения этой касательной Y₃₀ c касательными Y₁₀ и Y₂₀. В этих точках вычисляем значения функции «Y». Т.к. мы ищем max Y, то из этих 2-ух точек берем точку, для которой Y больше.

1. Метод Ньютона

2. Метод Секущих

3. Метод Хорд

4. Метод дихотомии

5. Метод Фибоначчи

6. Метод золотого сечения

7. Метод деления отрезка пополам

8. Метод квадратичной интерполяции

9. Метод кубической интерполяции

Дата добавления: 2014-01-11