КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы, связанные с градиентом
|
|
|
|
1шаг. Определяем, принадлежит ли точка абсолютного 
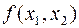 многоугольника ограничений. Если да, то задача решена; если нет то
многоугольника ограничений. Если да, то задача решена; если нет то  будет на границе многоугольника ограничений.
будет на границе многоугольника ограничений.
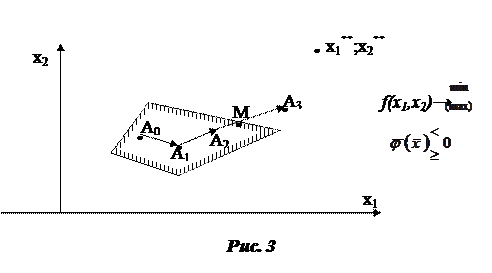
Берется внутри многоугольника любая начальная точка и из этой точки организуется движение к точке 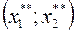 любым известным методом (координатного спуска, метод наискорейшего спуска и т.д.). Это движение происходит по итерациям. На каждой итерации проводится проверка на принадлежность полученной точки многоугольнику ограничений, затем делают следующий шаг – опять проверка и т.д. Если в результате новой итерации полученная точка не принадлежит уже многоугольнику, то тем самым мы определяем какую грань (ребро) мы «пронзили».
любым известным методом (координатного спуска, метод наискорейшего спуска и т.д.). Это движение происходит по итерациям. На каждой итерации проводится проверка на принадлежность полученной точки многоугольнику ограничений, затем делают следующий шаг – опять проверка и т.д. Если в результате новой итерации полученная точка не принадлежит уже многоугольнику, то тем самым мы определяем какую грань (ребро) мы «пронзили».
Применяя метод Лагранжа, можно найти на этом ребре точку  (но это не всегда так). Поэтому можно поступить иначе. Найдя точку
(но это не всегда так). Поэтому можно поступить иначе. Найдя точку 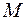 , из нее организуем движение по этому ребру, приближаясь к
, из нее организуем движение по этому ребру, приближаясь к  , опять допустим градиентным методом или используя идеи метода Лагранжа.
, опять допустим градиентным методом или используя идеи метода Лагранжа.
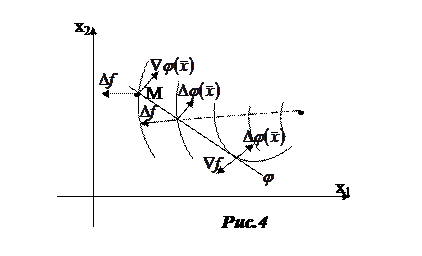
По Лагранжу 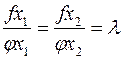 .
.
В экстремум точки 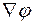 и
и 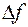 должны быть на одной линии. В точке
должны быть на одной линии. В точке 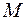 они не на одной линии. Делаем из точки
они не на одной линии. Делаем из точки 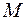 пробные шаги в обе стороны и смотрим, усилилось ли или ослабло неравенство:
пробные шаги в обе стороны и смотрим, усилилось ли или ослабло неравенство:
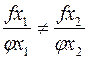 .
.
И в нужном направлении двигаемся до тех пор, пока 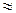
 два градиента будут лежать на одной линии. Это 1-ая модификация обхода с помощью соотношения градиентов. Есть и другая модификация:
два градиента будут лежать на одной линии. Это 1-ая модификация обхода с помощью соотношения градиентов. Есть и другая модификация:
2) Спроектируем на грань градиент . В
. В  точке
точке  .
.
Если мы ищем «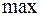 », то
», то  указывает нужное направление, если ищем «
указывает нужное направление, если ищем « », то
», то  указывает другое направление. В нужном направлении двигаемся до тех пор, пока
указывает другое направление. В нужном направлении двигаемся до тех пор, пока  не станет равен 0.
не станет равен 0.
|

Здесь был рассмотрен случай, когда ограничения линейные. Этот метод работает и в общем случае, т.е., когда ограничения нелинейные. Вообще говоря, это метод применим и для не выпуклых функций т.е. для общей задачи нелинейного программирования. Какие недостатки у этого метода? Прохождение вершин. Попадая в вершину, мы затрудняемся сказать, по какой грани дальше двигаться, особенно в многомерном случае.
|
|
|
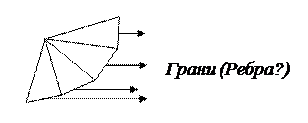
Однако есть способы, позволяющие избежать прохождение вершин. Для этого можно исследовать движение из начальной точки внутри многоугольника методом наискорейшего спуска 3-м способом, т.е. при  , тогда движение будет
, тогда движение будет 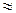 по градиенту и мы проткнем грань многоугольника в районе
по градиенту и мы проткнем грань многоугольника в районе  .
.
Пример. (рис. **)





1 шаг. Находим точку абсолютного 

Проверяем, принадлежит ли она нашему многоугольнику. Опускаем вычисления – не принадлежит.
2 шаг Выбираем начальную точку и организуем движение к  .
.

Из этой точки любым известным методом организуем движение к точке абсолютного  .
.
Воспользуемся, например, метод наискорейшего спуска.
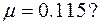


Проверим принадлежность этой точки многоугольнику ограничений.
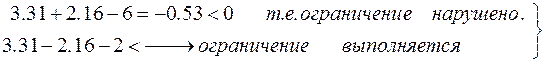 !
!
Следовательно, линия градиента пересекает 1ребро, а 2-ое не пересекает. Т.е. проходит через 1ребро, а не через пересечение 1-го и 2-го ребра.
3 шаг. Найдем точку пересечения направления градиента с ребром. Составим уравнение прямой, проходящей через две точки 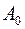 и
и 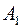 .
.
 в числах имеем:
в числах имеем:
 .
.
У нас есть уравнение  , т.к. ребро поэтому строгое равенство.
, т.к. ребро поэтому строгое равенство.
Решение:

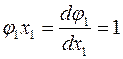
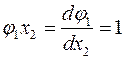
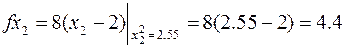
Отсюда координаты точки пересечения
 тока
тока 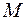
Является ли эта точка решением задачи? Т.е. касается ли сечение уровня в этой точке ребра  ?
?
4 шаг. Это выявим на 4 шаге. Если нет, то необходимо организовать движение по ребру.
Проверим это
 должно быть, если это решение задачи.
должно быть, если это решение задачи.

Тогда  т.е. точка
т.е. точка  не является решением задачи. Куда двигаться –вверх или вниз от точки пересечения? Сделаем пробные шаги в обоих направлениях.
не является решением задачи. Куда двигаться –вверх или вниз от точки пересечения? Сделаем пробные шаги в обоих направлениях.

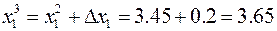


Неравенство усилилось, следовательно это направление движения по ребру неправильное.
|
|
|
Тогда возьмем 

Видно, что шаг слишком большой т.к. было  , а стало
, а стало 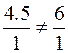
Возьмем 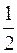 шага
шага 
Ещё итерация 

т.е. точка (3.4;2.6) является решением задачи.
Таким образом для приведенной задачи большая трудоемкость.
Возьмем тот же рисунок, но начальную точку выберем другую  то же внутри многоугольника ограничений.
то же внутри многоугольника ограничений.
Методом наискорейшего спуска делаем 1-ый шаг и получаем точку  ;
; 
Двигаемся по ребру, но по ребру то 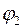 , а мы уже знаем, что решение на ребре 1. Поэтому мы должны перейти вершину. Это большая неприятность, ибо в многомерном случае – по какой грани двигаться дальше? (В плоскости ясно – там в вершине 2 ребра, значит надо двигаться по другому). В принципе в вершине можно определить углы между вектором градиента и всеми гранями и двигаться туда (по той грани) где угол наименьший (т.е. проекция градиента и антиградиента – наибольший). Это весьма трудоемкое дело. Значит надо избегать обхода вершин. Это можно сделать, если использовать метод наискорейшего спуска с постоянным шагом по одной координате. Тогда мы пресечем ту грань, которую надо, т.е. на которой лежит
, а мы уже знаем, что решение на ребре 1. Поэтому мы должны перейти вершину. Это большая неприятность, ибо в многомерном случае – по какой грани двигаться дальше? (В плоскости ясно – там в вершине 2 ребра, значит надо двигаться по другому). В принципе в вершине можно определить углы между вектором градиента и всеми гранями и двигаться туда (по той грани) где угол наименьший (т.е. проекция градиента и антиградиента – наибольший). Это весьма трудоемкое дело. Значит надо избегать обхода вершин. Это можно сделать, если использовать метод наискорейшего спуска с постоянным шагом по одной координате. Тогда мы пресечем ту грань, которую надо, т.е. на которой лежит  .
.
Приведем решение этой задачи этим методом. Не надо забывать, что здесь после каждого шага надо проверять, не вышли ли мы за многоугольник ограничений?
Итак: 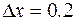
 Поэтому в сложных случаях можно начинать решение прямо с это го метода, тогда почти всегда гарантируется непопадание в вершины. Однако объем движений существенно возрастает.
Поэтому в сложных случаях можно начинать решение прямо с это го метода, тогда почти всегда гарантируется непопадание в вершины. Однако объем движений существенно возрастает.
Движение по ограничению можно ограничивать не по Лагранжу, как мы сейчас делали, а по проекциям градиента.

В любой точке  записывается уравнение касательной к
записывается уравнение касательной к  и нормальной к
и нормальной к  и проектируется эта нормальна на касательной.
и проектируется эта нормальна на касательной.
Уравнение нормали в многомерном случае в точке 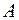
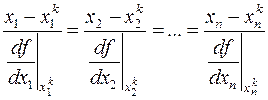
Уравнение касательной к  в точке
в точке 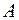 .
.

В  точке нормаль
точке нормаль  к касательной, т.е. скалярной произведение нормали и касательной должно быть =0.
к касательной, т.е. скалярной произведение нормали и касательной должно быть =0.
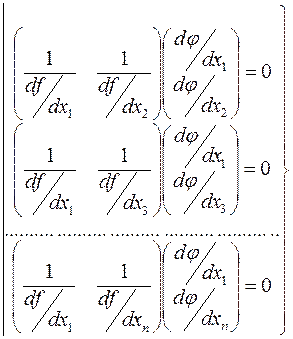
Пример.
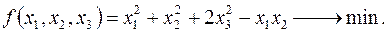
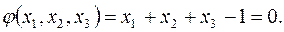
Эту задачу можно решить методом Лагранжа, но мы решим градиентом для практики.
Зададим начальную точку.
Запишем уравнение нормали:


Это 2 плоскости, пересечение которых и дает линию градиента.
1-ая плоскость
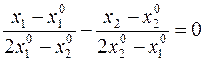 или после преобразований
или после преобразований
 ; где
; где
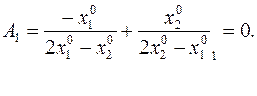
Уравнение второй плоскости

Пересечение этих двух плоскостей и дает нормаль к  . Запишем уравнение касательной. В нашем случае уравнение касательной и есть наше ограничение т.е.
. Запишем уравнение касательной. В нашем случае уравнение касательной и есть наше ограничение т.е.  =0. Для неё
=0. Для неё
|
|
|

Запишем условие экстремальности, т.е. =0 скалярного произведения.
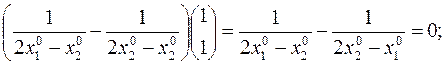
Отсюда 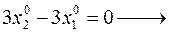 1-ое условие
1-ое условие  для начальной точки
для начальной точки  т.е.
т.е.  для произвольно выбранной точки
для произвольно выбранной точки  (если он имеет место).
(если он имеет место).
Второе условие:
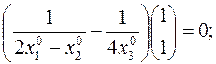 имеем
имеем  (2)
(2)
Зададим начальную точку 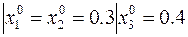
Из  получаем при заданном
получаем при заданном 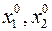 координату
координату 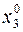 .
.
Подставим их в 1-ое и 2-ое условие и увидим, что она не является  точкой. Как же нам двигаться по плоскости
точкой. Как же нам двигаться по плоскости  чтобы попасть в
чтобы попасть в  ? Возьмем
? Возьмем 
Неравенство (2) только усилилось, следовательно, шагнули не в ту сторону. Попробуем взять точку ниже:
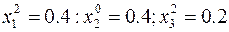
 . Неравенство стало ближе к равенству, следовательно, в этом направлении и необходимо двигаться дальше.
. Неравенство стало ближе к равенству, следовательно, в этом направлении и необходимо двигаться дальше.

 перескочили
перескочили  точки. Так, постепенно мы подойдем к
точки. Так, постепенно мы подойдем к  точке.
точке.
Литература
1. Д. Химмельблау. Прикладное программирование. М.:, Мир, 1975.
2. Лященко И.Н. и др. Линейное и нелинейное программирование. В.шк., Киев, 1975.
3. Монахов В.М. и др. Методы оптимизации М.: Просвещение, 1978.
Глава II
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 261; Нарушение авторских прав?; Мы поможем в написании вашей работы!