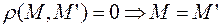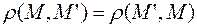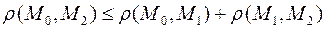КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие об эмпирических формулах
Основные разложения
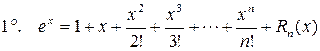 .
.
 .
.
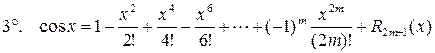 .
.
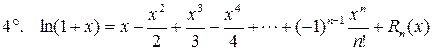 .
.
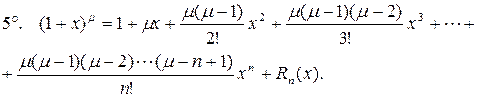
В частности, при 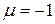
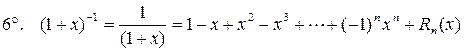 .
.
 .
.
Используя основные разложения можно получать формулы Тейлора для других функций. При этом используют то, что
 ;
;
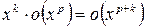 ;
;
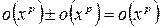 ;
;
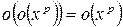 ;
;
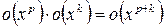 ;
;
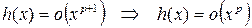 .
.
На практике часто возникает задача аппроксимации данных о зависимости между двумя переменными  и
и 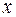 , полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функции
, полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функции 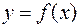 так, чтобы эта формула наилучшим образом отражала общую тенденцию зависимости
так, чтобы эта формула наилучшим образом отражала общую тенденцию зависимости  от
от 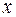 , исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.
, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.
Формулы, служащие для аналитического представления опытных данных, называются эмпирическими. Задача нахождения эмпирических формул выполняется в два этапа:
ü Установление вида зависимости 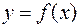
ü Определение неизвестных параметров этой функции
При определении вида эмпирической функции 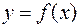 обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).
обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).
Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов в качестве неизвестных параметров функции 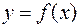 выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений
выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений 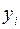 от значений функции
от значений функции 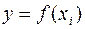 вычисленных по соответствующим им значениям аргументов
вычисленных по соответствующим им значениям аргументов 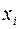 , т.е.
, т.е.
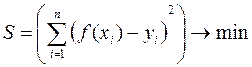
Разность 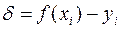 называется невязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.
называется невязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.
В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции 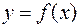 возникает необходимость поиска экстремума функции нескольких переменных, поэтому прежде чем решать эту задачу для конкретных эмпирический функций необходимо рассмотреть свойства функций нескольких переменных.
возникает необходимость поиска экстремума функции нескольких переменных, поэтому прежде чем решать эту задачу для конкретных эмпирический функций необходимо рассмотреть свойства функций нескольких переменных.
Контрольные вопросы к теме
1. Критерии монотонности функции.
2. Необходимое и достаточное условия существования экстремума функции.
3. Понятие стационарных точек функции.
4. Области выпуклости графика функции и точки перегиба.
5. План исследования функции и построение ее графика.
6. Интерполяция и аппроксимация функций.
7. Интерполяционный полином Лагранжа.
8. Формула Тейлора и формула Маклорена.
9. Понятие эмпирических функций.
Тема 4. Пространство  .
.
Основные понятия, включенные в систему тренинг-тестирования:
точка; расстояние; сфера; точка сгущения; внутренняя точка; внешняя точка; граничная точка; изолированная точка; открытая область; замкнутое множество; совершенное множество; сходимость последовательности точек; ограниченная последовательность точек; функция нескольких переменных; непрерывность функции; дифференцируемость функции; частные приращения; частные производные; композиция функций; полный дифференциал функции; формула Тейлора; локальный экстремум; стационарные точки; критические точки; условный экстремум; метод наименьших квадратов.
4.1 Точки, расстояние. Множества в  .
.
Последовательное 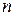 –кратное выполнение операции декартова произведения множества действительных чисел
–кратное выполнение операции декартова произведения множества действительных чисел 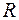 на само себя формирует множество
на само себя формирует множество  элементов, представляющих собой упорядоченные наборы
элементов, представляющих собой упорядоченные наборы 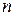 чисел
чисел 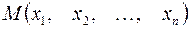 . Такие наборы называют точками. Множество всех таких точек образует
. Такие наборы называют точками. Множество всех таких точек образует 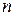 -мерное арифметическое пространство
-мерное арифметическое пространство  . При
. При  получаем арифметическое пространство
получаем арифметическое пространство  или плоскость. При
или плоскость. При 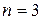 ‑ арифметическое пространство
‑ арифметическое пространство  или обычное 3-х мерное пространство.
или обычное 3-х мерное пространство.
Точки можно складывать и умножать на число.
Так, если  а
а 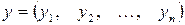 , то:
, то:
 ,
,
 .
.
Расстоянием между точками 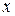 и
и 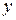 принято называть число
принято называть число
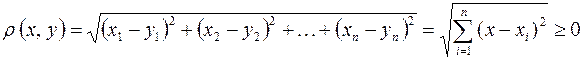 При
При  и
и 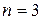 ‑ это обычное расстояние между точками на плоскости или в пространстве.
‑ это обычное расстояние между точками на плоскости или в пространстве.
Расстояние обладает следующими свойствами:
С помощью понятия расстояния 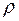 можно определить понятие сферы радиуса
можно определить понятие сферы радиуса 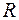 с центром в точке
с центром в точке  , как множество точек, каждая из которых находится на расстоянии
, как множество точек, каждая из которых находится на расстоянии 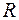 от точки
от точки  .
.
Шаром с радиусом 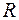 и центром в точке
и центром в точке  называется множество точек
называется множество точек  удаленных от точки
удаленных от точки  на расстояние не превосходящее
на расстояние не превосходящее 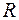 :
:
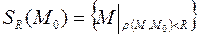
Множество 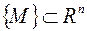 называется ограниченным, если оно целиком содержится в некотором шаре. Нетрудно показать, что ограниченность множества
называется ограниченным, если оно целиком содержится в некотором шаре. Нетрудно показать, что ограниченность множества 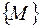 означает, что существует такое число
означает, что существует такое число 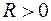 , что величины координат любой точки
, что величины координат любой точки 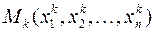 из
из 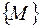 по абсолютной величине не превосходит
по абсолютной величине не превосходит 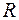 .
.
Пусть число 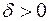 сколь угодно мало, тогда множество точек
сколь угодно мало, тогда множество точек 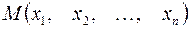 , координаты которых удовлетворяют неравенству
, координаты которых удовлетворяют неравенству
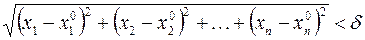
называются 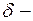 окрестностью точки
окрестностью точки 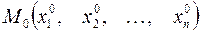 , т.е. для всех точек
, т.е. для всех точек 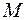 из
из 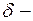 окрестности точки
окрестности точки  расстояние
расстояние 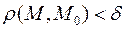 .
.
Далее, используя понятие 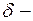 окрестности, можно ввести классификацию точек области
окрестности, можно ввести классификацию точек области 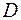 .
.
Точка  называется предельной или точкой сгущения области
называется предельной или точкой сгущения области 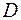 , если в любой
, если в любой 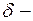 окрестности точки
окрестности точки  найдутся точки множества
найдутся точки множества 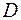 , отличные от точки
, отличные от точки  .
.
Точка  называется внутренней точкой множества
называется внутренней точкой множества 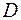 , если она входит в
, если она входит в 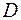 вместе с некоторой окрестностью. Любая внутренняя точка является предельной точкой множества, однако обратное утверждение не верно. Например, множество рациональных чисел
вместе с некоторой окрестностью. Любая внутренняя точка является предельной точкой множества, однако обратное утверждение не верно. Например, множество рациональных чисел 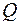 составлено только из предельных точек, но ни одна из них не является внутренней точкой.
составлено только из предельных точек, но ни одна из них не является внутренней точкой.
Точка  называется внешней точкой множества
называется внешней точкой множества 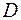 , если в
, если в 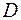 не входит ни сама точка
не входит ни сама точка  ни точки ее
ни точки ее 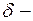 окрестности.
окрестности.
Точка  называется граничной точкой множества
называется граничной точкой множества 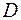 , если любая ее
, если любая ее 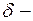 окрестность содержит как точки принадлежащие множеству
окрестность содержит как точки принадлежащие множеству 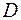 , так и не принадлежащие ему.
, так и не принадлежащие ему.

Точка  называется изолированной точкой множества
называется изолированной точкой множества 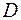 , если она принадлежит
, если она принадлежит 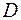 , но имеет некоторую окрестность, в которой отсутствуют точки этого множества, отличные от
, но имеет некоторую окрестность, в которой отсутствуют точки этого множества, отличные от  . Изолированными точками являются, например, целые числа.
. Изолированными точками являются, например, целые числа.
Множество, составленное из одних внутренних точек, называется открытой областью. Множество, которое содержит все свои предельные точки, называется замкнутым. Множество, которое не содержит изолированных точек, называется совершенным.
Выполнение простейших операций над множествами, таких как объединение и пересечение, позволяет сформулировать следующие общие свойства множеств:
- Любое объединение бесконечного числа открытых множеств
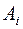 является открытым множеством
является открытым множеством - Любое пересечение бесконечного числа замкнутых множеств
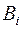 является замкнутым множеством
является замкнутым множеством - Всякое конечное объединение замкнутых множеств является замкнутым множеством
- Всякое конечное пересечение открытых множеств является открытым множеством
Примечания:
- Бесконечное объединение замкнутых множеств может оказаться незамкнутым множеством
- Бесконечное пересечение открытых множеств может оказаться неоткрытым множеством
4.2 Последовательности в 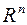 . Сходимость.
. Сходимость.
Аналогично последовательности чисел, можно определить последовательность точек 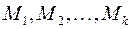 . Рассмотрим последовательность точек пространства
. Рассмотрим последовательность точек пространства 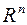 :
:

Говорят, что эта последовательность сходится к точке  , если величина расстояния между точками
, если величина расстояния между точками  и
и  есть величина бесконечно малая и с ростом
есть величина бесконечно малая и с ростом 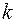 стремится к нулю:
стремится к нулю:

Можно дать и другое определение сходящейся последовательности.
Пусть  – последовательность точек в
– последовательность точек в 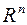 . Эта последовательность сходится к точке
. Эта последовательность сходится к точке  , если последовательность
, если последовательность 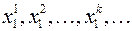 сходится к
сходится к  , т.е.
, т.е.  ; последовательность
; последовательность  сходится к
сходится к 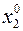 , т.е.
, т.е. 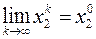 и т.д.
и т.д.
Так же, как и в случае числовой последовательности, любая 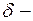 окрестность точки сгущения последовательности точек
окрестность точки сгущения последовательности точек 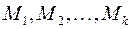 в
в 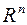 содержит бесконечное число элементов последовательности.
содержит бесконечное число элементов последовательности.
Понятие последовательности точек 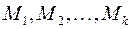 в
в 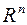 предполагает наличие биективного отображения между элементами множества
предполагает наличие биективного отображения между элементами множества 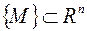 и множеством натуральных чисел
и множеством натуральных чисел  . Если выделить последовательность
. Если выделить последовательность  из множества
из множества  , то соответствующие элементы
, то соответствующие элементы  образуют подпоследовательность последовательности
образуют подпоследовательность последовательности 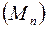 . Другими словами, подпоследовательность – это любая бесконечная часть последовательности.
. Другими словами, подпоследовательность – это любая бесконечная часть последовательности.
Всякая ограниченная последовательность точек в пространстве 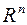 содержит подпоследовательность, сходящуюся к некоторой точке из
содержит подпоследовательность, сходящуюся к некоторой точке из 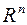 . Таким образом, если последовательность точек
. Таким образом, если последовательность точек 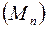 ограничена, т.е. заключена внутри некоторого шара, то ввиду бесконечности этой последовательности, внутри этого шара обязательно должны найтись места сгущения этой последовательности (должны существовать подпоследовательности, сходящиеся к некоторым внутренним или граничным точкам этого шара).
ограничена, т.е. заключена внутри некоторого шара, то ввиду бесконечности этой последовательности, внутри этого шара обязательно должны найтись места сгущения этой последовательности (должны существовать подпоследовательности, сходящиеся к некоторым внутренним или граничным точкам этого шара).
4.3 Функции в 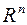 . Предел. Теорема Гейне.
. Предел. Теорема Гейне.
Если 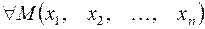 из области
из области 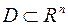 по определенному правилу или закону ставится в соответствие единственное значение величины
по определенному правилу или закону ставится в соответствие единственное значение величины 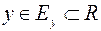 , то говорят, что на области
, то говорят, что на области 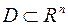 определена функция
определена функция  . Координаты
. Координаты 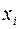 точки
точки 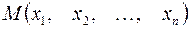 называются независимыми переменными или аргументами функции, переменная
называются независимыми переменными или аргументами функции, переменная  зависимой переменной, а символ
зависимой переменной, а символ 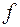 обозначает закон соответствия.
обозначает закон соответствия.
Описание законов соответствия  в многомерном случае имеют намного более ограниченные возможности, нежели в одномерном случае. К основным способам задания функции нескольких переменных можно отнести:
в многомерном случае имеют намного более ограниченные возможности, нежели в одномерном случае. К основным способам задания функции нескольких переменных можно отнести:
1. Формульный или аналитический
2. Структурно-логический
3. Геометрический
Геометрический способ задания функции затруднен уже при 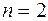 , поскольку в этом случае график функциональной зависимости совпадает с поверхностью вида
, поскольку в этом случае график функциональной зависимости совпадает с поверхностью вида 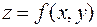 , построенной в трехмерном пространстве.
, построенной в трехмерном пространстве.
Для того чтобы лучше представить себе характер изменения графика при различных значениях аргументов 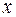 и
и  в пространстве, задают плоские сечения поверхности плоскостями, соответствующими фиксированным значениям функции
в пространстве, задают плоские сечения поверхности плоскостями, соответствующими фиксированным значениям функции 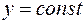 . Получающиеся в каждом сечении кривые называют линиями уровня.
. Получающиеся в каждом сечении кривые называют линиями уровня.
Уже при 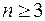 наглядность в задании функциональной зависимости исчезает и все представления такого рода относятся к рассмотрению гиперповерхностных форм.
наглядность в задании функциональной зависимости исчезает и все представления такого рода относятся к рассмотрению гиперповерхностных форм.
Определение предела функции по Коши:
Пусть дана функция  , определенная на области
, определенная на области 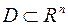 . Число
. Число 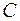 называется пределом
называется пределом  в точке сгущения
в точке сгущения  если
если 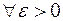
 такое, что
такое, что 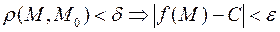 .
.
Символически обозначение предела выглядит следующим образом:
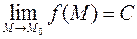
Определение предела функции по Гейне:
При любом выборе последовательности точек 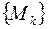 , сходящейся к точке сгущения
, сходящейся к точке сгущения 
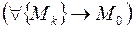 соответствующие числовые последовательности значений функции
соответствующие числовые последовательности значений функции 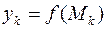 сходятся, причем у всех последовательностей
сходятся, причем у всех последовательностей 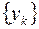 должен быть единый предел.
должен быть единый предел.
4.4 Непрерывность функции в 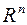 .
.
Рассмотрим функцию  , определенную в области
, определенную в области 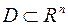 . Предположим, что лишь одна переменная
. Предположим, что лишь одна переменная 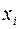 получила приращение
получила приращение 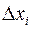 , а остальные переменные остались неизменными. Тогда разность
, а остальные переменные остались неизменными. Тогда разность
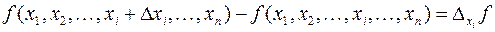
называется частным приращением функции  по переменной
по переменной 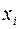 .
.
Функция  называется непрерывной по переменной
называется непрерывной по переменной 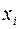 , если функция определена как в точке
, если функция определена как в точке 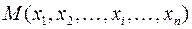 , так и в точке
, так и в точке 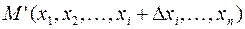 , и эти точки являются точками сгущения этой функции. При этом должно выполняться условие
, и эти точки являются точками сгущения этой функции. При этом должно выполняться условие 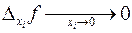 , т.е. бесконечно малым приращениям переменной
, т.е. бесконечно малым приращениям переменной 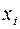 должны соответствовать бесконечно малые частные приращения функции
должны соответствовать бесконечно малые частные приращения функции  .
.
Если приращение получают все переменные, то соответствующее приращение функции 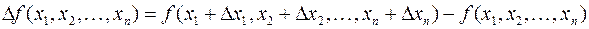
называется полным приращением функции (или просто приращением функции).
Естественно, что во всех точках, соответствующих как частным приращениям, так и полному приращению функции, сама функция должна быть определена.
Также следует отметить, что полное приращение функции, вообще говоря, не равно сумме частных приращений:
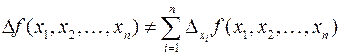
Функция многих переменных, определенная в 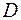 , называется непрерывной в точке сгущения
, называется непрерывной в точке сгущения  , если:
, если:
1. 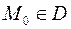
2. 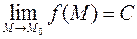
3. 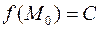
Из данного определения следует, что
1. функция должна быть определена в точке  и эта точка должна быть предельной в области существования функции
и эта точка должна быть предельной в области существования функции
2. приращение 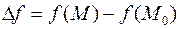 для любой непрерывной функции является величиной бесконечно малой:
для любой непрерывной функции является величиной бесконечно малой:  причем это условие должно выполняться и для всех частных приращений функции
причем это условие должно выполняться и для всех частных приращений функции 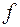
Таким образом, для выполнения требования непрерывности функции нескольких переменных в точке необходимо, чтобы функция была непрерывна как в самой точке, так и в некоторой окрестности этой точки, причем при достаточно малых по абсолютной величине приращениях переменных 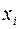
|
|
Дата добавления: 2014-01-13; Просмотров: 1072; Нарушение авторских прав?; Мы поможем в написании вашей работы!