Типы конечных автоматов

В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Однако такое понимание яв­ляется слишком узким. В широком смысле конечный автомат - это мате­матическая модель, отображающая фи­зические или абстрактные явления самой разнообразной природы. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различ­ные объекты, устанавливать связи и аналогии между ними, пере­носить результаты из одной области в другую.

Конечный автомат М определяется как система с конечным вход­ным алфавитом 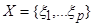, конечным выходным алфави­том 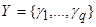, конечным множеством состояний 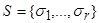и двумя характеристическими функциями:

;

,

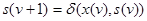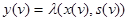называемыми соответственно функцией переходов и функцией выходов.

Рис.11.1. Блок-схема конечного автомата

Общая блок-схема конечного автомата (рис. 11.1) может быть пред­ставлена в виде комбинационной схемы, реализующей характерис­тические функции d и l, и памяти, сохраняющей на один такт пре­дыдущее состояние автомата.

В определении автомата участвует три конечных множества X, Y, S и две функции d и l, задающие некоторые отношения между элементами этих множеств. Следовательно, конечный автомат мож­но обозначить упорядоченной пятеркой М = (X, Y, S, d, l). Мощ­ности множеств X, Y, S равны соответственно:

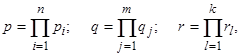
где 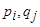и 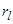- количество символов в алфавитах входной пере­менной X_i, выходной переменной 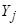и переменной состояния 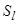. При двоичном структурном алфавите , 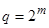и 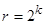. Если желают подчеркнуть мощности множеств X, Y и S, на которых определен конечный автомат, то его называют (р, q, r)- автоматом.

Характеристические функции d и l можно рассматривать как некоторые отображения множества 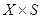или его подмножества 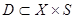соответственно на множества S и Y. Если 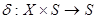и , автомат называется полным; если только 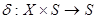, автомат называется полным по переходам. В случае, когда функции d и l определены не для всех наборов из множества 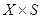, автомат называют неполным или частично опре­деленным.

Приведенное выше определение связывают обычно с автоматом первого рода, называемым также автоматом Мили. Если выходные переменные являются функцией только состояния, то имеем автомат второго рода или автомат Мура.

Между автоматами этих двух типов имеется взаимная связь и один из них может быть преобразован в другой.

Дата добавления: 2014-01-13