Властивості множини цілих чисел

Розглянемо спочатку деякі властивості побудованої вище мно­жини М.

Можна довести такі твердження:

1. Для довільних цілочисельних точок К і L виконується одне і тільки одне з трьох співвідношень: точки К і b збігаються; точка К лежить зліва від точки L; точка L лежить зліва від точки К.

2. Відношення «лежить зліва від» на множині М є транзитивним і
aсиметричним. Відношення «лежить зліва від» позначається симво­
лом -<.

Теорема 1, Система (М, –<) є лінійно упорядкованою множи­
ною.

Теорема 2. Множина М еквівалентна множині Z

Однією з властивостей множини N є її впорядкованість. Покажемо, що таку саму властивість має і множина Z.

Означення 4...Говорять,,що ціле число к дорівнює цілому числу ℓ, і записують к =ℓ, якщо к і ℓ — позначення одного і того самого ці­
лого числа.

Таким чином, умова к=ℓ, Де к, ℓ Є Z, рівносильна тому, що точки К і L, які є зображеннями; на числовій прямій відповідно чисел к і ℓ, збігаються.

Означення 5, Нехай к і ℓ — два різні цілі числа, а відповідно точки К і L — їх зображення на числовій прямій. Говорять, що число к менше від числа ℓ, або число ℓ більше за число к, і записують відповід­но к < ℓ, або ℓ> к, якщо точка К лежить зліва від точки L.

Те о р е м а 3. Для довільних цілих чисел к і l виконується одне і тільки одне з трьох співвідношень: к =ℓ, к <ℓ x, ℓ < к.

Теорема 4. (транзитивність)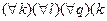< l 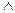l < q), k, l, q Є Z.

Доведення. За означенням 5 k < l ↔ K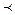L i l < q ↔ L 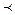Q, де К, L, Q – точки, які є зображенням на числовій прямій відповідно чисел k, l, i q. Тому k < l 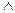l < q→K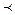Q → k < q.

Теорема 5. (асиметричність)

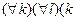< l l < k), k,l Є Z

Доведення. Нехай k < l. Припустимо, що l < k. Тоді за попередньою теоремою k < k. Зайшли у суперечність.

Теорема 6. Система (Z, <) – лінійновпорядкована множина.

Розглянуті вище властивості множини Z цілих цілих чисел дають змогу записати цю множину у вигляді "двостороннього ряду"

…, - n, …, - 2, -1, 0, 1, 2, …, n, …,

який показує, що множина Z не обмежена (як зверху, так і знизу) і дискретна.

Дата добавления: 2014-01-13