Изображение физических величин операторами

Разложение по собственным функциям непрерывного спектра

Произвольную функцию ψ (х) можно представить в виде

где что вытекает из условия нормировки.

В квантовой механике физические величины изображаются линейными эрмитовыми операторами. Такое ограничение на класс операторов вытекает из требования вещественности физических величин.

а) координаты :

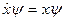или (20)

Собственная функция оператора х, соответствующая собственному значению а, удовлетворяет равенству

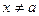Так как х – переменная величина, а – произвольная фиксированная, то равенство справедливо только в том случае, если при т.е.

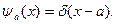
И для оператора радиус-вектора частицы 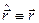имеем

б) импульса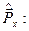

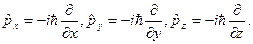(21)

И в общем случае

(22)

где - оператор «набла».

.

Здесь - единичные векторы, направленные по осям координат

Cобственные значения оператора импульса можно найти из уравнения

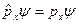или (23)

Найдем собственные функции оператора импульса для одномерного движения, т.е. для 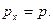Решением уравнения (23) является выражение

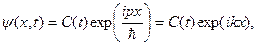(24)

где k – волновое число, (в обычной механике) или C (t) - некоторая функция времени. Общее решение нестационарного уравнения Шредингера имеет вид

Сравнивая это выражение с уравнением (24), видим, что

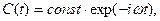
где ω – частота волны де Бройля. Тогда получаем

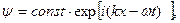
т.е. собственными функциями оператора импульса являются плоские волны де Бройля. Спектр собственных значений оператора импульса является непрерывным, так как вероятность обнаружить какое-либо значение импульса является постоянной величиной, не зависящей ни от времени, ни от координат. Для доказательства этого рассчитаем среднее значение проекции импульса:

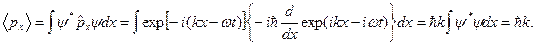
в) кинетической энергии:

. (25)

Его собственные функции совпадают собственными функциями оператора импульса (они коммутируют):

Собственные функции 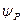находятся из уравнений для них:

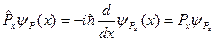
откуда

Нормированные функции для трехмерного случая

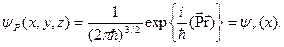
Собственные значения оператора кинетической энергии:

г) полной энергии .

Этот оператор называютоператором Гамильтона или гамильтонианом – он определяется как сумма операторов кинетической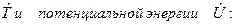

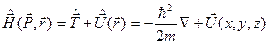(26)

д) момента импульса

поскольку момент импульса определяется как для компонент имеем выражения:

(27)

Далее рассмотрим некоторое другое представление уравнения Шрёдингера, которое понадобится для дальнейших выкладок. Квантомеханическая система определяется волновой функцией ψ, которая является решением уравнения

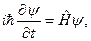(28)

где - оператор Гамильтона рассматриваемой системы. Если эта система может находиться только в дискретных состояниях ψ_α (α – набор индексов, характеризующих данное дискретное состояние), то волновую функцию системы можно разложить по полной системе ортонормированных функций {ψ_α}:

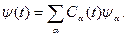
Подставим это разложение в уравнение (28):

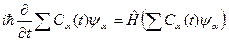(29)

Умножим соотношение (29) на и проинтегрируем по всей области изменения х:

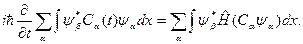
С учетом взаимной ортогональности и условий нормировки приходим к уравнению

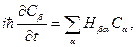(30)

где

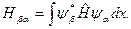
Очевидно, что Н _ββ – это энергия системы в состоянии ψ_β, а Н _βα - матричный элемент, характеризующий вероятность перехода системы из состояния 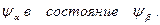Коэффициент С _α(t) представляет собой амплитуду состояния ψ _α, а | C _α|² – вероятность найти систему в состоянии ψ_α.

Дата добавления: 2014-01-11