
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема доказана
|
|
|
|
K s K
K s K
K s
K s K s
K s K s
K s K s
K s
K s
Учтем, что:
n(n+1)/2+1=(n2+n+2)/2≤(n2+2n+1)/2=(n+1)2/2 для любого n.
Тогда: nср ≤ 3log2 (n+1)+∑∑ η(n,k,s)log2 r(n,k,s) +2
Проведем некоторые тождественные преобразования.
∑∑η(n,k,s)log2 r(n,k,s)=∑∑η(n,k,s)log2 η(n,k,s)-
- ∑∑η(n,k,s)log2 pkqn-k=H′- ∑∑ η(n,k,s)k log2 p -
-∑∑η(n,k,s) (n-k) log2 q
Из комбинаторных соображений ясно (Рис. 1), что:
∑r (n,k,s)= Ckn
s
Тогда:
∑∑ η(n,k,s)k log2 p=∑ Ckn pkqn-k k log2 p ≤ n log2 p
Аналогично:
∑∑ η(n,k,s) (n-k) log2 q= ∑Ckn pkqn-k(n-k) log2 q≤ n log2 q
Следовательно:
nср ≤ 3log2 (n+1) + H′+ nH(p)+2
Rn (p) = nср /n - Н (p) ≤ (3log2 (n+1))/n+ H′/n+ Н (p)+2/n-H(p)
Так как: H′≤0
Rn (p) ≤ (3log2 (n+1))/n+2/n (8)
Следовательно: ℓim Rn = 0
n → ∞
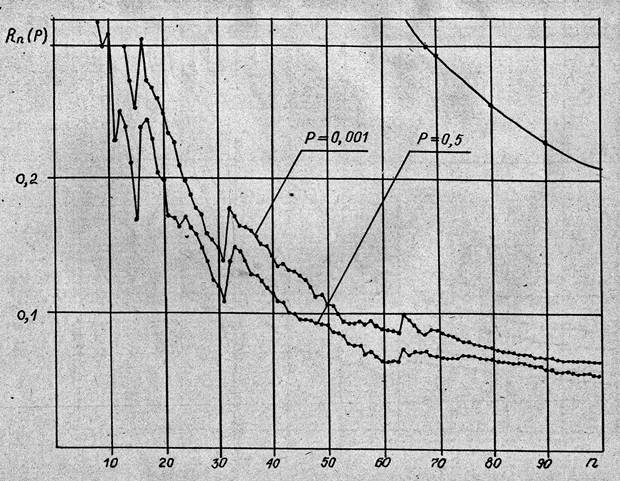
На Рис. 2 представлены графики иллюстрирующие свойства сформулированного метода кодирования. Значения избыточности кодирования были вычислены на ЭВМ в соответствии с формулами (1) и (7) с точностью до трех знаков. Показана так же верхняя граница избыточности, вычисленная по формуле (8).

Рис. 2. Зависимости избыточности кодирования
Вычисления были проведены для четырех значений вероятности появления единицы P.
Величины Р выбраны так, чтобы иметь возможность увидеть поведение избыточности кодирования для разных источников. В случае Р = 0,5 избыточность в потоке двоичных отсутствует и поэтому применение кодирования к исходной последовательности может привести лишь к увеличению объема передаваемых данных. В случае Р = 0,001 на каждые 1000 бит исходной последовательности приходится в среднем одна единица, т.е. имеет место избыточность. Вычисления показали, что если в выражение для средней длины кодового слова (7) подставить Р=0, то отличие величины избыточности от случая Р = 0,001 будет наблюдаться в четвертом знаке после запятой. Таким образом, для любого Р ≤ 0,001 величина избыточности (с точностью до трех знаков) будет совпадать с избыточностью при Р = 0,001, и в этом смысле случай Р = 0,001 наиболее «благоприятен» для применения кодирования.
|
|
|
Случаи р = 0,1 и р = 0,01 занимают промежуточное положение.
Необходимость рассмотрения этих разнообразных случаев вытекает из начального предположения об априорной неизвестности вероятности появления единиц в исходной двоичной последовательности.
Поскольку Rn(p) является дискретной функцией, определенной на множестве натуральных чисел, графики представляют собой отдельные точки, соответствующие целым n. На Рис. 2 они соединены прямыми линиями, что сделано исключительно с целью наглядности.
Видно, что для фиксированного n избыточность тем больше, чем больше отличается р от 0,5. В целом избыточность стремится к нулю с ростом n, но не монотонно и не равномерно по Р.
Из определения кодирования следует его симметричность относительно Р, т.е. кривые избыточности для Р будут совпадать с кривыми для 1-Р. Иными словами, исходная последовательность при Р=0.1 будет сжата за счет применения кодирования до такой же степени, как при Р = 0,9; при Р = 0,01 так же, как при Р =0,99 и т.д.
Вернемся к выражению для длины кодового слова (4).
L=]log 2 (n+1)[+ ]log 2 (n(n+1)/2+1 [+]log 2 r(n,k,s)[ (4).
Второе слагаемое, входящее в это выражение определяет количество разрядов необходимое для записи параметра S. Причем, это количество постоянно для данного значения n и рассчитано на максимальное значение S.
С другой стороны, для фиксированного значения k, существуют вполне определенные величины smin(k) и smax(k), вычисляемые по формулам (6).
S min(k) = k(k+1)/2;
S max(k) =kn - k(k+1)/2 (6)
Поскольку, для записи параметра k используется постоянное (для данного значения n) количество разрядов - первое слагаемое в (4), то k это первый параметр, который будет определен при декодировании (префикс). Но определив k, можно по формулам (6) вычислить соответствующие значения S, а следовательно можно заменить второе слагаемое в (4) на выражение:] log 2 (smax(k) - smin(k) + 1) [,
|
|
|
что позволит сократить длину кодового слова L.
Выражение для L будет иметь вид:
L=]log 2 (n+1)[+ ]log 2 (к(n-к)+1)[+]log 2 r(n,k,s)[ (9)
Выражение для nср так же изменится: (10)
nn smax(k)
nср =]log2 (n+1)[+ ∑Cknpkqn-k ]log 2 (к(n-к)+1)[+∑∑ η(n,k,s) ]log2 r(n,k,s)[
K=0 K=0 s=smin(k)
На Рис. 3 представлены зависимости избыточности для модифицированного метода КТ.
Сравнивая эти графики с графиками на Рис. 2 можно убедиться, что значения избыточности при фиксированном n уменьшились в разы. Кроме того, стремление Rn(p) к 0 для разных p стало более равномерным, в том смысле, что «коридор» значений Rn(p) для разных р сузился. Вычисления показали, что значения избыточности для p = 0,5; 0,1 совпадают с точностью до 3 знаков после запятой. Для p = 0,01 отличие от случая p = 0,5 меньше 0,004. Поэтому кривые при p =0,1 и 0,01 на рисунке не показаны. Для p = 0,001, начиная с n =75, это отличие не превышает 0,008.
Таким образом, модификация КТ обеспечивает не только экономию двоичных разрядов кодового слова, но и существенно более равномерное (с точностью до 3 - го знака после запятой) стремление Rn(p) к 0 для разных p. Это важно в случае неизвестной статистики при практической реализации сжатия.
Для того чтобы оценить во сколько раз снижается объем данных за счет применения модифицированного кодирования (КТ) были построены зависимости коэффициентов сжатия от n при различных p (Рис. 4).

Рис. 4. Зависимости коэффициентов сжатия от n для различных p
Коэффициенты сжатия вычислялись на ЭВМ по формуле
К сж = n/ nср (11).
Специально отметим, что такая оценка в нашем случае корректна, поскольку изначально было оговорено, что исходную последовательность двоичных данных порождает бернуллиевский источник, что полностью определяет характер избыточности при исходном разбиении на блоки. Кроме того, будем считать, что источник порождает бесконечную последовательность двоичных данных (например, если данные поступают в течение нескольких часов с частотой сотни килогерц).
На рисунках показаны так же верхняя граница для К сж, при заданном Р (1/Н(Р)) и нижняя граница, вычисляемая по формуле (11), где вместо выражения для nср используется выражение для верхней границы избыточности (8).
|
|
|
Основные выводы по графикам:
1. Значения К сж модифицированного КТ больше, чем исходного. Например, при n = 63, К сж соответственно равны: 0,94; 1,85; 6,80; 10,00 и 0,92; 1,75; 3,40; 3,60; при n = 127; 0,96; 1,95; 9,20; 18,00 и 0,94; 1,90; 5,60; 7,40.
2. Заметно, что чем ближе Р к 0,5, тем при меньших значениях n приближается к максимуму.
3. Заметны выбросы кривых в точках n = 2m – 1,
где m = 1, 2, 3,........
Отсюда, следует, что не всякое увеличение n приведет к увеличению К сж, а это важно, поскольку именно величина исходного блока в первую очередь определяет трудоемкость кодирования. В дальнейшем будет построена методика выбора n, с учетом этого факта.
Таким обрезом, если не зная ничего о величине Р применить КТ, то даже при небольших значениях n (порядка 101 - 102), можно подобрать такое n ‚ что при Р = 0,5 (наихудший для сжатия случай, когда надо просто передавать прямым кодом) потери от кодирования будут невелики (К сж ≈1), во всех других случаях будет выигрыш, тем больший, чем больше Р отличается от 0,5.
Для того, чтобы реализовать КТ, оценить его эффективность и трудоемкость, необходимо уметь вычислять значения коэффициентов r(n,k,s). В ходе анализа литературы по комбинаторике не удалось найти упоминания о коэффициентах, имеющих аналогичный смысл.
Можно отметить два наиболее близких к нашему случаю результата. Это рекуррентное соотношение для числа разбиений натурального числа на неравные слагаемые, каждое из которых меньше некоторого числа n, а так же производящая функция для такого разбиения, но при этом не накладывается ограничений на число слагаемых.
Так же, явное выражение для числа разбиений, но без ограничения на величину слагаемых.
В связи с этим сформулированы и доказаны теоремы и соотношения для вычисления коэффициентов r(n,k,s), которые являются математическим аппаратом практической реализации кодирования. Доказательства и промежуточные выражения при выводе формул в статье не приведены, в виду их громоздкости.
|
|
|
Теорема 2. Для r(n,k,s) имеет место рекуррентное соотношение:
r(n,k,s) = r(n-1,k,s)+ r(n-1,k-1,s-n) (12).
Следствие 1:
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 351; Нарушение авторских прав?; Мы поможем в написании вашей работы!