Понятие о римановой поверхности

Лекция 46.

Чтобы получить наглядное представление о взаимоотношении ветвей функции 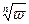, заметим, что половинам углов или 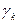соответствует в плоскости то попере­менно то верхняя, то нижняя полуплоскости. Именно, когда мы про­ходим один за другим эти полууглы в направлении против часовой стрелки, начиная с полуугла 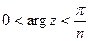, то в плоскости 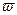полу­чаем поочерёдно сначала верхнюю полуплоскость, затем нижнюю.

Представим себе, что мы имеем по экземпляров верхних и нижних полуплоскостей, которые для наглядности будем предполагать бумажными листами неограниченных размеров. Склеивая тогда верх­нюю и нижнюю полуплоскости вдоль отрицательной полуоси (а края вдоль положительной полуоси оставляя свободными), мы получим область 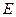Рис.44.2, соответствующую полууглам, образующим область 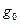.Если теперь ко второму полууглу присоединить следующий, то эти полууглы составят область 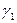, которой соответствует в плоскости 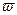область 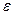, изображённая на Рис.45.2. Эта последняя образована ниж­ней и верхней полуплоскостями, соединёнными вдоль положитель­ной оси, и нам остаётся лишь приклеить к свободному краю ниж­ней полуплоскости новый экземпляр верхней полуплоскости. Получим область, образованную тремя полуплоскостями, соответственно трём полууглам плоскости 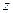. При этом две полуплоскости (верхние), соответствующие первому и третьему полууглам, будут находить­ся одна над другой. Это отвечает тому факту, что в первом и третьем полууглах функция 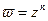принимает одни и те же значения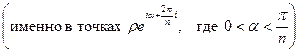

Рис.46.1.а.

Рис.46.1.б.

Отрицательная полуось третьей полуплоскости и положительная полуось первой будут оставаться свободными (Рис 46.1.а, на которой полуплоскости для наглядности деформированы). Далее, мы можем присоединить в плоскости 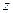четвёртый полуугол, которому должна соответствовать нижняя полуплоскость. Так как третий и четвёртый полууглы вместе образуют область , а ей отвечает область 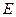Рис 44.1., состоящая из верхней и нижней, полуплоскостей, соединён­ных вдоль отрицательной полуоси, то мы должны приклеить к сво­бодной отрицательной полуоси третьей (верхней) полуплоскости новый экземпляр нижней полупло­скости. Положительная полу­ось этой последней останется свободной (Рис.46.1. б). Про­должая далее этот процесс присоединения новых полу­углов и соответствующих им полуплоскостей, мы дойдём до последнего полуугла, которому будет соответство­вать нижняя полуплоскость; её положительная полуось, так же как и положительная полуось первой (верхней) полуплоскости, остаётся свободной. Но последний и первый полууглы вместе обра­зуют область 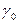(Рис.45.2. а). Соединяя эти полууглы, мы, с одной стороны, получим полную плоскость 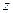, а с другой – должны будем соединить последнюю (нижнюю) и первую (верхнюю) полуплоскости вдоль положительной полуоси, благодаря чему получим замкнутую – листную поверхность, называемую римановой поверхностью функции .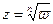

Заметим, что на нашей модели последнее склеивание не удаётся произвести фактически, гак как нижний и верхний полулисты будут разделяться 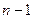лежащими между ними листами. Поэтому послед­нее склеивание нужно понимать лишь в том смысле, что мы мысленно отождествляем точки свободных положительных полуосей с одинако­выми абсциссами.

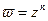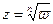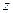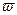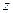Имея перед глазами риманову поверхность, легко составить себе полное представление о функции и ей обратной функции . То обстоятельство, что риманова поверхность имеет листов, соответствует тому факту, что одно и то же значение то принимается в различных точках плоскости , или, иными словами, что каждому значению соответствует различных значений (исключая точки разветвления , которым соответствует лишь по одной точке: .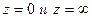

Если точка 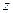, переходя из одного полуугла в другой, опишет замкнутый контур вокруг начала координат, то точка 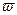, переходя из одной полуплоскости на другую и побывав, таким образом, на всех листах, опишет также замкнутый контур. Оставаясь на римановой поверхности, мы можем любую точку соединить непрерывной кри­вой с любой другой точкой . Эти две точки, в частности, могут лежать одна над другой, т. е. иметь один и тот же аффикс. 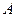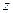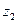Заста­вляя точку двигаться вдоль этой кривой от к , мы заставим соответствующую точку непрерывно перейти от значения , соответствующего , к значению , соответствующему т. е. мы можем непрерывным изменением перейти от одной ветви функции 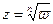к другой.

Если, наконец, мы выделим на римановой поверх­ности какую-либо область, не содержащую взаимно налегающих частей, т.е. не содержащую точек с одинаковыми аффиксами, то, оставаясь в пределах такой области, мы для каждого 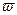будем иметь един­ственное соответствующее ему значение 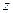, т.е. можем говорить об определённой ветви функции 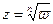(область плоскости 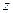, соот­ветствующая этой области римановой поверхности, будет областью однолистности функции ).

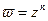Аналогичным образом можно построить римановы поверхности и для функций . Для функции 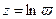построе­ние будет буквально тем же, только здесь верхние и нижние полу­плоскости будут соответствовать уже не полууглам, а полосам: 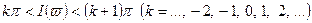, вдвое более узким, чем первоначальные. Так как среди этих полос нет ни первой, ни последней, которые могли бы граничить между собой, как граничили между собой первый и последний полууглы преды­дущего примера, то и среди полуплоскостей не будет ни первой, ни по­следней, края которых следовало бы склеивать между собой, как мы это только что делали. Риманова поверхность функции является бесконечнолистной. Также бесконечнолистной будет и риманова по­верхность функции 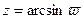; однако связь отдельных листов здесь сложнее, чем в предыдущих случаях. Когда 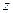меняется в области 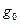(Рис.45.1.в), то, как мы видели, то описывает всю область 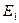. Из равенства 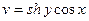следует, что знак совпадает со знаком , т.е. что заштрихованной полуполосе со­ответствует верхняя, а незаштрихованной полуполосе 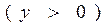— нижняя полуплоскость плоскости 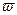. Если теперь точка 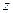будет описывать область , то точка будет описывать область 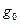и именно: верхнюю полу­полосу, когда 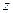описывает верхнюю полуполосу области , и нижнюю полуполосу, когда 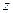описывает нижнюю полуполосу области . Но 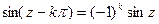. Поэтому при 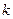, чётном верхней полуполосе области будет соответствовать, как и в случае области 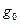верхняя полуплоскость 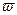, а нижней полуполосе – нижняя полуплоскость; при 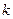, нечётном верхней полуполосе, будет соответствовать нижняя полупло­скость, а нижней полуполосе – верхняя. (На Рис.45.1. в полуполосы, которым соответствуют верхние полуплоскости плоскости 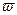, заштри­хованы.) Каждая полуполоса граничит вдоль части прямой с одной из трех полуполос и притом заштрихованная граничит с незаштрихован­ными и незаштрихованная с заштрихованными. Отсюда следует, что, присоединяя к полуполосе любую из этих соседних трех, мы получим область однолистности функции . В самом деле, внутри одной и той же полуполосы принимает разные значения в разных точках; если же одна из двух точек находится в одной, а другая в другой из двух соседних полуполос, то соответствующие точки лежат одна в верхней, а другая в нижней полуплоскости 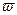, т.е. также различны.

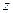Мы уже знаем область, которую описывает , когда описывает область 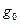(или одну из полос ). Остается лишь отметить, что парам двух соседних верхних или двух соседних нижних полуполос соответствует одна область или Рис.46.2.:

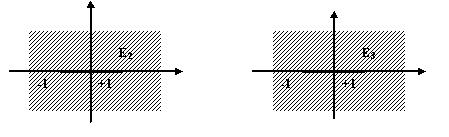
Рис.46.2.

состоит из верхней и нижней полуплоскостей, склеенных вдоль части действительной оси от +1 до +верхней и ниж­ней полуплоскостей, склеенных вдоль части действительной оси от -до -1. 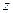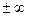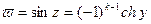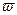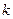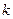В самом деле, когда точка описывает полупрямую (y, сохраняя знак, меняется от 0 до ), по которой граничат полуполосы, то точка должна описывать линию, по которой склеиваются полуплоскости , при нечетном получаем часть действительной оси от +1 до +, при четном—часть действительной оси от -до -1. Желая получить риманову поверхность функции 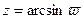, мы построим для большей наглядности сначала часть этой поверхности, соответ­ствующую верхней полуплоскости 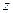, затем – нижней и, наконец, обе части соединим вместе. Начав с верхней полуполосы области 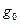, будем присоединять к ней одну за другой верхние полуполосы, лежа­щие вправо от нее; для переменного 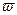мы будем получать при этом поочерёдно то верхние, то нижние полуплоскости, причем они должны скрепляться между собой то вдоль части действительной оси от +1 до +, то от -до -1.

При этом каждый раз будут оста­ваться свободными части действительных осей между -1 и +1. Кроме того, останется свободной часть от -до -1 действи­тельной оси первой (верхней) полуплоскости, соответствующая левому свободному краю верхней полу полосы 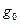. Если мы к эгому краю присоединим соседнюю левую верхнюю полуполосу, то к свободной части действительной оси первой полуплоскости придётся приклеить новую нижнюю полуплоскость. Продолжая в плоскости 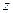присоединять одну за другой верхние полуполосы, лежащие слева от начальной, мы должны будем соответственно приклеивать к уже построенной части римановой поверхности все новые и новые полуплоскости, скре­пляя две соседние поочередно то вдоль отрезка (от -до -1), тo вдоль oотрезка (от +1 до +). В итоге получим часть римановой поверхности функции 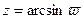, соответствующую верхней полуплоскости 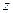, она состоит из бесконечного множества листов, среди которых нет ни первого, ни последнего. На каждом из них остаются свободными (несклеенными) два края отрезка [-1, +1]: один край принадлежит верхней, другой — нижней полуплоскости. Если мы заставим точку двигаться по этой поверхности так, чтобы ее проекция на плоскость 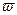описывала круг с центром в начале координат, то точка не сможет описать более половины оборота, если радиус круга меньше единицы: она остановится у несклеенных краев. В случае же, когда радиус круга будет больше единицы, точка будет описывать неограниченное мно­жество кругов, лежащих друг над другом на разных листах. При этом, отправляясь от некоторого начального положения точки и дви­гаясь, все время в одну и ту же сторону, мы побываем лишь на части листов, соответствующих верхним полуполосом, (или влево) от некоторых из них; чтобы побывать на всех остальных листах, пришлось бы, вернувшись к начальному положению, двигаться в противоположном направлении.

Рис.46.3.

Совершенно аналогичную структуру имеет часть римовой поверхности 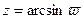, соответствующая нижней полуплоскости 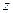(нижним полуполосам).

Чтобы получить из этих двух частей всю риманову поверхность, достаточно заметить, что, соединяя две полуполосы, верхнюю и нижнюю, в одну область , мы должны соответствующие

им полуплоскости 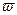соединить вдоль отрезка [-1, +1], тогда полу­чится область .

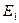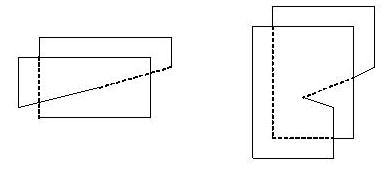
Таким образом, мы должны приклеить к каждой полуплоскости первой части римановой поверхности соот­ветствующую ей полуплоскосгь второй части вдоль остающихся сво­бодными отрезков [-1, +1]- При этом соответствующими считаются полуплоскости (верхняя и нижняя), отвечающие полуполосам одной и той же области . Заметим, что последние склеивания на модели из бумажных листов (по необходимости ограничиваясь конечным числом их) не удастся фактически провести, так как, склеив два каких-нибудь края от -1 до +1, мы создадим преграду для склеивания свободных краев, находящихся по разные стороны от заклеенного листа. На Рис.46.3.представлено схематически склеивание двух соот­ветствующих листов обеих частей римановой поверхности. (Верхняя полуплоскость верхнего листа склеена с нижней полуплоскостью ниж­него листа вдоль отрезка [— 1, 4-1]; вдоль того же отрезка склеены между собой нижняя полуплоскость верхней и верхняя полуплоскость нижней плоскости.)

Дата добавления: 2014-01-13