
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры разностных аппроксимаций
|
|
|
|
Разностные методы решения задач в частных производных
Рассмотрим равномерную разностную сетку с шагом  , т.е. множество точек
, т.е. множество точек
 .
.
Пусть 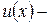 достаточно гладкая функция, заданная на отрезке
достаточно гладкая функция, заданная на отрезке 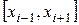 . Обозначим
. Обозначим  ,
,  ,
, 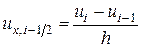 и
и  .
.
Введенные разностные отношения называются правой, левой и центральной разностными производными функции в точке  . Каждое из этих разностных отношений аппроксимирует
. Каждое из этих разностных отношений аппроксимирует 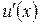 в точке
в точке  , т.е. при фиксированном
, т.е. при фиксированном  и при
и при 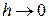 пределом этих отношений является
пределом этих отношений является  . Проводя разложение по формуле Тейлора, получим
. Проводя разложение по формуле Тейлора, получим
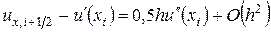 ,
,
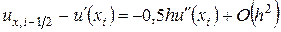 ,
,
 .
.
Отсюда видно, что левая и правая разностные производные аппроксимируют 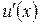 с первым порядком по
с первым порядком по  , а центральная разностная производная – со вторым порядком точности. Нетрудно показать, что вторая разностная производная
, а центральная разностная производная – со вторым порядком точности. Нетрудно показать, что вторая разностная производная
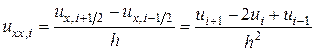
аппроксимирует 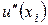 со вторым порядком аппроксимации по
со вторым порядком аппроксимации по  , причем справедливо разложение (показать)
, причем справедливо разложение (показать)
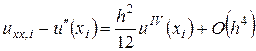 .
.
Рассмотрим дифференциальное выражение
 (1.1)
(1.1)
с переменным коэффициентом 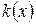 . Заменим выражение (1.1) разностным отношением
. Заменим выражение (1.1) разностным отношением
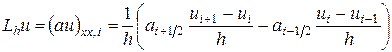 , (1.2)
, (1.2)
где 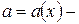 функция, определенная на сетке
функция, определенная на сетке 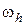 . Найдем условия, которым должна удовлетворять функция
. Найдем условия, которым должна удовлетворять функция 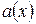 для того, чтобы соотношение
для того, чтобы соотношение 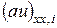 аппроксимировало
аппроксимировало 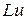 в точке
в точке  со вторым порядком аппроксимации по
со вторым порядком аппроксимации по  .
.
Подставляя в (1.2) разложения
 ,
,
 ,
,
где 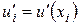 , получим
, получим
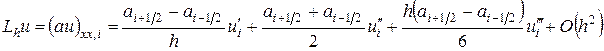 .
.
С другой стороны,
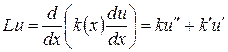 ,
,
т.е.
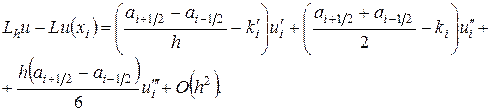
Отсюда видно, что 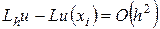 , если выполнены условия
, если выполнены условия
 ,
, 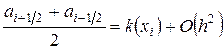 . (1.3)
. (1.3)
Условия (1.3) называются достаточными условиями второго порядка аппроксимации. При их выводе предполагалось, что функция  имеет четвертую производную и
имеет четвертую производную и  дифференцируемая функция. Показать, что условиям (1.3) удовлетворяют, например, следующие функции:
дифференцируемая функция. Показать, что условиям (1.3) удовлетворяют, например, следующие функции:
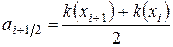 ,
,  ,
,
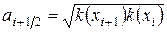 ,
, 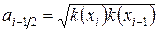 .
.
Рассмотрим разностную аппроксимацию оператора Лапласа
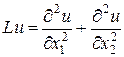 . (1.4)
. (1.4)
Введем на плоскости 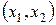 прямоугольную сетку с шагом
прямоугольную сетку с шагом 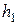 по направлению
по направлению  и с шагом
и с шагом 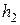 по направлению
по направлению  , т.е. множество точек
, т.е. множество точек
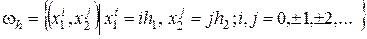
и обозначим
 ,
,  .
.
Из предыдущих рассуждений следует, что разностное выражение
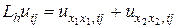 (1.5)
(1.5)
аппроксимирует дифференциальное выражение (1.4) со вторым порядком, т.е.  . Более того, для функции
. Более того, для функции  , обладающей непрерывными шестыми производными, справедливо разложение
, обладающей непрерывными шестыми производными, справедливо разложение
 .
.
Разностное выражение (1.5) называется пятиточечным разностным оператором Лапласа, так как оно содержит значения функции  в пяти точках сетки, а именно в точках
в пяти точках сетки, а именно в точках 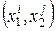 ,
, 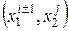 ,
, 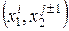 . Указанное множество точек называется шаблоном разностного оператора. Существуют и другие шаблоны.
. Указанное множество точек называется шаблоном разностного оператора. Существуют и другие шаблоны.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 398; Нарушение авторских прав?; Мы поможем в написании вашей работы!