Скорость при неравномерном движении

Свободное падение тел. Ускорение свободного падения

Перемещение при прямолинейном равноускоренном движении

Ускорение. Равноускоренное движение

Скорость при неравномерном движении

Прямолинейное неравномерное движение

Тема 1.1.3

САМОЕ ВАЖНОЕ В ПЕРВОЙ ГЛАВЕ

Явление механического движения состоит в том, что положение тел относительно других тел, т. е. их координаты, с течением времени изменяется.

Для определения положения тела (его координат) в любой момент времени нужно знать начальные значения его координат и вектор перемещения, потому что изменения координат как раз и равны проекциям вектора перемещения на соответствующие координатные оси.

Чтобы найти вектор перемещения, нужно знать скорость.

При прямолинейном равномерном движении скорость — величина постоянная, равная отношению вектора перемещения тела к промежутку времени, за который перемещение совершено.

Если направить координатную ось вдоль прямой, по которой происходит движение (в направлении движения или против него), то положение тела определяется всего одной координатой. Эта координата (например, х) вычисляется по формуле х= х₀ + v_xt, где х₀ — начальная координата и v_x — проекция скорости движения v на координатную ось X.

Движение относительно. Это значит, что перемещение, скорость, траектория движения различны относительно разных систем координат.

Относителен и покой. Абсолютно покоящихся тел не существует: тело, покоящееся относительно одной системы координат, движется относительно каких-то других систем. Материя существует только в движении.

Прямолинейное равномерное движение, т. е. движение с постоянной (по модулю и направлению) скоростью, не очень часто встречается на практике. Гораздо чаще приходится иметь дело с такими движения, при которых скорость движения со временем изменяется называются неравномерными.

Неравномерно движутся обычно автомобили, самолеты и т. д.

Неравномерно движутся падающие тела, тела, брошенные вверх.

При неравномерном движении определять перемещение по формуле s = vt уже нельзя, потому что скорость в разных местах траектории и в разные моменты времени различна. Как же определить перемещение тела, а значит, и его координаты при неравномерном движении? Что такое скорость при неравномерном движении?

Средняя скорость.

В некоторых случаях, когда имеют дело с неравномерным движением, пользуются средней скоростью. Ее получают, разделив перемещение тела s на время, в течение которого оно совершено:

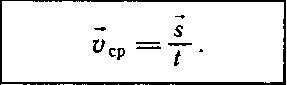
Если, например, поезд, двигаясь по прямой, проходит 600 км за 10 ч, то это значит, что в среднем он за каждый час проходит 60 км. Но ясно, что какую-то часть времени поезд вовсе не двигался, а стоял на остановке; трогаясь со станции, поезд увеличивал свою скорость, приближаясь к ней — уменьшал ее. Все это при определении средней скорости мы не принимаем во внимание и считаем, что поезд каждый час проходил по 60 км, каждые полчаса — по 30 км и т. д. Пользуясь формулой v_cp= s: t мы как бы

считаем, что поезд двигался равномерно со скоростью 60 км/ч, хотя, быть может, за все эти 10 ч не было ни одного такого часа, за который поезд прошел бы именно 60 км.

Знание средней скорости позволяет найти перемещение по формуле

s = v_cp s t

Но надо помнить, что эта формула дает верный результат только для того участка траектории, для которого определена средняя скорость. Если, пользуясь значением средней скорости в 60 км/ч, вычислять перемещение поезда не за 10 ч, а за 2, 4 или 5 ч, то мы получим неверный результат. Средняя скорость за время 10 ч не равна средним скоростям за 2, 4 или 5 ч.

Таким образом, средняя скорость, вообще говоря, не позволяет вычислять перемещение, а значит, и координаты в любой момент времени.

Для вычисления положения тела в любой момент времени скорость все-таки нужно знать, но не среднюю, а так называемую мгновенную скорость.

Мгновенная скорость.

Всякое движущееся тело обладает скоростью. С другой стороны, при своем движении по траектории тело проходит через все ее точки. А таких точек бесконечно много. Через каждую из них тело проходит в определенный момент времени. Таких моментов времени тоже бесконечно много. Выходит поэтому, что в каждый момент времени и в каждой точке траектории тело обладает какой-то скоростью. Вот эта скорость и называется мгновенной. Мгновенной скоростью тела называется скорость тела в данный момент времени или в данной точке траектории.

При прямолинейном равномерном движении скорость тела равна отношению его перемещения к промежутку времени, за который это перемещение совершено. Этому отношению равна и средняя скорость при неравномерном движении. Оно же поможет нам понять и смысл мгновенной скорости.

Допустим, что некоторое тело (как всегда, мы имеем в виду определенную точку тела) движется прямолинейно, но не равномерно. Нас интересует мгновенная скорость, например, в точке А его траектории (рис. 37). Выделим небольшой участок 1 на этой траектории, включающий точку А. Малое перемещение тела на этом участке обозначим через S₁, а малый промежуток времени, в течение которого оно совершено, через t₁. Разделивs на t, мы получим среднюю скорость на этом участке; это именно средняя скорость, потому что скорость непрерывно изменяется, и в разных местах участка она разная.

Уменьшим теперь длину участка. Выберем участок 2 (см. рис. 37), тоже включающий точку А. Перемещение теперь равно s₂ (s_{2 <}s₁), и совершает его тело за меньший промежуток времени t₂. На этом участке скорость успевает измениться на меньшую величину. Но отношение S₂: t₂

— дает нам и теперь среднюю скорость на этом меньшем участке. Еще меньше изменение скорости на протяжении участка 3 (также включающего в себя точку А), меньшего, чем участки 1 и 2. Разделив перемещение s₃ на промежуток времени t₃, мы опять получим среднюю скорость на этом малом участке траектории.

Будем продолжать уменьшать промежуток времени, за который мы рассматриваем перемещение тела. Вместе с ним будет уменьшаться и перемещение. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным).

Участок траектории, пройденный за этот, совсем уже малый, промежуток времени как бы стянется в точку А, а промежуток времени — в момент времени. Тогда-то средняя скорость и станет мгновенной скоростью тела в точке А.

Мгновенная скорость, или скорость в данной точке, равна отношению достаточно малого перемещения на участке траектории, включающем эту точку, к малому промежутку времени, в течение которого это перемещение совершается.

Мгновенная скорость — это векторная величина. Направление вектора мгновенной скорости совпадает с направлением движения в данной точке. В дальнейшем, говоря о скорости неравномерного движения, мы будем иметь в виду именно мгновенную скорость.

О мгновенной скорости можно говорить и в случае равномерного движения. Разница только в том, что при равномерном движении мгновенная скорость в любой точке и в любой момент времени одна и та же. При неравномерном же движении она в разных точках и в различные моменты времени различна.

Прием, к которому мы прибегли, чтобы пояснить смысл мгновенной скорости, состоит, таким образом, в следующем. Участок траектории, включающий интересующую нас точку и время, в течение которого он проходится, мы мысленно постепенно уменьшаем до тех пор, пока участок уже нельзя отличить от точки и неравномерное движение от равномерного. Таким приемом всегда пользуются, когда исследуются явления, в которых играют роль непрерывно изменяющиеся величины.

Упражнение 5

1. Половину времени при переезде одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?

Дата добавления: 2014-01-14