Общие замечания. Система статически устойчива, если при изменении (увеличении) частоты от нуля до бесконечности конец характеристического вектора начертит в комплексной

Система статически устойчива, если при изменении (увеличении) частоты от нуля до бесконечности конец характеристического вектора начертит в комплексной плоскости кривую (годограф), проходящую последовательно без пропусков столько квадрантов, какова степень характеристического уравнения.

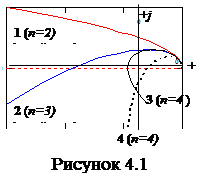
В качестве примера на рис.4.1 приведены типичные годографы систем для характеристических уравнений различных степеней годографы, полученные по (4.4).

Как следует из анализа рис.4.1 кривые 1, 2 и 3 соответствуют устойчивому состоянию систем, описываемых соответственно уравнениями второго, третьего и четвертого порядков. Кривая 4, соответствующая характеристическому уравнению четвертой степени, свидетельствует о нарушении статической устойчивости электрической системы.

4.2.3 Выделение областей устойчивости (метод D-разбиения)

Часто важно знать, в каких пределах можно изменять те или иные параметры системы не нарушая ее устойчивости. Это определенным образом характеризует запасы статической устойчивости. Целью исследований, в этом случае, является отыскание всех значений исследуемых параметров, при которых система устойчива.

Поясним это на примере уравнения второй степени:

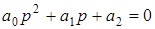. (4.5)

Пусть изображающая точка М в плоскости координат a₁, a₂ перемещается из точки М₁ в точку М₂ (рис.4.2).

В соответствии с этим корни характеристического уравнения перемещаются от значений 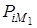к значениям 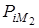. Совокупность коэффициентов a_k, при которых хотя бы один или пара комплексных корней находятся на мнимой оси, определяет собой кривую N в пространстве коэффициентов. Если траектория точки М пересечет поверхность N, то траектория корней пересечет мнимую ось. В рассматриваемом частном случае для уравнения второго порядка кривой N является ось действительных чисел.

Таким образом, поверхность N делит пространство коэффициентов a_k на области D(m) с одинаковым числом (m) корней в правой и (n-m) в левой полуплоскости корней.

Такое разбиение называют D-разбиением. Следовательно, кривая N является границей D-разбиения. Граница D-разбиения является отображением мнимой оси комплексной плоскости корней характеристического уравнения.

Рассмотрим порядок D-разбиения по одному параметру.

Пусть имеется характеристическое уравнение, в которое входит линейно один параметр k.

1. Преобразуем характеристическое уравнение так, чтобы разделить члены содержащие k и не содержащие:

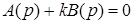. (4.6)

2. Решим уравнение (4.6) относительно k

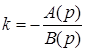. (4.7)

3. Подставим вместо 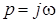и отделим вещественную часть от мнимой:

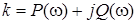. (4.8)

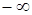4. Задаемся значениями от до 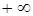и строим в плоскости коэффициента k кривую – границу D-разбиения.

Чтобы знать, по какую сторону границы находится возможная область устойчивости границу штрихуют согласно правила: при движении от 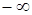к 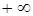штриховка осуществляется слева, и наоборот. В плоскости одного параметра при переходе через границу D-разбиения со стороны заштрихованной области в не заштрихованную в плоскости корней характеристического уравнения один корень переходит слева на право и наоборот.

Пример:

Пусть имеем характеристическое уравнение

.

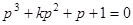Решив его относительно k, получим

.

Выполнив подстановку 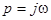, получим зависимость коэффициента от частоты:

.

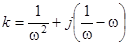Задаваясь значениями частоты от 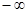до 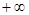получим области статической устойчивости, показанные на рис.4.3.

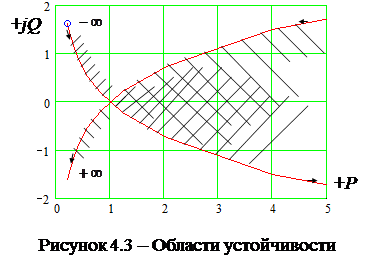Претендентом на область устойчивости является значения 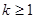в зоне двойной штриховки.

Действительно, при 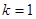исходное уравнение имеет вид

.

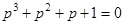Разложив на множители, получим

.

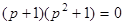Корни имеют следующие значения:

P₁=1; P₂=+j; P₃=-j.

В начальный момент КЗ значение тока в любой цепи, имеющей индуктивность, остается неизменным и равным его значению в конце предшествующего режима. Однако при исследовании переходных процессов ток в произвольный момент времени представляют как сумму периодической и апериодической составляющих и определение каждой из них является важной задачей.

При расчете начального значения периодической составляющей тока трехфазного короткого замыкания в электроустановках напряжением свыше 1 кВ должны быть учтены все синхронные генераторы и компенсаторы, а также синхронные и асинхронные электродвигатели мощностью 100 кВт и более, если они не отделены от точки КЗ токоограничивающими реакторами или силовыми трансформаторами.

Начальное значение периодической составляющей тока КЗ от СГ или СК можно получить, решив уравнения Парка-Горева и полученное выражение t= 0. Однако, проще процесс в начальный момент КЗ исследовать, исходя из принципа сохранения потокосцеплений контуров ротора СМ в момент любого нарушения режима. Кроме того, такой подход позволяет более наглядно выявить, какими ЭДС и сопротивлениями следует характеризовать СМ в начальный момент КЗ.

Дата добавления: 2014-01-11