Показатели вариации. понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Средняя величина, как уже отмечалось, - это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало I нее отличаются. В таких случаях средняя хорошо представляет всю совокупность. В других, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность. В нашем примере (табл. 7.1 и 7.2) в первом регионе средняя характеристика более надежна, более типична, чем во втором регионе; объем товарооборота в среднем на одно предприятие, который складывался под влиянием более разнообразных условий, и изучаемая совокупность менее однородны, а средняя величина менее надежна.

Колеблемость отдельных значений характеризуют показатели вариации.

Термин "вариация" произошел от латинского variatio-изменение, колебле­мость, различие. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделенной совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц х. к средней измеряется рядом абсолютных, средних и относительных показателей.

Абсолютные и средние показатели вариации и способы их расчета. Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации, определяемый как разность между наибольшим 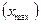и наименьшим 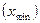значениями вариантов:

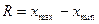(7.1)

Рассмотрим колеблемость показателей объема товарооборота в среднем на одно предприятие (см. табл. 7.1 и 7.2).

Однако показатель размаха вариации составил:

регион 1: R= 130 - 90=40 млн. руб.;

регион 2: R= 180- 60= 120 млн. руб.

Сравнение показателей в нашем примере свидетельствует, что размах вариации объема товарооборота выше в регионе 2. Но он улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду. Однако легкость вычислений и простота истолкования обусловили широкое применение этого показателя.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение 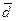, которое учитывает различия всех единиц изучаемой совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:

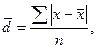(7.2)

или

(7.3)

Таблица 7.1

Дата добавления: 2014-01-11