Произвольной формы

ДЛЯ СЛУЧАЯ ОБТЕКАНИЯ ЦИЛИНДРИЧЕСКОГО ТЕЛА

ТЕОРЕМА ЖУКОВСКОГО О ПОДЪЕМНОЙ СИЛЕ

Выше была доказана теорема Жуковского для частного слу­чая обтекания идеальной жидкостью кругового цилиндра беско­нечной длины.

Теперь рассмотрим обтекание плоским потоком произвольно-то тела и докажем, что теорема Жуковского справедлива и для данного случая.

Если предположить, что вне цилиндра поток является без­вихревым (потенциальным), то согласно теореме Стокса цирку­ляция скорости по любому замкнутому контуру, охватывающему обтекаемый цилиндр, будет иметь одну и ту же для всех конту­ров величину, которую мы обозначим через Г. Проведем далее вокруг цилиндрического тела произвольной формы замкнутый контур S (рис. 6.9). Применим к жидкому объему, заключенно­му между поверхностью тела Lи произвольной поверхностью S, которую мы будем называть конт­рольной, теорему о количестве дви­жения.

Рис. 6.9. К доказательству теоремы Жуковского для произвольного плоского кон­тура

Поскольку вес жидкости в выде­ленном объеме уравновешивается из­менением по высоте сил давления, рас­пределенных по контрольной поверх­ности, то мы не учитываем силу веса и весовое давление, т. е, рассматри­ваем среду как невесомую. Кроме этих сил, на выделенный объем жидкости действует реакция со стороны тела и давления, распределенные по контроль­ной поверхности, силы трения не учи­тываем (жидкость идеальная).

Определим количество движения, выносимое из выделенного объема за единицу времени, сквозь контрольную поверхность. Выделим на контрольной поверхности S элементарную пло­щадку ds*l и проведем к ней внешнюю нормаль п, которая об­разует с осями координат углы α и β (см. рис. 6.9), Если проек­цию скорости частиц, протекающих через площадку ds*l, на нормаль η обозначить через V_n, то, очевидно, что масса жидкос­ти, протекающей в единицу времени сквозь эту площадку, будет равна rV_ndsl. Соответственно количество движения, переноси­мое этой массой, запишется r 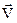V_nds. Количество движения рас­сматриваемой массы жидкости, переносимое в единицу времени сквозь всю контрольную поверхность, выразится интегралом . Проекции этого количества движения на координатные оси соответственно равны

,

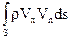Определим теперь действующие на выделенный объем жид­кости внешние силы и их проекции на координатные оси. Сoстороны окружающей жидкости на контрольную поверхность действуют силы давления, направленные перпендикулярно к по­верхности. Сила, приложенная к площадке ds*1, равна pds, проекции ее на оси координат соответственно равны - ρ cos a ds и - p cos b ds. Следовательно, ,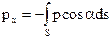

Со стороны внутренней границы выделенного объема жидкости на тело действуют нормальные силы давления, приложенные к поверхности тела L.В таком случае согласно третьему закону Ньютона со стороны тела на окружающую жидкость действуют силы, равные им по величине, но имеющие обратное направление. Если проекции результирующей силы, действующей на тело со стороны окружающей его жидкости, обозначить через X и Y, то проекции силы реакции со стороны тела будут равны – X, -Y. Импульсы этих сил за единицу времени будут -X и -Y. Изме­нение количества движения на поверхности выделенного объема жидкости за единицу времени равно по законам механики сум­ме приложенных к поверхности внешних сил. В проекциях на оси координат эта теорема запишется в виде

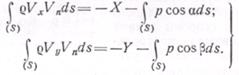
(6. 23)

Соответственно силы, действующие на тело со стороны окру­жающей его жидкости, определяются следующим образом:

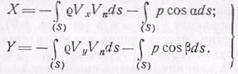
(6.24)

Таким образом, для определения силы лобового сопротивле­ния тела X и подъемной силы У необходимо знать давление и скорость в каждой точке контрольной поверхности. Подставив в интегралы соотношений (6.24) значение давления, определен­ное по формуле Бернулли (5.25) с учетом равенства соs b = = sin α, получим

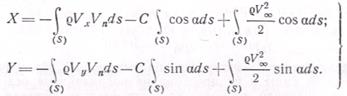
(6. 25)

В этих равенствах вторые интегралы равны нулю, так как

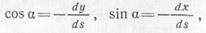
ά при обходе по замкнутому контуру S переменные χ и у возвра­щаются к своему первоначальному значению. Итак,

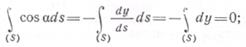
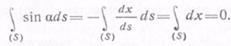
Таким образом, равенства (6.25) принимают вид

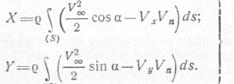(6.26)

Следует отметить, что формулы (6.26) получены для случая несжимаемой жидкости. Когда скорость невозмущенного потока направлена по оси ОХ и равна V_¥, потенциал скорости можно записать в виде j = V_¥ x+ j'(x, у), (6.27)

где φ'(x, у) - потенциал добавочных возмущенных скоростей, удовлетворяющих уравнению Лапласа. Учитывая выражения (6,27), для проекций скорости V_x, V_y получим соотношения:

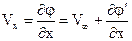(6.28)

(6. 29)

Функции φ'(x, у) па бесконечности удовлетворяют условиям

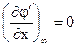, (6.31)

Выражение для скорости V_n

с учетом (6.28) и (6.29) принимают вид

Полагая, что контур 5 настолько велик, что в силу условий (6.30) величинами (д j' /д х )^г и

(дj'/ду)² можно пренебречь, оп­ределим произведения V _nV_Х и V_nV_v:

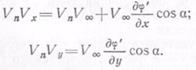
С учетом этих выражений равенство (6.26) принимает вид

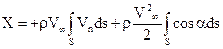
Интеграл 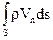представляет собой расход жидкости сквозь замкнутый контур.

Поскольку внутри контура отсутству­ют источники или стоки, этот интеграл равен нулю. Кроме то­го, из геометрических соображений следует cos a ds = 0.

Таким образом X = 0, т.е. сила лобового сопротивления тела, обтекае­мого плоскопараллельным потоком идеальной жидкости, равна нулю. Этот результат (парадокс Даламбера — Эйлера) мы уже получили в частном случае для кругового цилиндра. Перейдя ко второму равенству (6.26), будем иметь

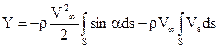
где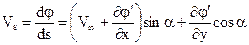

Первый член этого равенства равен нулю, а второй согласно (4.7) представляет собой циркуляцию скорости по замкнутому контуру, следовательно,

Y = -rV_¥Γ. (6.32)

Результат, выражаемый формулой (6.32), обычно формули­руется в виде теоремы Жуковского: если поток, имеющий в бес­конечности скорость V_¥, обтекает контур, и циркуляция скорос­ти по этому контуру равна Г, то равнодействующую сил давле­ния жидкости на контур получим, если умножим вектор, пред­ставляющий скорость потока в бесконечности, на циркуляцию скорости и на плотность жидкости. Таким образом, получена формула для определения подъемной силы единицы длины ци­линдрического тела бесконечного размаха. Знак минус, стоящий в правой части формулы, дает возможность установить направ­ление действия силы" Если знаки V_¥ и Г различны, то сила будет положительна и направлена вверх, при одинаковых знаках V_¥ и Г подъемная сила направлена вниз.

Следует отметить, что при доказательстве теоремы предпо­лагалось, что поток, обтекающий тело, плоскопараллельный. Таким можно считать поток, обтекающий цилиндрическое крыло бесконечного удлинения.

Из теоремы Жуковского следует: для получения подъемной силы тела произвольной формы, обтекаемого плоскопараллельным потенциальным потоком, необходимо обеспечить такое ско­ростное поле, при котором циркуляция скорости по замкнутому контуру вокруг крыла была бы отлична от нуля. Для кругового цилиндра, обтекаемого вязким потоком, этого можно достичь вращением цилиндра. В идеальном невязком потоке в этом не­обходимости нет — соответствующим подбором формы тела с заостренной задней кромкой можно добиться его обтекания с циркуляцией Г^О. Эта циркуляция будет создаваться не реаль­ным, а фиктивным вихрем. Жуковский назвал его «присоединен­ным». Очевидно, что Г — есть циркуляция скорости, обусловлен­ная наличием вихря.

Таким образом, при определении подъемной силы можно представить себе крыло замененным одним или несколькими присоединенными вихрями, которые будучи неподвижно связаны с крылом, создают в потоке такую же циркуляцию скорости по любому замкнутому контуру, охватывающему крыло, какую в действительности создает крыло. На возможность замены тела эквивалентной системой присоединенных вихрей указал впервые Жуковский еще в 1905 году. Эта идея Жуковского оказалась ис­ключительно плодотворной для решения многих практических задач не только в авиастроении, но и в турбостроении, корабле­строении и др.

Теорема Жуковского указывает также путь повышения подъ­емной силы крыла при данной скорости его движения в потоке путем увеличения циркуляции скорости по контуру, охватываю­щему крыло.

Циркуляцию же можно увеличить различными способами, например, увеличением кривизны крыла, воздействием на погра­ничный слой, приведением в движение части поверхности крыла и т.д. В общем случае, при движении тела в жидкости, циркуля­ция скорости вокруг него будет изменяться с течением времени. Если циркуляция скорости по произвольному контуру, охваты­вающему тело, переменна во времени, то такой поток не может быть везде потенциальным. Он должен содержать отдельные или непрерывно распределенные вихри.

Теорема Жуковского для случая произвольного движения крыла в идеальной несжимаемой жидкости была доказана Л, И. Седовым [58].

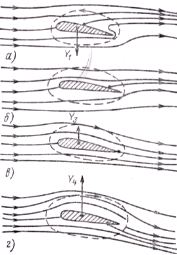6.5. ВОЗНИКНОВЕНИЕ ЦИРКУЛЯЦИИ СКОРОСТИ

Дата добавления: 2014-11-06