Метод потенціалів

Алгоритм знайдення оптимального плану транспортної задачі:

1. Для даного опорного плану підбираємо потенціали рядків і потенціали стовпців 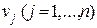таблиці постачань так, щоб для кожної заповненої клітини їхня сума дорівнювала відповідній вартості перевезення одиниці товару (числу, записаному у лівому верхньому куті клітини):

,

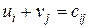де i – номер рядка, j – номер стовпця, яким належить заповнена клітина. Для визначення потенціалів один з них вважається рівним нулю.

2. Для кожної незаповненої клітини послідовно обчислюємо оцінки

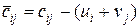, (5.1)

де i – номер рядка, j – номер стовпця, яким належить незаповнена клітина; – потенціали, знайдені в п. 1 алгоритму. Оцінки для заповнених клітин вважаються рівними нулю. Складаємо матрицю оцінок.

3. Перевіряємо виконання критерію оптимальності. Якщо оцінки всіх незаповнених клітин невід’ємні (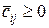), то знайдений розподіл є оптимальний – рішення закінчене. Якщо серед оцінок незаповнених клітин є від’ємні, то
будуємо новий опорний план.

4. Обираємо клітину з найменшою оцінкою для переведення в неї постачання. Для обраної незаповненої клітини будуємо цикл перерахування – зв’язну ламану, одна з вершин якої лежить у незаповненій клітині, інші – у заповнених, а її ланки – уздовж рядків і стовпців таблиці. У вершинах циклу розставляємо знаки “+” і “–” так, щоб у незаповненій клітині стояв знак “+”, а сусідні вершини мали протилежні знаки. Постачання z, що визначається як мінімум серед постачань у клітинах зі знаком “–”, пересуваємо за циклом. У результаті постачання в клітинах циклу зі знаком “+” збільшиться на z, а в клітинах зі знаком “–” зменшиться на z. Клітина, постачання в якій при цьому дорівнюватиме нулю, буде вважатися незаповненою, інші клітини циклу – заповненими. Таким чином одержуємо новий опорний план.

5. Переходимо до п. 1 алгоритму.

Задача 5.4. Знайти у транспортній задачі 1.3 (с. 10) оптимальний розподіл постачань і мінімальні витрати на перевезення.

Дата добавления: 2014-11-06