Основы синтеза аналоговых и дискретных фильтров

Большое практическое значение имеют методы синтеза ЦФ с требуемым видом импульсной или частотной характеристик ЦФ. Рассмотрим некоторые приемы синтеза ЦФ по заданным характеристикам их аналоговых прототипов.

Синтез по заданной импульсной характеристики аналогового прототипа g (t)

ЦФ строится с импульсной характеристикой, которая является результатом дискретизации g (t), т. е. ее k -й отсчет g (k)= g (k Δ). Если в импульсной характеристике ЦФ ограничиться конечным числом слагаемых, получаем реализацию в виде трансверсального фильтра. При неограниченном числе компонентов g (k) следует реализация в виде рекурсивного фильтра.

Синтез ЦФ по заданной частотной характеристике K (j ω) (или операторного коэффициента передачи K (p))

Принципиально нельзя создать ЦФ, частотная характеристика которого Кцф (ω_ц) повторяла бы частотную характеристику аналогового прототипа К (ω_а), так как Кцф (ω_ц) является периодической функцией частоты дискретизации ω_g. Однако можно потребовать, чтобы весь интервал частот ωа, характеризующий аналоговую цепь, был преобразован в отрезок частот ωц ЦФ, на котором сохраняется

форма характеристики К (ω_а), причем

Если для перехода от р-плоскости (отображающей аналоговый прототип) к z-плоскости (отображающей цифровой фильтр) воспользоваться соотношениями

то формально мы от частотной характеристики аналогового эквивалента переходим к системной функции ЦФ. Однако, если 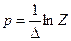подставить в выражение для передаточной функции аналогового прототипа К (р), которая для цепей с сосредоточенными параметрами представляет собой отношение двух полиномов от Р (дробно-рациональную функцию), получим физически нереализуемую системную функцию ЦФ, так как она не выражается отношением двух полиномов от z.

Надо найти такое преобразование Р в Z, которое привело бы к реализуемому фильтру, но вместе с тем сохраняло бы основное свойство преобразования (12.1), т. е. переводило бы точки мнимой оси на плоскости Р (точки j ω) в точки единичной окружности на z-плоскости.

Для синтеза ЦФ получило широкое распространение билинейное преобразование

Для выяснения сущности преобразования (12.2) положим

т. е. комплексно-значные точки z лежат на единичной окружности и характеризуются аргументом (угловым сдвигом) ω_ПΔ. Тогда правая часть (12.2) принимает вид

Воспользовавшись формулами

(12.3) можно представить так:

Последнему соотношению согласно (12.2) соответствует мнимая аналоговая часть вида jω_а, следовательно,

При выполнении неравенства

следует, что

В более общем случае надо учесть изменение масштаба по оси частот ЦФ.

Дата добавления: 2014-11-06