P.S. Не забудьте прихватить с собой небольшой сувенирчик. Будем обмениваться подарками. 4 страница

§ 22, Упругие волны в изотропной среде

Если в деформируемом теле происходит движение, то темпера­тура тела, вообще говоря, отнюдь не постоянна, а меняется как со временем, щк и от точки к точке вдоль тела. Это обстоятельство сильно усложняет точные уравнения движения в общем случае произвольных движений.

Обычно, однако, положение упрощается благодаря тому, что передача тепла из одного участка тела в другой (посредством про­стой теплопроводности) происходит очень медленно. Если тепло­обмен практически не происходит в течение промежутков времени порядка периода колебательных движений в теле, то можно рас­сматривать каждый участок тела как теплоизолированный, т. е. движение будет адиабатическим. Но при адиабатических деформа­циях a_lk выражается через и_ш по формулам обычного вида с той лишь разницей, что вместо обычных (изотермических) значений величин Е, а надо брать их адиабатические значения (см. § 6). Ниже мы будем считать это условие выполненным, и соответст­венно этому под Е и а в этой главе будут подразумеваться их адиабатические значения.

Для того чтобы получить уравнения движения упругой среды, надо приравнять силу внутренних напряжений da_thldx_h произ­ведению ускорения u_t на массу единицы объема тела, т. е. на его плотность р:

p**=ilr- (ад

¹) Подразумевается, что скорость v точек среды совпадает с производной и от ее смещения. Подчеркнем, однако, что отождествление этих двух величин отнюдь не является чем-то само собой разумеющимся. В кристаллах вектор и представляет собой смещение узлов решетки; скорость же v определяется в ме­ханике сплошных сред как импульс единицы массы вещества. Равенство v = и справедливо, строго говоря, лишь для идеальных кристаллов, где в каждом узле решетки (и только в них) находится по атому. Если же кристалл содержит дефекты (незаполненные.узлы — вакансии, или же, напротив, лишние атомы в междоузлиях), то перенос массы относительно решетки (т. е. отличный от нуля импульс) может существовать и в недеформированной решетке — за счет диффузии дефектов «сквозь решетку». Отождествление v и и подразумевает прене­брежение этими эффектами — в связи с медленностью диффузии или малой концентрацией дефектов.

Это — общий вид уравнений движения ^г).

В частности, уравнения движения изотропной упругой среды можно написать непосредственно по аналогии о уравнением рав­новесия (7,2). Имеем

Р" = ТТГТ^)- ^AU + 2(1+0)^(1-20 S^{rad diV} (²²'²)

Поскольку все деформации предполагаются малыми, то рас­сматриваемые в теории упругости движения представляют собой малые упруеие колебания или волны. Начнем с рассмотрения пло­ской упругой волны в неограниченной изотропной среде, т. е. волны, в которой деформация и является функцией только от одной из координат, скажем, от х (и qt времени). B<ie производные по у и z в уравнениях (22,2) исчезают, и мы получаем для отдель­ных компонент вектора и следующие уравнения:

д²и_х 1 д*и_х _ _n dbiy _____ 1 d²"gf _ _n „.

дх* ~ с\ di* ' ^Uj дх* cj dt* £~ ^и ^ ' >

(уравнение для u_z такое же, как для и_у), где введены обозна­чения ¹):

°^{l =} [р(1 + а)(1-2о) ] ' ' °^t= Up Да) ] ' * ⁽²²'⁴⁾

Уравнения (22,3) представляют собой обычные волновые урав­нения в одном измерении, и входящие в них величины с_г и c_t являются скоростями распространения волны. Мы видим, что скорость распространения волны оказывается различной для компоненты и_х, с одной стороны, и компонент щ, и_г — с другой.

Таким образом, упругая волна представляет собой по суще­ству две независимо распространяющиеся волны. В одной из них (и_х) смещение направлено вдоль распространения самой волны; такую волну называют продольной, она распространяется со ско­ростью Ci. В другой (и_у, u_z) — смещение направлено в плоскости, перпендикулярной направлению распространения; такую волну называют поперечной, она распространяется со скоростью c_t. Как видно из (22,4), скорость с_г всегда больше скорости c_t ²):

_Ci>(4/3)V2_C<. (22,5)

¹) Дадим также выражения скоростей ci и С(через коэффициенты сжатия и сдвига и через коэффициенты Ламэ: / ЗК + 4ц. у/2 /Я + 2ц, у/2 /МЛ¹/^{2 а}) При фактическом изменении о в пределах от 0 до 1/2 (см. примечание на стр. 26) имеет место и более сильное неравенство ц > cj j^2,

Скорости с_г и Ct называют продольной и поперечной скоростями звука.

Мы знаем, что изменение объема при деформации определяется суммой диагон&&йъ1Х членов тензора деформации, т. е. величиной Hjj = div и. В поперечной волне имеются только компоненты u_v, щ, и поскольку они не зависят ни от у, ни от г, для такой волны div и = 0. Таким образом, поперечные волны не связаны с избие­нием объема отдельных участков тела. Напротив, для продольных волн div и Ф 0; эти волны сопровождаются сжатиями и расши­рениями в теле.

Разделение волны на две независимо распространяющиеся с разными скоростями части можно произвести и в общем случае произвольной (не плоской) упругой волны в неограниченном про­странстве.

Перепишем уравнение (22,2), введя в него скорости e_t и c_t'
и = с? Ли + (с²-cf) grad div и. (22,6)

Представим вектор а в виде суммы двух частей:

и = щ + щ, (22,7)

из которых одна удовлетворяет условию

div щ = 0, (22,8)

а другая — условию

rot щ = 0. (22,9)

Из векторного анализа известно, что такое представление всегда возможно (это есть представление вектора в виде суммы ротора некоторого вектора и градиента некоторого скаляра). При подстановке и = щ + щ в (22,6) получаем

, и/ +»ь = с\ Д (и, + и,) + (с| - с|) grad div и,. (22,10)

Применим к обеим сторонам этого уравнения операцию div. Поскольку div u₍ == 0, мы получим

div щ = ct Д div ti/ -j- (cf — с?) Д div u,,

или

div {щ — с] Smi) = 0.

С другой стороны, rot стоящего в скобках выражения тоже равен нулю в силу (22,9). Но если rot и div некоторого вектора исче­зают во всем пространстве, то этот вектор тождественно равен нулю. Таким образом,

*£--с?Ди, = 0. (22,11)

Аналогично применяя к уравнению (22,10) операцию rot и помня, что rot Uj = 0 и что rot всякого градиента равен нулю, находим

rot(tb — с) Ди*) — 0.

Поскольку div стоящего в скобках выражения тоже равна нулю, то мы приходим опять к уравнению того же вида^как и (22,11);

-gL__c?Au, = 0. (22,12)

Уравнения (22,11) и (22,-12) предс^анляют 'Собой обычные вол­новые уравнения (в трех измерениях). Каждое" цз них соответствует распространению упругой волны со скоростью соответственно Cj или c_t. Одна из этих волн (щ) не связана с изменением объема (в силу div щ — 0), а другая (а_г) сопровождается объемными сжа­тиями и расширениями.

В монохроматической упругой волне вектор смещения имеет вид

и = Ъе{щ(г)е~™\, (22,13)

где и₀ — функция координат. Эта функция удовлетворяет урав­нению

с] Au₀ + (^с/ — ^с?) grad div u₀ + <o²u₀ = 0, (22,14)

получающемуся при подстановке (22,13) в (22,6). Продольная и поперечная части монохроматической волны удовлетворяют урав­нениям

Au^+fefo-O, Ди/+ ftfn,=0, (22,15)

где ki — ю/cz, k_t = ®к_г — волновые векторы продольной и попе­речной волн.

Наконед, рассмотрим отражение и преломление плоской моно­хроматической уяругой волны на границе раздела между двумя различными упругими средами. При этом надо иметь в виду, что при отражении и преломлении характер волны, вообще говоря, меняется. Если на границу раздела падает чисто поперечная или чисто продольная волна, то в результате получаются смешан­ные волны, содержащие как поперечные, так и продольные части. Характер волны не меняется (как это явствует из соображений симметрии) только в случае перпендикулярного падения еолны на поверхность раздела и в случае падения под произволыгь™ углом поперечной волны с параллельными плоскости раздела колеба­ниями.

Соотношения, определяющие направления отраженной и пре­ломленной волн, могут быть получены непосредственно из постоян­ства частоты и касательных к поверхности раздела компонент волнового вектора *). Пусть 0 и 6' — угол падения и угол отра­жения (или преломления), г с, с' — скорости обеих рассматри­ваемых волн. Тогда

■^г = А-. (22,16)

¹) См. VI, § 66. Все изложенные там соображения полностью применимы и здесь.

sme с v > /

Пусть, например₊ падающая волна поперечна. Тогда о = c_tt есть скорость поперечных волн в первой среде. Для поперечной же отраженной водаы имеем тоже с' = ct_tt и потому (22,16) даст

0 = 8',

т. е. угол падения равен углу отражения. Для продольной же отраженной всэдны имеем с' = ct_lt и потому

s|n0 _ Cfi

su10' ~ Сц '

Для поперечной части преломленной волны имеем с' = Ct% и при поперечной ш падающей волне имеем

sin 9 c_tl

sin 0' Cj₂

Аналогично двя продольной преломленной волны имеем

sin 8 cti

sine' ~ Ci_% '

Задачи

1. Определить коэффициент отражения продольной монохроматической волны, падающей под произвольным углом на границу тела с вакуумом.

Решение. При отражении под произвольным углом возникают как продольная, так и ^поперечная отраженные волны. Из соображений симметрии заранее ясно, что вектор смещения в поперечной отраженной волне будет лежать целиком в плоскости падения (рис. 20; п₀, п;, щ — еди­ничные векторы вдоль направлений падающей, продольной и поперечной отраженных волн, a u₀, и;, щ — соответству­ющие векторы смещений). Полное смещение в теле равно сумме (общий множитель е~^ш( для краткости опускаем)

и = ЛоПое'^к°^г -f A_tnie^iklT + A_t [ъщ] е'^к'^г

(а — единичный вектор, перпендикулярный к плоскости падения). Абсолютные величины волновых векторов равны: k₀ = ki = (n/ci, ki = Wcj, а углы падения 0_o

и отражения 6;, 0* связаны посредством 0; = 8₀, sin 0(= понент тензора деформации на границе тела получаем

и_хх = ik₀ (А₀ + А{) cos² 0_О + iA_tk_t cos 0j sin 0_t, uu = ik₀(A₀ + Ai),

Cf

sin 0„ —. Для ком-

■■ ik₀ (A₀ — Ai) sin 0_O cos 6₀ —- A_tk_t (cos^a Q_t ■

- sin² 0_t)

(сбщие экспоненциальные множители опускаем). Компоненты тензора напря-»кений вычисляем по общей формуле (5,11), которую удобно писать здесь в виде

°ik = ²P^cl^uik + Р (с? — ^2с?) ^и/А*«

Граничные условия на свободной поверхности среды гласят о^п^ = 0, откуда а_хх = Оу_Х = 0, и дают два уравнения, из которых можно выразить А\, At через А₀. В результате вычисления получается

с] sin 29, sin 26₀ + с) cos² 29, 2ciCt sin 26₀ cos 29f

с² sin 26, sin 20₀ — с] cos² 20,

Ai = А_а

A_t = —А₀

ci sin 26, sin 20₀ + l\ cos² 26,

При 9₀ = 0 имеем A\ = —А_й, At = 0, т. е. волна отражается целиком как про­дольная. Отношение перпендикулярной к поверхности среды компоненты плот­ности потока энергии в отраженной продольной волне к такому же потоку в па­дающей волне есть

^Rl-\A₀

Аналогичное отношение для отраженной поперечной волны есть

ct cos Of I At I²

ci cos 6₀ I A₀

Разумеется, Ri -f- Rt = 1.

2. To же, если падающая волна поперечная (и направление колебаний в ней
лежит в плоскости падения)*).

Решение. Волна отражается в виде поперечной же и продольной волн, причем Of = б₀, cj sin 9; = cj sin 9₀. Полный вектор смещения:

u = [ап„] Л₀е'^к°^Г + mAie^tklT + [an₍] A_te^kl^T.

Для амплитуд отраженных волн получаются выражения A_t с\ sin 29, sin 29₀ — с| cos² 29₀ "^7^_^sin26,sin29₀ + c.²cos²2e_Q '

At ________ 2c;c_t sin 29₀ cos 28₀

A₀ ~ c\ sin 29, sin 29₀ + cj cos² 20_o '

3. Определить частоты радиальных собственных колебаний упругого шара
радиуса R.

Решение. Выбираем сферические координаты с началом в центре шара. При радиальных колебаниях и направлено по радиусу и зависит только от г (и от t). Поэтому rot и = 0. Введем «потенциал» смещения <р согласно и_г = и = = ду/дг. Выраженное через <р уравнение движения сводится к волновому урав­нению с² Дф = ф, или для периодических по времени (~е"*^и') колебаний;

*»--И-("£)-[1] «

Решение, конечное во всем объеме шара, включая его центр, есть

, sin kr _{ф= А} —

(временной множитель не пишем). Радиальные напряжения:

°Yr = Р { iA ~ ²<$) «и + ^2с*^игг) = Р { (с? - Щ ^ДЧ> + 2c?q>" }

или, использовав уравнение (1):

—а„ = —со ш — 4с;— ш •
р ^{гг т 1} г ^т

Граничное условие а_гг (/?) = 0 приводит к уравнению
tg kR _________ 1

kR 1 — (kRa/2c_t)* '

(2)

(3)

Его корни определяют частоты собственных колебаний <о = с;й.

4. Определить частоту радиальных колебаний сферической полости в не­ограниченной упругой среде, для которой с; s> cj.

Решение. В неограниченной среде радиальные колебания полости сопровождаются излучением продольных звуковых волн, что приводит к потере энергии и тем самым к затуханию колебаний. При с; > cj (т. е. К > р.) это излу­чение будет слабым и можно говорить о собственных частотах колебаний с малым коэффициентом затухания.

Ищем решение уравнения (I) в виде расходящейся сферической волны

л ^еШ _h ">
ф=л, k =

г С), j

и с помощью (2) получаем из граничного условия a_rr (R) = 0

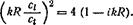
Отсюда (при С\ > с₍)

Вещественная часть о дает собственную частоту колебаний, а мнимая — коэф­фициент затухания; в несжимаемой среде (с_г оо) затухание, естественно, от­сутствовало бы. Эти колебания — специфический результат сопротивляемости среды по отношению к сдвигу (р, Ф 0). Обратим внимание на то, что для них kR = 2с*/с; <; 1, т. е. соответствующая этим колебаниям длина волны велика ио сравнению с R (интересно⁴ сравнить это с колебаниями упругой сферы, для которых при с; > ct первая собственная частота определяется согласно (3) из kR = я).

§ 23. Упругие волны в кристаллах

Распространение упругих волн в анизотропной среде, т. е. в кристаллах, подчиняется более сложным закономерностям, чем распространение волн в изотропном теле. Для исследования таких волн надо обратиться к общим уравнениям движения

и воспользоваться для a_ik общим выражением (10,3)

Соответственно сказанному в начале предыдущего параграфа под kikim ^наД° везде подразумевать адиабатические значения модулей упругости.

Подставляя o_lk в уравнения движения, получаем

j dtilmIjklm д f du_t, du_m \

___ 1» д^щ i 1 ₁ 6%_m

— ₂ л_{Шт ajCftdjCm} -r- ₂ ^лШт ax_ftdxi "

Поскольку тензор Я_Шт симметричен по индексам / и т, то, меняя во втором члене обозначение индексов суммирования / и т на об­ратное,, находим, что первый и второй члены тождественны. Таким образом, получаем уравнения движения в виде

p^fl'=w5?fe-- (ад

Рассмотрим монохроматическую упругую волну в кристалле. Для этого мы должны искать решение уравнений движения в виде

щ = u_aie^l <^кг-^и'>

(и_т — постоянные), причем соотношение между волновым векто­ром к и частотой со должно быть определено так, чтобы написан­ная функция действительно удовлетворяла уравнению (23,1). Диф­ференцирование и| по времени приводит к умножению на—to, а дифференцирование по x_k — к умножению наi&_ft. Поэтому урав­нение (23,1) после подстановки превращается в

Написав u_t = 8_imu_m, переписываем это равенство в виде

(pco²6_im - l_ih[mk^i) и_т = 0. (23,2)

Это — система трех однородных уравнений первой степени отно­сительно неизвестных и_х, и_у, и_г. Как известно, такая система имеет отличные от нуля решения лишь при условии равенства нулю определителя коэффициентов уравнений

IWA-P»²L| = 0. (23,3)

Этим уравнением определяется зависимость частоты волны от> волнового вектора; об этой зависимости говорят как о законе дис­персии волн, а определяющее его уравнение называют дисперсион­ным. Уравнение (23,3) — третьей степени по о»². Оно имеет три, вообще говоря, различных корня со² = со| (к) — три, как гово­рят, ветви закона дисперсии. Подставляя поочередно каждый из этих корней обратно в уравнения (23,2) и решая их, мы найдем направления вектора смещения и в этих волнах, — как говорят, направления их поляризации (в силу своей однородности, урав­нения (23,2) не определяют, конечно, абсолютной величины век­тора и, остающейся произвольной) *). Направления поляризации трех волн с одним и тем же волновым вектором к взаимно перпен­дикулярны. Это важное утверждение следует прямо из того, что уравнение (23,3) можно рассматривать как уравнение, определяю­щее главные значения симметричного тензора второго pajHra ^ihimkkki ^[2]); уравнения же (23,2) определяют главные направле­ния этого тензора, которые, как известно, взаимно перпендику­лярны. Ни одно из этих направлений, однако, не является, вообще говоря, ни чисто продольным, ни чисто поперечным по отношению к направлению к.

Скорость распространения волны (ее групповая скорость) дается производной

U = -|£- (23,4)

(см. VI, § 67). В изотропной среде зависимость со (к) сводится к пропорциональности абсолютному значению k, и потому направ­ление этой скорости совпадает с направлением волнового вектора. В кристаллах это не так, и направление распространения волны не совпадает, вообще говоря, с направлением к. Векторы к и U кол-линеарны для некоторых исключительных направлений осей сим­метрии кристалла.

Из дисперсионного уравнения (23,3) видно, что в кристалле со является однородной функцией первого порядка от компонент век­тора к (если ввести в качестве неизвестной величины отношение ы/k, то коэффициенты уравнения не зависят от k). Поэтому ско­рость U — однородная функция нулевого порядка от k_x, k_y, k_z. Другими словами, скорость распространения волны, являясь функцией ее направления, не зависит от частоты.

^г) В изотропном теле этими ветвями являются со == cjfc (продольно поляри­зованные волны) и два совпадающих корня со == cjfe, отвечающие волнам с двумя независимыми поперечными направлениями поляризации,

Если построить в k-пространстве (т. е. в координатах k_x, k_yi k_z) поверхность постоянной частоты, to (k) = const (для какой-либо из ветвей закона дисперсии), то направление вектора (23,4) совпадает с нормалью к поверхности. Очевидно, что если эта по­верхность всюду выпуклая, то связь между направлениями U и к взаимно однозначна: каждому направлению к отвечает одно определенное направление U и наоборот. Если же поверхность постоянной частоты не всюду выпукла, то эта связь становится не взаимно однозначной: каждому направлению к по-прежнему

УПРУГИЕ ВОЛНЫ В КРИСТАЛЛАХ

отвечает (в данной ветви закона дисперсии) одно направление U, но заданное направление I) может осуществляться с различными направлениями к.

Задачи

1. Определить закон дисперсии упругих волн в кубическом кристалле,
распространяющихся а) в кристаллографической плоскости (001) (плоскость
грани куба); б) в кристаллографическом направлении [111] (направление диа-
гонали куба).

Решение. В кубическом кристалле отличны от нуля упругие модули Х_ХХхх = ^i, Х_хкуу ее Х₂, Х_хуху = Х₃ (и равные им компоненты тензора с заменой индексов х, у другими из х, у, г — см. § 10); оси х, у, г направлены вдоль ребер куба.

а) Выберем плоскость (001) в качестве плоскости х, у и пусть 6 — угол
между лежащим в ней волновым вектором к и осью х. Составив дисперсионное
уравнение (23,3) и решив его, найдем три ветви закона дисперсии:

рсо², ₂ = V^² + Ь₃ ± [(\ - hf~ ⁴ (*i + Ц (S - h - ²h)^sln2 9 cos²Qf'²}, рш² = X^k².

Волна третьей ветви поперечна и поляризована вдоль оси г. Волны первых двух ветвей поляризованы в плоскости х, у. Из соображений симметрии очевидно, что скорость распространения U = дшдк всех этих волн тоже лежит в плоско­сти х, у, поэтому для ее вычисления достаточно полученных выражений. При 6 = 0 (к вдоль оси х) имеем

рсо? = А,]£², pcof, = X,k²,

причем волна / продольна (поляризована вдоль оси х), а волна 2 поперечна (поляризована вдоль оси у).

При 0 = я/4 (к вдоль диагонали грани куба) имеем

pcof = V, (Ч + Х₂ + 2*₃) k\ pcol = V. (Xj - Х₂) k\

Волна 1 продольна, а волна 2 поперечна и поляризована в плоскости х, у.

б) В этом случае волновой вектор имеет компоненты k_x — k_y = k_z =
Решение дисперсионного уравнения дает

рш? = + 2Я₂ + 4Х₃),

Р»1,з = Vs^² (A-i — Х-2 + Х₃). Волна / продольна, волны 2 и 3 поперечны.

2. Определить закон дисперсии упругих волн в кристалле гексагональ-
ной системы.

Решение. Гексагональный кристалл имеет пять независимых упругих модулей (см. задачу 1 § 10), для которых введем обозначения:

Ххххх ⁼ ^"uvvv ^{= а}' ^хуху ⁼ ^> Х_ххуу = а 2Ь,

Xxxzz = X_yyzz — с, Х_хгхг = Xy_zyz — d, X_zzzz = f.

Ось z направлена по оси симметрии шестого порядка, направления же осей х, g могут быть выбраны произвольно. Выберем плоскость xz так, чтобы в ней лежал волновой вектор к. Тогда k_x = k sin 6, k_y == 0, k_z — k cos 9, где 9 — угол ме­жду к и осью z. Составляя уравнение (23,3) и решая его, найдем

рсо? = ft² (6 sin² 9-f-d cos² 9),

pcof,з = V26² {a sin² 6 + /cos² 9 + d ±

± [{(a- d) sin² 9 + (d - f) cos² 9)² + 4 (c +. df sin² 6 cos² б]¹'²}.

При в = 0 имеем

pco|_l2=fe4 pal = k^rf; волна 3 продольна, волны 1 и 2 поперечны.

§ 24. Поверхностные волны

Особым видом упругих волн являются волны, распространяю­щиеся вблизи поверхности среды и не проникающие в глубь нее — волны Рэлея (Rayieigh, 1885).

Напишем уравнения движения в виде (22,11—12)1

-|^-£²Лы=0 (24,1)

(где и — какая-либо из компонент векторов щ, щ, а с — соответ­ствующая ей скорость Ci или с_г), и будем искать решения, отве­чающие поверхностным волнам. Поверхность упругой среды будем предполагать плоской, и выберем ее в качестве плоскости х, у\ области среды пусть соответствуют z < 0.

Рассмотрим «плоскую» монохроматическую поверхностную волну, распространяющуюся вдоль оси х\ функция и {£, х, г) в ней имеет вад

где функция / (г) удовлетворяет уравнению /" = и²/; введено обо­значение

х = (&² - ©Ус²)'/*. (24,2)

Если к? — со²/с² < 0, то / (г) — периодическая функция, т. е. мы получили бы обычную плоскую волну, не исчезающую во всем объеме среды. Поэтому надо считать, что № — ъ>Ус² g> 0, и % — ве­щественное число. Уравнение имеет решения вида ехр (±хг); из них надо выбрать то, которое затухает при z~> — со.

Таким образам, мы приходим к следующему решению уравне­ний движения:

U = Const ё (к*-Ы)#а_ш (24,3)

Оно соответствует волне, быстро (экспоненциально) затухающей внутрь тела, т.е. распространяющейся только вблизи его поверх­ности. Величина к определяет скорость этого затухания.

Истинный вектор деформации и в волне является суммой Еекто-ров щ и щ, компоненты каждого из которых удовлетворяют урав­нению (24,1) со скоростью с = c_t для щ м с — c_t для щ. В случае объемных вола в неограниченной среде эти две части представляют собой две независимо распространяющиеся волны. В случае же поверхностных волн такое разделение на две независимые части оказывается (благодаря наличию граничных условий) невозмож­ным. Вектор смещения и должен быть определенной линейной комбинацией векторов щ и и_{. По поводу этих последних надо также отметить, что они отнюдь не имеют теперь наглядного смысла

i 24i

поверхностные волны

параллельных и перпендикулярных к направлению распростра­нения компонент смещения.

Для определения линейной комбинации векторов щ и щ, даю­щей истинное смещение и, надо обратиться к предельным условиям на границе тела. Отсюда же определится связь между волновым вектором к и частотой со, а следовательно, и скорость распростра­нения волны. На. свободной поверхности должно выполняться условие a_thn_h — 0. Поскольку вектор нормали п направлен по оси г, то отсюда следуют условия

О_хг = Oyt = O_zz = О,

откуда

= 0» и»* = 0, о (и_хх + и_т) -f (1 - а) u_zz = 0. (24,4)

Поскольку все величины не зависят от координаты y_t то второе из этих условий дает

„ _ ¹ (^диу. Л!кЛ — А.^диу — п ^и»^г ~ 2 \~дГ ду) ~ 2 ~Ы

С учетом (24,3) отсюда следует

а_и = 0. (24,5)

Таким образом, в поверхностной волне вектор деформации и ле­жит в плоскости, проведенной через направление распространения перпендикулярно к поверхности.

«Поперечная» часть волны щ должна удовлетворять условию (22,8) div щ = 0, или

дх ' дг

Ввиду (24,3) это условие приводит к равенству

iku_tx+ щи_и = 0, определяющему отношение u_tx!u_tz. Таким образом, имеем

^ut_x — ^Kt^{a е}^Р (ikx + x_tz — Ш),

«_(i =—i&a exp (ikx -\- щг — t©^)> (24,6)

где a — постоянная.

«Продольная» часть и_г удовлетворяет условию (22,9) rot и, = = 0, или

дщ_х дм(_г

= 0,

дг дх

откуда

iku_u — KiUtx = 0, к* = (k² — со²/с²)^1/2.
Таким образом, должно быть

щ_х = kbe^+^f-^, и_1г = —щЬ^^кх^\^г-^ш, (24,7)
где 6 — постоянная.

теперь воспользуемся первым и третьим из условий (24,4). выражая u_ih через производные от ы_г и вводя скорости с_г и Ct, переписываем эти условия в виде

ди_х, ди_г _ _n

Дата добавления: 2014-11-07