
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Усеченное нормальное распределение
|
|
|
|
Классическое нормальное распределение
Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым.
Считается, что наработка подчинена нормальному распределению (нормально распределена), если плотность распределения отказов (ПРО) описывается выражением:

| (1) |
где a и b – параметры распределения, соответственно, МО и СКО, которые по результатам испытаний принимаются:

где 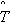 0,
0, 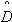 - оценки средней наработки и дисперсии.
- оценки средней наработки и дисперсии.
Графики изменения показателей безотказности при нормальном распределении приведены на рис. 1.
Выясним смысл параметров Т0 и S нормального распределения. Из графика f(t) видно, что Т0 является центром симметрии распределения, поскольку при изменении знака разности (t - T0) выражение (1) не меняется. При t = Т0 ПРО достигает своего максимума

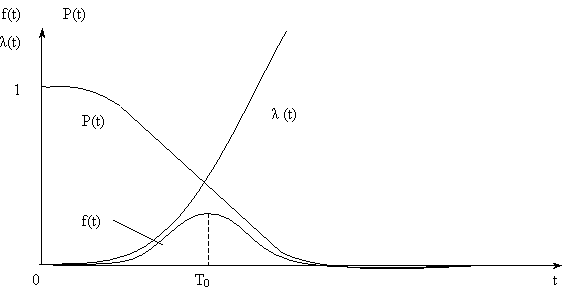
Рис.6.1
При сдвиге Т0 влево/вправо по оси абсцисс, кривая f(t) смещается в ту же сторону, не изменяя своей формы. Таким образом, Т0 является центром рассеивания случайной величины T, т. е. МО.
Параметр S характеризует форму кривой f(t), т. е. рассеивание случайной величины T. Кривая ПРО f(t) тем выше и острее, чем меньше S.
Изменение графиков P(t) и  (t) при различных СКО наработок (S1 < S2 < S3) и Т0 = const приведено на рис. 6.2.
(t) при различных СКО наработок (S1 < S2 < S3) и Т0 = const приведено на рис. 6.2.
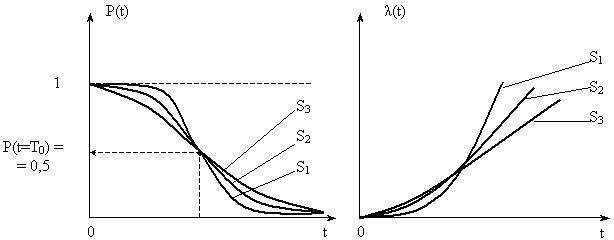
Рис. 6.2
Используя полученные ранее (главы 3, 4) соотношения между показателями надежности, можно было бы записать выражения для P(t); Q(t) и  (t) по известному выражению (1) для f(t). Не надо обладать богатой фантазией, чтобы представить громоздкость этих интегральных выражений, поэтому для практического расчета показателей надежности вычисление интегралов заменим использованием таблиц.
(t) по известному выражению (1) для f(t). Не надо обладать богатой фантазией, чтобы представить громоздкость этих интегральных выражений, поэтому для практического расчета показателей надежности вычисление интегралов заменим использованием таблиц.
С этой целью перейдем от случайной величины T к некоей случайной величине
|
|
|

| (2) |
распределенной нормально с параметрами, соответственно, МО и СКО M{X} = 0 и S{X} = 1 и плотностью распределения

| (3) |
Выражение (3) описывает плотность так называемого нормированного нормального распределения (рис. 6.3).
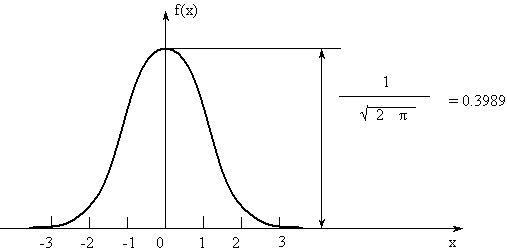
Рис. 6.3
Функция распределения случайной величины X запишется
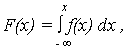
| (4) |
а из симметрии кривой f(x) относительно МО M{X} = 0, следует, что f(-x) = f(x), откуда F(-x) = 1 - F(x).
В справочной литературе приведены расчетные значения функций f(x) и F(x) для различных x = (t - Т0)/S.
Показатели безотказности объекта через табличные значения f(x) и F(x) определяются по выражениям:
| f(t) = f(x)/S; | (5) |
| Q(t) = F(x); | (6) |
| P(t) = 1 - F(x); | (7) |
 (t) = f(x)/S(1 - F(x)). (t) = f(x)/S(1 - F(x)).
| (8) |
В практических расчетах часто вместо функции F(x) пользуются функцией Лапласа, представляющей распределение положительных значений случайной величины X в виде:

| (9) |
Очевидно, что F(x) связана с  (x) следующим образом:
(x) следующим образом:
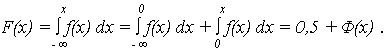
| (10) |
Как и всякая функция распределения, функция 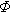 (x) обладает свойствами:
(x) обладает свойствами:
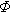 (x)(-
(x)(- 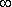 ) = -0,5;
) = -0,5; 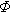 (x)(
(x)(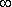 ) = 0,5;
) = 0,5; 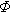 (x)(-x) = -
(x)(-x) = - 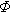 (x).
(x).
В литературе могут встретиться и другие выражения для 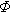 (x), поэтому, какой записью
(x), поэтому, какой записью 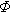 (x) пользоваться – это дело вкуса.
(x) пользоваться – это дело вкуса.
Показатели надежности объекта можно определить через 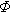 (x), используя выражения (5) – (8) и (10):
(x), используя выражения (5) – (8) и (10):
Q(t) = 0,5 + 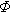 (x); (x);
| (11) |
P(t) = 0,5 - 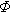 (x); (x);
| (12) |
 (t) = f(x)/S(0,5 - (t) = f(x)/S(0,5 - 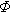 (x)). (x)).
| (13) |
Чаще всего при оценке надежности объекта приходится решать прямую задачу – при заданных параметрах Т0 и S нормально распределенной наработки до отказа определяется тот или иной показатель безотказности (например, ВБР) к интересующему значению наработки t.
Но в ходе проектных работ приходится решать и обратную задачу – определение наработки, требуемой по техническому заданию, ВБР объекта.
Для решения подобных задач используют квантили нормированного нормального распределения.
Квантиль – значение случайной величины, соответствующее заданной вероятности.
|
|
|
Обозначим:
tp – значение наработки, соответствующее ВБР P;
xp – значение случайной величины X, соответствующее вероятности P.
Тогда из уравнения связи x и t:

при x = xp; t = tp, получаем
tp= Т0 + xp S.
tp, xp – ненормированные и нормированные квантили нормального распределения, соответствующие вероятности P.
Значения квантилей xp приводятся в справочной литературе для P  0,5.
0,5.
При заданной вероятности P < 0,5 используется соотношение
xp = - x1-p.
Например, при P = 0,3
x0,3 = - x1- 0,3 = - x0, 7
Вероятность попадания случайной величины наработки T в заданный интервал [t1, t2] наработки определяется:
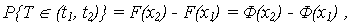
| (14) |
где x1 = (t1 - Т0)/S, x2 = (t2 - Т0)/S.
Отметим, что наработка до отказа всегда положительна, а кривая ПРО f(t), в общем случае, начинается от t = -  и распространяется до t =
и распространяется до t =  .
.
Это не является существенным недостатком, если Т0 >> S, поскольку по (14) нетрудно подсчитать, что вероятность попадания случайной величины T в интервал P{Т0 - 3S < T < Т0 + 3S} 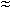 1,0 с точностью до 1%. А это означает, что все возможные значения (с погрешностью не выше 1%) нормально распределенной случайной величины с соотношением характеристик Т0 > 3S, находятся на участке Т0 ± 3S.
1,0 с точностью до 1%. А это означает, что все возможные значения (с погрешностью не выше 1%) нормально распределенной случайной величины с соотношением характеристик Т0 > 3S, находятся на участке Т0 ± 3S.
При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, 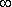 ) и используется усеченное нормальное распределение.
) и используется усеченное нормальное распределение.
Известно, что корректность использования классического нормального распределения наработки, достигается при Т0  3S.
3S.
При малых значениях Т0 и большом S, может возникать ситуация, когда ПРО f(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4).

Рис.6.4
Таким образом, нормальное распределение являясь общим случаем распределения случайной величины в диапазоне (- 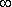 ;
; 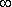 ), лишь в частности (при определенных условиях) может быть использовано для моделей надежности.
), лишь в частности (при определенных условиях) может быть использовано для моделей надежности.
Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений наработки до отказа.
В общем случае усечение может быть:
· левым – (0;  );
);
· двусторонним – (t1 , t2).
Смысл усеченного нормального распределения (УНР) рассмотрен для случая ограничения случайной величины наработки интервалом (t1 , t2).
|
|
|
Плотность УНР 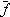 (t) = c f(t),
(t) = c f(t),
где
c – нормирующий множитель, определяемый из условия, что площадь под кривой 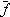 (t) равна 1, т. е.
(t) равна 1, т. е.

Откуда
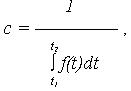
где
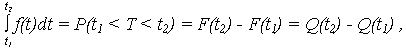
Применяя переход от случайной величины Т = {t} к величине X = {x}:
x2 = (t2 – Т0)/S; x1 = (t1 – Т0)/S,
получается

поэтому нормирующий множитель c равен:

Поскольку [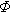 (x) (x2) -
(x) (x2) - 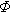 (x) (x1)] < 1, то c > 1, поэтому
(x) (x1)] < 1, то c > 1, поэтому 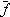 (t) > f(t). Кривая
(t) > f(t). Кривая 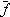 (t) выше, чем f(t), т. к. площади под кривыми
(t) выше, чем f(t), т. к. площади под кривыми 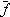 (t) и f(t) одинаковы и равны 1 (рис. 5).
(t) и f(t) одинаковы и равны 1 (рис. 5).

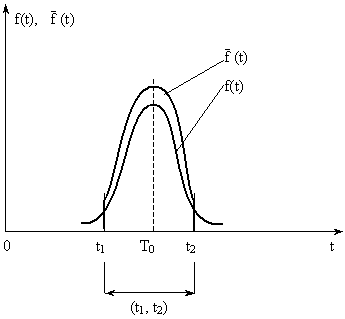
Рис. 6.5
Показатели безотказности для УНР в диапазоне (t1 , t2):

УНР для положительной наработки до отказа – диапазон (0; 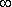 ) имеет ПРО
) имеет ПРО
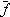 (t) = c0 f(t),
(t) = c0 f(t),
где c0 – нормирующий множитель определяется из условия:
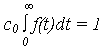
и равен (аналогично предыдущему):
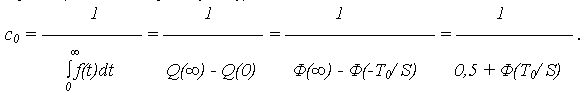
Показатели безотказности УНР (0;  )
)

Изменение нормирующего множителя c0 в зависимости от отношения Т0 /S приведено на рис. 6.
 Рис. 6.6.
Рис. 6.6.
При Т0 = S, Т0 / S = 1 c0 = max ( 1,2).
1,2).
При Т0 / S  2,5 c0 = 1,0, т.е.
2,5 c0 = 1,0, т.е.  (t)(t) = f(t).
(t)(t) = f(t).
Контрольные вопросы и задачи:
1. Объясните почему распределение Гаусса называется нормальным?
2. Поясните на изменении кривой плотности распределения отказов влияние параметров распределения: матожидания и дисперсии?
3. Приведите расчетные выражения для показателей безотказности, определенные через табличные функции: f(x), F(x) и 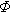 (x)?
(x)?
4. При каких условиях корректно использовать классическое нормальное распределение, и в каких случаях целесообразно применять усеченные нормальные распределения?
5. Приведите расчетные выражения показателей безотказности для усеченного «слева» нормального распределения?
6. Наработка до отказа серийно выпускаемой детали распределена нормально с параметрами: Т0 = M(T) = 104 час, S = S (T) = 250 час. Определить:
1) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [ 5000, 9000 час];
2) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [ Т0 - 3S, Т0 + 3S ];
3) вероятность того, что безотказно проработав до момента времени 5000 час, деталь безотказно проработает и до 9000 час?
Ответы: 1) 0.00003, 2) 0.9974, 3) 0.99997.
|
|
|
7. Комплектующая деталь, используемая при изготовлении устройства, по данным поставщика этой детали имеет нормальное распределение наработки с параметрами:
Т0 = 4 · 103 час, S = 800 час. Определить интересующую конструктора прибора:
1) наработку до отказа, соответствующую 90% надежности детали;
2) вероятность того, что при монтаже деталь имеет наработку, лежащую в интервале [ 2.5 · 103, 3 · 103 ];
3) вероятность того, что при монтаже деталь имеет наработку, большую, чем 2.5 103 час?
Ответы: 1) 2974.4, 2) 0.0755, 3) 0.9699.
Глава 7.ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НАРАБОТКИ ДО ОТКАЗА: ЭКСПОНЕНЦИАЛЬНЫЙ, ЛОГНОРМАЛЬНЫЙ И ГАММА-РАСПРЕДЕЛЕНИЕ
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 908; Нарушение авторских прав?; Мы поможем в написании вашей работы!