
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Чудові границі
|
|
|
|
Озн.5 Точка розриву функції наз. точкою розриву 1 роду, якщо ф-я має скінченні границі зліва та справа.
Класифікація точок розриву функції
Якщо т. x0 належить обл.. визначення ф-ії, або її межі і не є точкою неперервності то кажуть, що x0 - точка розриву ф-ії. Це можливо в слідуючи випадках:
1) в т. x0 ф-ія не визначена
2)не існує границя ф-ії при x x0
x0
3)границя існує, але вона не дорівнює значенню ф-ії в т.x0.
lim f(x) = f (x0-0); lim f(x)= f (x0+0)

 0
0  0
0
 Озн.6 Якщо границя зліва і справа скінченні числа, маємо стрибок.
Озн.6 Якщо границя зліва і справа скінченні числа, маємо стрибок.
Озн.7 Точка x0 розриву першого роду, в якій f (x-0)=f (x+0)  f(x) наз. точкою усуненого розриву.
f(x) наз. точкою усуненого розриву.

 Озн.8 Якщо ф-я на відрізку [a,b] має лише скінченне число точок розриву 1 роду, то її наз. кусочно-неперервною.
Озн.8 Якщо ф-я на відрізку [a,b] має лише скінченне число точок розриву 1 роду, то її наз. кусочно-неперервною.
Озн.9 Якщо хоча б одна границя справа або зліва дорівнює нескінченності маємо розрив 2 роду.
 розрив 2 роду
розрив 2 роду 
1.Перша чудова границя
lim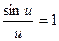 або lim
або lim 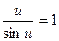


Доведення
Розгл. дугу кола радіуса R=1, з центральним кутом х (0<x< /2) ОА =1 sin x = MK; tg x = AT(1)
/2) ОА =1 sin x = MK; tg x = AT(1)




 М Т S
М Т S OAM < ScekOAM<S
OAM < ScekOAM<S OAT.
OAT.
 х 1/2OA . MK<1/2 OA . AM<1/2OA . AT. Використаємо
х 1/2OA . MK<1/2 OA . AM<1/2OA . AT. Використаємо
 О К А рів-я (1) 1/2 sin x< 1/2 x<1/2tg x => sinx<x<tgx/sinx (2)
О К А рів-я (1) 1/2 sin x< 1/2 x<1/2tg x => sinx<x<tgx/sinx (2)
1> >cos
>cos 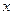
0<1- <1-cos x, т.я.sin x/2 <1 то sin2 x/2< sin x/2 враховуючи (2)
<1-cos x, т.я.sin x/2 <1 то sin2 x/2< sin x/2 враховуючи (2) 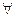 х, яке належить (0,
х, яке належить (0,  ) маємо 1-соs x - 2sin2 x/2< 2 sin x/2<2 . x/2
) маємо 1-соs x - 2sin2 x/2< 2 sin x/2<2 . x/2
т.ч. 0<1- <x, візьмемо
<x, візьмемо  >0,
>0,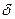 = min{
= min{ ,
, } =>
} =>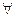 x
x 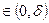 ,виконаємо перевірку х<
,виконаємо перевірку х< => 0<1-
=> 0<1- =>
=>  => 1=
=> 1= 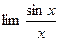 -до тогож
-до тогож
 - парна => ліва границя
- парна => ліва границя  в т.х=0=1
в т.х=0=1  0
0
ð  lim
lim 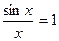 .
.
Приклад. 

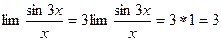


2.Друга чудова границя.
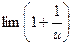 u =
u = 1/ u = e
1/ u = e
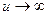

Доведення.
Раніше доведимо, що lim (1+ ) n = e, доведимо, що lim (1+
) n = e, доведимо, що lim (1+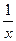 ) x = e.
) x = e.

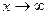
Нехай х>1;n=[x]=> x = n +  де n
де n  N,
N, 
 [0;1)Т.я. n
[0;1)Т.я. n  x<n+1
x<n+1  то
то  n <
n < 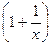 x <
x <  n +1 при х
n +1 при х (n
(n )
)
lim (1+ ) n+1 = lim
) n+1 = lim  n lim
n lim  = e
= e  1=e
1=e



lim  n =
n =  =
=  = e => lim
= e => lim 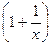 x = e.
x = e.
Розгл. х<-1, нахай х = -у, => 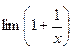 x =
x = 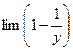 -y =
-y = 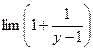 y =
y =
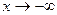
 y
y
= 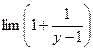 y-1
y-1 
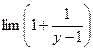 =e . 1 =e при х
=e . 1 =e при х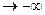



Приклад.
lim  x / 2 = e
x / 2 = e
x
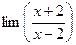 x =lim
x =lim 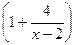 (x-2) / 4* (4/ (x-2)) * x = e lim 4x / x-2 =e4
(x-2) / 4* (4/ (x-2)) * x = e lim 4x / x-2 =e4
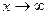

§ 8. ПОХІДНА ФУНКЦІЯ
 Нехай задана функція f (х). Розглянемо 2 значення аргум. х0 і х
Нехай задана функція f (х). Розглянемо 2 значення аргум. х0 і х
|
|
|
y Δх = х – х0 ; Δy = y – y0 = f (x) – f(x0)
 y0 т. ч. x = x0 + Δx
y0 т. ч. x = x0 + Δx
Δx Озн 1 Похідною y = f (x) в т. x0 наз. границя відношен-
0 x0 x ня приросту ф – ції Δy в цій точці, до приросту
аргумента Δx, якщо x→ 0
f ' (x) = 
 Нехай на кривій задана т. М0
Нехай на кривій задана т. М0
 M Озн.2 Дотичною є пряма, яка займає
M Озн.2 Дотичною є пряма, яка займає
граничне положення січної.
М0 Δ У
У0
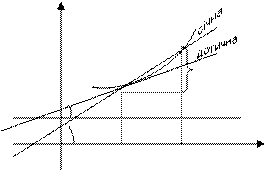
α Розглянемо графік y = f(x), яка має в
β т. М0 (x0,y0) невертикальну дотичну.
0 х0 х0+х Знайдемо кутовий коефіцієнт.
k = tg α, для цього проведемо через
т. М0 січну М0М де М(x0+ ∆x; y0+∆y).
Її кутовий коефіцієнт kсіч = tg β =  , при
, при  ,
, 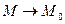 при цьому січна необмежено наближається до дотичної, тобто
при цьому січна необмежено наближається до дотичної, тобто 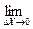 β = α, а тому
β = α, а тому 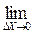 tg β = tg α
tg β = tg α 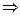 кутовий коефіцієнт дотичної:
кутовий коефіцієнт дотичної:
k = tg α = 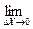 tg β =
tg β = 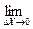
 = y′ = f ′ (x0)
= y′ = f ′ (x0)
Висновок Кутовий коефіцієнт дотичної до графіка функції в точці з
абсцисою Х0 дорівнює значенню похідної цієї функції в т. x0
k = f ′ (x0)
 |
Озн. 3 Якщо f(x) має неперервну похідну f ′ (x) на [а,b], то ф-ція f(x) наз.
гладкою на цьому проміжку.
 Озн. 4 Функція f (х) похідна якої f ′ (х) допускає тільки скінчене число
Озн. 4 Функція f (х) похідна якої f ′ (х) допускає тільки скінчене число
точок розриву, причому I роду, на даному проміжку [а,b],
наз. кусочно – гладкою на цьому проміжку.
Зауваження Знаходження похідної ф – ції наз. диференціюванням
Теорема Якщо ф – ція диференційована, в будь якій точці то вона не-
перервна у ній.
§ 9. ПРАВИЛА ДІФЕРЕНЦІЮВАННЯ ФУНКЦІЙ
Теорема 1 Якщо ф – ції u = u (x) та v = v (x), диференційовані в даній
точці х
То в цій же точці диференційована і їх сума, до того ж:
(u + v)' = u' + v'
Доведення Розглянемо ф – цію y = f (x) = u (x) + v (x), приросту Δх
відповідає приріст
Δy = f (x + Δx) – f (x) = u (x + Δx) + v (x + Δx) – u (x) – v (x)
= (u (x + Δx) – u (x)) + (v (x +Δx) – v (x)) = Δu = Δv
Тоді y' = 
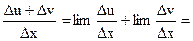 u' + v'
u' + v'
Зауваження: аналогічно (u – v)' = u' - v'
Теорема 2 Якщо ф – ції u = u (x) та v = v (x), диференційовані на проміжку
(a, b), то
(u *v)' = u' v + uv'
Доведення Якщо x – отримує приріст Δx, то ф – ції y = u * v отримують
|
|
|
Відповідно Δy, Δu, Δv, причому
Δy = (u+Δu) * (v+Δv) – uv = Δuv + uΔv +ΔuΔv, тоді 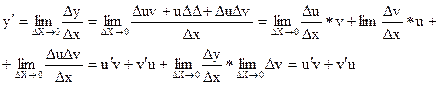
Наслідок (c*u)'= c*u'
Теорема 3 Якщо в даній точці x ф – ції u = u (x) та v = v (x) диф – ні
та v (x) ≠ 0, то в цій точці диф – на і частка

Доведення Нехай Δx – приріст, а Δu та Δv – відповідний приріст
ф – цій тоді y = u/v отримає приріст
 тоді
тоді

 0
0
Похідна складної ф – ції
Теорема 4 Нехай y = q (x), x є (a, b) має похідну в т. x0 є (a, b), а
z = φ (y) має похідну в т. y0 = q (x0). Тоді z (х) = φ (q (x))
має похідну в т. x0 до того ж
z' (x0) = φ' (y0) * q (x0)
Доведення z = φ (q (x)) має похідну => 

 Похідна оберненої, неявної ф – ції та ф – ції заданої параметрично
Похідна оберненої, неявної ф – ції та ф – ції заданої параметрично
Теорема 5 Якщо для ф – ції y = f (x) існує обернена ф – ція x = φ (y), яка
в розглядуваній точці у' має похідну φ' (у), відмінну від нуля,
то в відповідній т. x ф – ція у = f (х) має похідну f ' (x) рівну

 тобто f ' (x) =
тобто f ' (x) = 
 Доведення Візьмемо приріст Δy тоді Δx = φ (у + Δу) – φ (у) так як
Доведення Візьмемо приріст Δy тоді Δx = φ (у + Δу) – φ (у) так як
f (х) монотонна то,
Δx ≠ 0 → 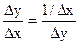 так як φ (у) неперервна,
так як φ (у) неперервна,
то Δx → 0 при Δy→ 0. Тоді 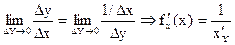 ч. т. д.
ч. т. д.
Нехай ф – ція задана параметричними рівняннями х = х (t) – існують
y = у (t)
в околі т. t, при чому х' (t) ≠ 0, тоді
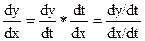 , тобто y' (х) =
, тобто y' (х) = 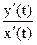
Нехай ф – ція задана рівнянням F (х, у) = 0, а не у = f (х), тобто неявно. Для того, щоб знайти похідну треба про диференціювати обидві частини цього рівняння по х і з отриманого р – ня знайти у ' (х).
Приклад х2 – ln y – x2 ey = 0 (x tgx)
Таблиця похідних
Для U = U (x) виконується:
c'=0
x' = 1
(u n)' = u' nun-1
(аu) = au u' ln a
(eu)' = eu u'
(sin u)' = u' cos u
(cos u)' = u' sin u
(tg u) ' = 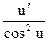
(ctg u) ' = 
(arcsin u) ' = 
(arcos u) ' = 
(arctg u) ' = 
(sh u)' = u' ch u
(ch u)' = u' sh u
(ln u) ' = 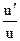
(loga u) ' = 
§ 10. РІВНЯННЯ ДОТИЧНОЇ ТА НОРМАЛІ ДО КРИВОЇ
Розглянемо криву y = f (x). На цій лінії візьмемо т. М0 (х0. у0)
 |
yo
Q)α P (R
0 xo
 |
Запишемо р – ня дотичної, що проходить через т. М0 і не║осі ОУ.
Рівняння прямої з даним кутовим коефіцієнтом ″К″ що проходить через т. М0 (х0, у0) має вигляд:
у - у0 = К (х – х0); К = f ' (x0) =>
=> y - y0 = f ' (x0) * (х – х0)
Озн. 1 Нормаллю до кривої в даній точці наз. пряма, що проходить через
цю точку перпендикулярна до дотичної.

Довжина відрізку QM0 дотичной називається довжиною дотичної. Проекція цього відрізку на вісь ОХ QP називається під дотичною. Довжина М0R називається довжиною нормалі, а проекція RP – називається під нормаллю.
|
|
|
 § 11. ПОХІДНІ ВИЩИХ ПОРЯДКІВ
§ 11. ПОХІДНІ ВИЩИХ ПОРЯДКІВ
Озн. 1 Якщо функція має першу похідну, то похідна від похідної
першого порядку наз. похідною другого порядку, або другою
похідною.
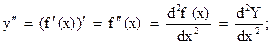 аналогічно
аналогічно

Похідна позначається римськими цифрами: IV, V … або (n – 1), (n) фізичний зміст похідної другого порядку:
 - прискорення прямолінійного руху за час t.
- прискорення прямолінійного руху за час t.
Друга похідна ф – ції заданої параметрично:
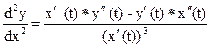
§ 12. ПОНЯТТЯ ДИФЕРЕНЦІАЛУ
Якщо ф – ція y = f (х) диференційована на [a. b], то  відповідно до властивості границі і нескінченно малої.
відповідно до властивості границі і нескінченно малої.
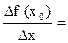 f ' (x0) + α (Δx), де α (Δx) → 0 коли Δx→ 0, тоді Δf (x0) = f ' (x0) Δx + α (Δx) Δx
f ' (x0) + α (Δx), де α (Δx) → 0 коли Δx→ 0, тоді Δf (x0) = f ' (x0) Δx + α (Δx) Δx
 |
Озн. 1 Якщо функція f (х) має в точці х0 похідну f ' (x0), тоді добуток
f ' (x0) Δх наз. диференціалом ф – ції f (x) в т. x0 і записують df (x0) = f ' (x0) Δx.
T. я. dx = x ' Δx = 1 *Δx тобто dx ≈ Δx
маємо df (x) = f ' (x) dx
Усі формули похідної працюють для диф – ла, як і властивості.
Геометричний зміст диф – лу
 |
f(x0+Δx) N
Δу K
 f (x0) м)α O
f (x0) м)α O
Δx
0 x0 x0+Δx
МК – дотична
З ΔМКО маєм КО = МО * tg
Але МО = Δх, tg = f ' (x0)
т. ч. КО = f ' (x0) * Δx = dy
Т. ч. Диф – ал ф – ції y = f (x)
в т. x0 дорівнює приросту
ординати дотичної.
dy ≠ Δy KO ≠ N, але при малих
Δх, Δу ≈ dy
Застосування диференціалу до наближених обчислень
Δу = f ' (x)Δx => f (x+Δx) – f (x) = f ' (x)Δx
f (x+Δx) = f (x) + f ' (x)Δx
 Озн. 2 Абсолютною похибкою Δо наближеної величини x наз. модуль
Озн. 2 Абсолютною похибкою Δо наближеної величини x наз. модуль
різниці між її точним значенням "а" та наближеним
Δо = 
 Озн. 3 Відносною похибкою δ називають: δ =
Озн. 3 Відносною похибкою δ називають: δ = 
Диференціали вищих порядків
 Озн. 4 Диф – ал від диф – ла першого порядку називають диф – лом
Озн. 4 Диф – ал від диф – ла першого порядку називають диф – лом
другого порядку
d2y = d (dy) d2y = f '' (x) dx2
Аналогічно знаходимо диф – ал 3 го та 4 го порядку.
d n y = d (d n-1 y) = f (n) (x) dx n
Зауваження Теореми про добуток і частку похідної справедливі і
для диф – лу d (uv) = duv + dvdu
d 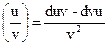 , але для диф – лу (n > 1) порядку вони
, але для диф – лу (n > 1) порядку вони
мають зміст тільки коли х незалежна змінна.
(Тобто для складної ф – ції ці формули не виконуються)
d2y = d (dy) = d (φ' (z)dz) = dz d (φ' (z)) + φ' (z) d (dz) = dz φ'' (zdz + φ' (z)) d2z = φ'' (x)dz2 = φ' (z)d2 z.
|
|
|
§ 13. ДЕЯКІ ТЕОРЕМИ ПРО ДИФЕРЕНЦІЙОВАНІ Ф – ЦІЇ.
ПРАВИЛО ЛОПІТАЛЯ
Теорема Ферма (Фр. 1601 – 1665)
 Нехай функція y = f (x) визначена на інтервалі (a, b) і приймає в деякій
Нехай функція y = f (x) визначена на інтервалі (a, b) і приймає в деякій
Точці x = c є (a, b) найбільше або найменше значення. Тоді якщо в т.
x = c існує похідна цієї ф – ції, вона дорівнює нулю.

y
c Х
0 a в
Довед. Нехай в т. c ф – ція приймає найбільше значення f (c) = М, на ін-тервалі (a, b) Покажемо що f ' (c)=0
Так як f ' (c) = 
т. я. в т. c значення найбільше =>
f (c) ≥ f (c + Δx) i f (c +Δx) – f (c) ≤ 0 =>
Глава 1
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1461; Нарушение авторских прав?; Мы поможем в написании вашей работы!