
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дискретные случайные величины
|
|
|
|
Случайные величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначения:
X, Y, Z – случайные величины;
x, y, z – их возможные значения.
Если случайная величина Х имеет три возможных значения, то они обозначаются: х 1, х 2, х 3.
Запись Х = х 1 – это событие, состоящее в том, что случайная величина Х примет возможное значение х 1.
(ДСВ)
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений ДСВ может быть конечным или бесконечным.
Задать ДСВ можно с помощью закона распределения
Законом распределения ДСВ называют соответствие между возможными значениями и их вероятностями.
Этот закон можно задать таблично, аналитически и графически.
а) Табличный:
Х х 1 х 2 … хп – возможные значения
Р р 1 р 2… рп – их вероятности.
Так как в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события Х = х 1, Х = х 2,…, Х = хп образуют полную группу, т.е. сумма вероятностей равна 1:
р 1 + р 2 +…+ рп = 1.
Если множество возможных значений Х бесконечно (счётно), то ряд р 1 + р 2 + … сходится и его сумма равна 1.
Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрыш – 50 рублей и 10 выигрышей по 1 рублю. Найти закон распределения ДСВ Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
□
Возможные значения ДСВ Х: х 1 = 50, х 2 = 1, х 3 = 0.
Вероятности этих возможных значений: р 1 = 0,01, р 2 = 0,1, р 3 = 0,89.
|
|
|
Искомый закон распределения:
Х 50 1 0
Р 0,01 0,1 0,89
К о н т р о л ь:
0,01 + 0,1 + 0,89 = 1.
■
б) Графический.
Для наглядности закон распределения ДСВ можно изобразить графически. Для этого в прямоугольной системе координат строят точки (хi; рi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения
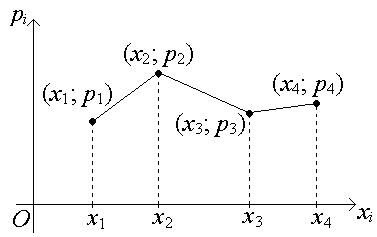
в) Аналитический.
При аналитическом задании закона распределения дается формула вычисления вероятностей возможных значений ДСВ.
1. Биномиальное распределение.
Пусть выполняется схема Бернулли. Рассмотрим в качестве ДСВ Х – число появлений события А в п независимых испытаниях.
Событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо п раз. То есть возможные значения ДСВ Х: х 1=0, х 2= 1,…, хп +1= п. Для определения вероятностей этих возможных значений используется формула Бернулли:
Рп (k) = 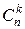 pkqn−k, (1)
pkqn−k, (1)
где k = 0, 1, 2, …, п.
Формула (1) – аналитическое выражение искомого закона распределения.
Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван “биномиальным” потому, что правую часть формулы (1) можно рассматривать как общий член разложения бинома Ньютона:
(р + q) n = 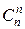 pn +
pn + 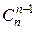 pn −1 q + … +
pn −1 q + … + 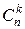 pkqn−k + … +
pkqn−k + … + 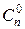 qn.
qn.
Пример. Монета брошена два раза. Написать в виде таблицы закон распределения ДСВ Х – числа выпадения “орла”.
□
Вероятность появления “орла” в каждом бросании монеты р = 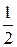 . Следовательно, вероятность не появления “орла” q = 1 − р =
. Следовательно, вероятность не появления “орла” q = 1 − р = 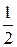 .
.
При двух бросаниях “орёл” может появиться либо 0 раз, либо 1 раз, либо 2 раза. Таким образом, возможные значения Х: х 1 = 0, х 2 = 1, х 3 = 2.
Вероятности этих возможных значений найдем по формуле Бернулли:
Р 2(0) = 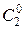 q 2 =
q 2 = 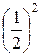 =
= 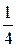 = 0,25;
= 0,25;
Р 2(1) = 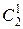 рq = 2∙
рq = 2∙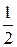 ∙
∙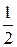 =
= 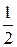 = 0,5;
= 0,5;
Р 2(2) = 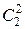 р 2 =
р 2 = 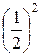 =
= 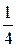 = 0,25.
= 0,25.
Искомый закон распределения:
Х 0 1 2
Р 0,25 0,5 0,25
К о н т р о л ь:
0,25 + 0,5 + 0,25 = 1.
■
2. Распределение Пуассона.
|
|
|
Если число независимых испытаний п велико, а вероятность события А р ≤ 0,1, то вычислять вероятности возможных значений ДСВ Х можно по формуле Пуассона:
Рп (k) 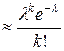 , где λ = пр. (2)
, где λ = пр. (2)
Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.
Пример. □ Поступление вызовов на АТС, на пункт неотложной медицинской помощи и т.д. ■
Потоки могут обладать свойствами стационарности, отсутствия последействия, ординарности.
Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала отсчёта; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени (1; 7), (10; 16), (Т; Т + 6) одинаковой длительности t = 6 единиц времени равны между собой.
Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. То есть, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.
Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью появления только одного события.
Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.
Замечание. Если поток событий представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный поток (при условии его ординарности) близок к простейшему.
Интенсивностью потока λ называют среднее число событий, которые появляются в единицу времени.
Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона
|
|
|
Рt (k) 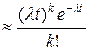 .
.
Таким образом, формулу Пуассона можно считать математической моделью простейшего потока событий.
Пример. Среднее числа вызовов поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит: а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.
□
По условию, λ = 2, t = 5, k = 2. По формуле Пуассона
Рt (k) 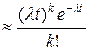 :
:
а) вероятность того, что за 5 минут поступит 2 вызова,
Р 5(2)  ≈
≈  = 0,00225.
= 0,00225.
Это событие практически невозможно.
б) События “не поступило ни одного вызова” и “поступил один вызов” несовместны, поэтому по теореме сложения искомая вероятность того, что за 5 минут поступит менее двух вызовов, равна
Р 5(k < 2) = Р 5(0) + Р 5(1) = e −10 + 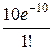 = 0,000495.
= 0,000495.
Это событие практически невозможно.
в) События “поступило менее двух вызовов” и “поступило не менее двух вызовов” противоположные, поэтому искомая вероятность того, что за 5 минут поступит не менее двух вызовов
Р 5(k ≥ 2) = 1 − Р 5(k < 2) = 1 − 0,000495 = 0,999505.
Это событие практически достоверно.
■
3. Геометрическое распределение.
Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0 < p < 1) и, следовательно, вероятность его не появления q = 1 − р. Испытания заканчиваются, как только появится событие А.
Пусть ДСВ Х - число испытаний до первого появления события А. Возможные значения Х: х 1 = 1, х 2 = 1,….
Пусть в первые k − 1 испытаниях событие А не появилось, а в k -ом испытании наступило. Вероятность такого события по теореме умножения вероятностей независимых
Р (Х = k) = qk − 1 p, (3)
где k = 1, 2,….
Распределение (3) носит название геометрическое, т.к. подставляя в (3) k = 1, 2,…., получаем геометрическую прогрессию с первым членом р и знаменателем q (0 < q < 1)
p, qp, q 2 p, …, qk − 1 p,….
Пример. Из орудия производится стрельба по цели до 1-го попадания. Вероятность попадания в цель p = 0,6. Найти вероятность того, что попадание произойдет при 3-м выстреле.
|
|
|
□
По условию, р = 0,6, q = 0,4, k = 3. Искомая вероятность по формуле (3):
Р (Х = 3) = qk − 1 p = 0,42∙0,6 = 0,096.
■
4. Гипергеометрическое распределение.
Пусть в партии из N изделий имеется М стандартных (М < N). Из партии случайно отбирают п изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причём отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима).
Случайная величина Х – число т стандартных изделий среди п отобранных.
Возможные значения Х: 0, 1, 2,…, min (M, n).
Найдём вероятность того, что Х = т, т.е. среди п отобранных изделий ровно т стандартных. Используем для этого классическое определение вероятности.
Общее число возможных элементарных исходов − 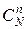 .
.
Число исходов, благоприятствующих событию Х = т (среди п изделий ровно т стандартных) − 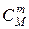
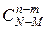 .
.
Искомая вероятность:
Р (Х = т) = 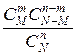 . (4)
. (4)
Формула (4) определяет распределение вероятностей, которое называют гипергеометрическим.
Числовые характеристики ДСВ
Математическое ожидание.
Математическим ожиданием ДСВ Х называют сумму произведений всех её возможных значений х 1, х 2, …, хп на их вероятности р 1, р 2,…, рп:
М (Х) = х 1 р 1 + х 2 р 2 + … + хп рп.
Если ДСВ Х принимает счетное множество возможных значений, то
М (Х) = 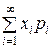 ,
,
причём математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Пример. Найти М (Х), зная закон распределения ДСВ Х:
Х 3 5 2
Р 0,1 0,6 0,3.
□
М (Х) = х 1 р 1 + х 2 р 2 + х 3 р 3 = 3∙0,1+ 5∙0,6 + 2∙0,3 = 3,9.
■
Пример. Найти математическое ожидание числа появления события А в одном испытании, если вероятность события А равна р.
□
ДСВ Х – число появлений события А в одном испытании может принимать только два значения: х 1 = 1 (событие А наступило) с вероятностью р и х 2 = 0 (событие А не наступило) с вероятностью q = 1 – p.
Следовательно,
М (Х) = 1∙ р + 0∙ q = p.
Итак, математическое ожидание числа появления события А в одном испытании равно вероятности этого события.
■
Пусть произведено п испытаний, в которых ДСВ Х приняла т 1 раз значение х 1, т 2 раз значение х 2, …, тk раз значение хk, причём т 1 + т 2 + …+ + тk = п. Тогда сумма всех значений, принятых Х:
х 1 т 1 + х 2 т 2 + …+ хk тk.
Найдём среднее арифметическое 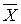 всех значений:
всех значений:
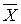 =
= 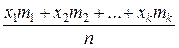
или
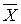 = х 1
= х 1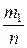 + х 2
+ х 2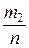 + … + хk
+ … + хk 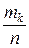 .
.
Так как 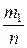 − относительная частота w 1 значения х 1;
− относительная частота w 1 значения х 1; 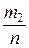 − относительная частота w 2 значения х 2 и т.д., то
− относительная частота w 2 значения х 2 и т.д., то
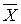 = х 1 w 1 + х 2 w 2 + … + хk wk.
= х 1 w 1 + х 2 w 2 + … + хk wk.
Допустим, что число испытаний велико, тогда
w 1 ≈ р 1, w 2 ≈ р 2, …, wk ≈ рk.
Следовательно,
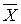 ≈ х 1 р 1 + х 2 р 2 +…+ хk рk
≈ х 1 р 1 + х 2 р 2 +…+ хk рk
или
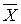 ≈ М (Х).
≈ М (Х).
Вероятностный смысл полученного результата: математическое ожидание приближённо равно (тем точнее, чем больше п) среднему арифметическому наблюдаемых значений случайной величины.
Замечание. Математическое ожидание всегда больше наименьшего и меньше наибольшего из возможных значений. В этом смысле оно характеризует расположение распределения и поэтому его часто называют центром распределения.
Свойства математического ожидания
10. Математическое ожидание постоянной величины равно этой постоянной:
М (С) = С.
20. Постоянный множитель можно выносить за знак математического ожидания:
М (СХ) = С ∙ М (Х).
30. Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
М (ХY) = М (Х)∙ М (Y).
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Пример. Пусть Х, Y – независимые случайные величины с законами распределения:
Х 5 2 4 Y 7 9
Р 0,6 0,1 0,3, Р 0,8 0,2.
Найти М (ХY).
□
Имеем
М (Х) = 5∙0,6+ 2∙0,1 + 4∙0,3 = 4,4;
М (Y) = 7∙0,8+ 9∙0,2 = 7,4.
Так как Х, Y – независимые случайные величины, то
М (ХY) = М (Х)∙ М (Y) = 4,4∙7,4 = 32,56.
■
40. (Справедливо для независимых и зависимых случайных величин).
Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
М (Х + Y) = М (Х) + М (Y).
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
□
Пусть
Х – число очков, которые могут выпасть на 1-ой кости;
Y – число очков, которые могут выпасть на 2-ой кости.
Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5, 6, причём вероятность каждого из этих значений равна 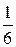 .
.
Найдём математическое ожидание числа очков, которые могут выпасть на 1-ой кости:
М (Х) = 1∙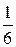 + 2∙
+ 2∙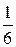 + 3∙
+ 3∙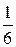 + 4∙
+ 4∙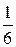 + 5∙
+ 5∙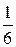 + 6∙
+ 6∙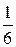 =
= 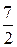 .
.
Очевидно, что и М (Y) = 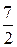 .
.
Искомое математическое ожидание:
М (Х + Y) = М (Х) + М (Y) = 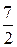 +
+ 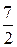 = 7.
= 7.
■
Теорема. Математическое ожидание числа появлений события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
М (Х) = пр.
Пример. Вероятность попадания в цель при стрельбе из орудия р = 0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.
□
Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание:
М (Х) = пр = 10∙0,6 = 6 (попаданий).
■
Дисперсия.
Пусть Х – случайная величина, М (Х) – её математическое ожидание. Рассмотрим новую случайную величину:
Х – М (Х).
Отклонением называют разность между случайной величиной и её математическим ожиданием, т.е. Х – М (Х) − отклонение.
Закон распределения отклонения:
Х – М (Х) х 1 – М (Х) х 2 – М (Х) … хk – М (Х)
P p 1 p 2 pk
Теорема 1. Математическое ожидание отклонения равно нулю.
○ Из свойств математического ожидания и того, что М (Х) = const, имеем
М [ Х – М (Х)] = М (Х) − M [ М (Х)] = М (Х) − М (Х) = 0. ●
Замечание. Наряду с термином “отклонение” используют термин “центрированная величина” и обозначают
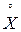 = Х – М (Х).
= Х – М (Х).
Такое название связано с тем, что математическое ожидание есть центр распределения.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг её среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
Дисперсией (рассеянием) ДСВ Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D (X) = М [ Х – М (Х)]2. (1)
Пример. Найти D (X), если Х задана законом распределения
Х 1 2 5
Р 0,3 0,5 0,2.
□
Найдем М (Х):
М (Х) = 1∙0,3 + 2∙0,5 + 5∙0,2 = 2,3.
Найдем все возможные значения квадрата отклонения:
[ х 1– М (Х)]2 = (1− 2,3)2 = 1,69;
[ х 2– М (Х)]2 = (2− 2,3)2 = 0,09;
[ х 3– М (Х)]2 = (5− 2,3)2 = 7,29.
Построим закон распределения этой новой случайной величины:
[ Х – М (Х)]2 1,69 0,09 7,29
Р 0,3 0,5 0,2.
Тогда
D (X) = М [ Х – М (Х)]2 = 1,69∙0,3 + 0,09∙0,5 + 7,29∙0,2 = 2,01.
■
Теорема 2. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания:
D (X) = М (Х 2) – [ М (Х)]2. (2)
○ Используя определение дисперсии и свойства математического ожидания, получим:
D (X) = М [ Х – М (Х)]2 = М [ Х 2– 2∙ Х ∙ М (Х) + М 2(Х)] = М (Х 2) – 2∙ М (Х)∙ М (Х) + М 2(Х) =
= М (Х 2) – 2∙ М 2(Х) + М 2(Х) = М (Х 2) – [ М (Х)]2. ●
На практике для вычисления D (X) чаще используют формулу (2).
Пример. Найти D (X), если Х задана законом распределения
Х 2 3 5
Р 0,1 0,6 0,3.
□
Найдем М (Х):
М (Х) = 2∙0,1 + 3∙0,6 + 5∙0,3 = 3,5.
Закон распределения случайной величины Х 2:
Х 2 4 9 25
Р 0,3 0,5 0,2.
Тогда
М (Х 2) = 4∙0,1 + 9∙0,6 + 25∙0,3 = 13,3.
Искомая дисперсия:
D (X) = М (Х 2) – [ М (Х)]2 = 13,3 − (3,5)2 = 1,05.
■
Свойства:
10. Дисперсия постоянной величины С равна нулю:
D (С) = 0.
20. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D (СX) = С 2 D (X).
30. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D (X + Y) = D (X) + D (Y).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Следствие 2. Дисперсия суммы постоянной и случайной величины равна дисперсии случайной величины:
D (С + X) = D (X).
40. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D (X − Y) = D (X) + D (Y).
○ D (X − Y) = D (X) + D (− Y) = D (X) + (−1)2 D (Y) = D (X) + D (Y). ●
Теорема 3. Дисперсия числа появления события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:
D (X) = прq.
Пример. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины Х – числа появления события в этих испытаниях.
□
По условию, п = 10, р = 0,6, q =1– р = = 0,4.
Искомая дисперсия
D (X) = прq = 10∙0,6∙0,4 = 2,4.
■
Среднее квадратическое отклонение.
Для оценки рассеяния возможных значений случайной величины вокруг её среднего значения кроме дисперсии применяют и другую числовую характеристику.
Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии
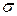 (Х) =
(Х) = 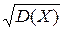 .
.
D (X) – имеет размерность, равную квадрату размерности случайной величины;
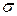 (Х) − имеет размерность, равную размерности случайной величины.
(Х) − имеет размерность, равную размерности случайной величины.
Использование D (X) или 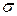 (Х) зависит от условия задачи.
(Х) зависит от условия задачи.
Пример. Случайная величина Х задана законом распределения
Х 2 3 10
Р 0,1 0,4 0,5.
Найти среднее квадратическое отклонение 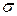 (Х).
(Х).
□
Имеем
М (Х) = 2∙0,1 + 3∙0,4 + 10∙0,5 = 6,4;
М (Х 2) = 22∙0,1 + 32∙0,4 + 102∙0,5 = 54;
D (X) = М (Х 2) – [ М (Х)]2 = 54 − (6,4)2 = 13,04;
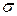 (Х) =
(Х) = 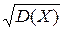 =
= 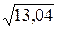 ≈ 3,61.
≈ 3,61.
■
Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равна квадратному корню из суммы квадратов средних квадратических отклонений этих величин:
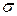 (Х 1 + Х 2 +…+ Хп) =
(Х 1 + Х 2 +…+ Хп) =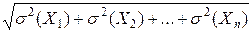 .
.
Среднее арифметическое случайных величин.
Рассмотрим п взаимно независимых случайных величин Х 1, Х 2, …, Хп, которые имеют одинаковые распределения и пусть
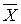 =
= 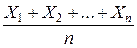 − их среднее арифметическое.
− их среднее арифметическое.
1. Математическое ожидание среднего арифметического п одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
М (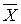 ) = а.
) = а.
2. Дисперсия среднего арифметического п одинаково распределенных взаимно независимых случайных величин в п раз меньше дисперсии D каждой из величин:
D (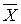 ) =
) = 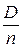 .
.
3. Среднее квадратическое отклонение среднего арифметического п одинаково распределенных взаимно независимых случайных величин в 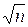 раз меньше среднего квадратического отклонения
раз меньше среднего квадратического отклонения 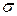 каждой из величин:
каждой из величин:
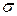 (
(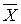 ) =
) = 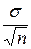 .
.
Начальные и центральные теоретические моменты.
Чтобы лучше учесть влияние на математическое ожидание того возможного значения, которое велико, но имеет малую вероятность, используют начальные и центральные моменты.
Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Хk:
νk = М (Хk).
В частности
ν 1 = М (Х), ν 2 = М (Х 2).
Пользуясь этими моментами, формулу для вычисления дисперсии
D (X) = М (Х 2) – [ М (Х)]2
можно записать в виде
D (X) = ν 2 − ν 12. (1)
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины
[ Х – М (Х)] k:
μk = M [ Х – М (Х)] k.
В частности
μ 1 = M [ Х – М (Х)] = 0, (2)
μ 2 = M [ Х – М (Х)]2 = D (X). (3)
Можно вывести соотношения, связывающие начальные и центральные моменты:
μ 2 = ν 2 − ν 12;
μ 3 = ν 3 − 3 ν 2 ν 1 + 2 ν 13;
μ 4 = ν 4 − 4 ν 3 ν 1 + 6 ν 2 ν 12 − 3 ν 14.
Моменты более высоких порядков применяются редко.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1131; Нарушение авторских прав?; Мы поможем в написании вашей работы!