Методы выбора кривых роста для выравнивания

Трудность решения задачи выбора наилучшей кривой заключается в следующем: предположим, что имеется временной ряд, состоящий из n уровней, а также полином (n-1) –го порядка, который точно описывает данный временной ряд. Кроме того, можно подобрать бесконечное число полиномов с более высоким порядком, а также функций других видов, которые с достаточной степенью точности будут аппроксимировать исследуемый временной ряд. Отдать предпочтение какой-либо одной из подобранных функций в данном случае нет оснований. Следовательно, задача заключается не в том, чтобы найти функцию, точно следующую временному ряду, а в том, чтобы подобранная функция обеспечила приемлемое согласование с имеющимися данными и при этом давала правдоподобное описание рассматриваемого явления. Последнее требование может быть выполнено, если в качестве аппроксимирующей кривой будет взята экспоненциальная, параболическая (невысокого порядка), S-образная или другие достаточно простые функции, позволяющие интерпретировать развитие изучаемого процесса.

Исходя из высказанных предположений, рассмотрим самые распространенные методы выбора кривых роста. Наиболее простой метод – визуальный. Согласно этому методу строят график временного ряда и подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на исходном графике тенденция недостаточно четко просматривается, выравнивают уровни ряда, затем строят новый график и подбирают функцию соответствующую графику выравненного ряда. Однако возможность ошибки или принятия субъективного решения при использовании визуального метода велика. Разные исследователи на основе одного итого же графика могут прийти к разным выводам при выборе формы кривой. Применение визуального подхода значительно упрощается с использованием программных средств графического изображения.

Вторым методом применяемым для выбора вида полиномиальной кривой роста является метод конечных разностей(метод Тинтнера). Этот метод может быть использован для предварительного выбора полиномиальной кривой при выполнении предположений:

1. уровни временного ряда состоят только из двух компонент: систематической составляющей (тренда) и случайной компоненты ,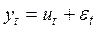

где 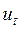- систематическая составляющая (тренд),

- случайная компонента;

2. тренд является достаточно гладким и поэтому может быть исключен либо уменьшен путем образования последовательных разностей;

3. случайная компонента подчиняется нормальному закону распределения с математическим ожиданием равным нулю и постоянной дисперсией.

Выбор кривой роста с помощью метода конечных разностей состоит в следующем:

1. Вычисляются разности k -го порядка с использованием рекурсивных отношений

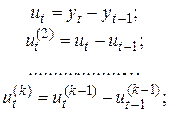
2.Вычисляются дисперсии для исходного ряда и для каждого разностного ряда по следующим формулам:

для исходного ряда по обычной формуле

,

для k -го разностного ряда по формуле

,

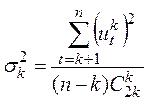где 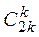— биномиальный коэффициент, значения которого приведены в таблице 3.1.

Таблица 3.1.

k

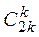
3. Вычисленное очередное значение 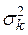сравнивается с предыдущим (k-1) значением. Процесс заканчивается при выполнении условия:

,

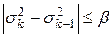где β – заранее заданная малая величина. Таким образом, расчет ведется до тех пор, пока разности не будут примерно равны друг другу. В качестве аппроксимирующего полинома принимается полином, имеющий (k-1) порядок.

Более универсальным является метод характеристик прироста, который основывается на сравнении характеристик изменения приростов исследуемого временного ряда с соответствующими характеристиками кривых роста. При рассмотрении свойств кривых роста были найдены различные преобразования приростов 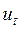, причем для каждой кривой было найдено такое преобразование 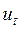, которое характеризуется линейным уравнением относительно времени. Для эмпирических рядов можно определить аналогичные характеристики, взяв вместо прироста 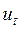значение среднего прироста . Если какая-либо из найденных по наблюдениям характеристик показывает близкое к линейному развитие во времени, то тенденция развития процесса может быть описана с помощью соответствующей кривой.

Процесс выбора кривых с использованием этого метода включает следующие этапы:

1. сглаживание ряда с помощью метода скользящей средней;

2. определение средних приростов;

3. вычисление производных характеристик прироста;

4. выбор наилучшей кривой.

Сглаживание ряда с помощью скользящей средней дает возможность наметить тенденцию изменения ряда – тренд и подготовить временной ряд к вычислению на следующем этапе средних приростов. Выравнивание многочлена лучше проводить с использованием многочлена первой степени по трем или пяти точкам по следующим формулам:

при m=3 ;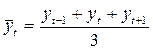

;

, .

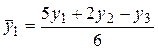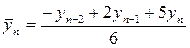при m=5 ;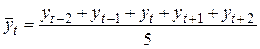

;

;

;

, .

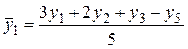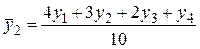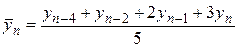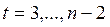Применение данных формул позволяют получить сглаженные значения для всех уровней временного ряда. Первые и последние уровни сглаживают таким образом, чтобы их не потерять.

Затем вычисляются первые средние приросты:

;

вторые средние приросты

а также ряд производных величин, связанных с вычисленными средними приростами и сглаженными уровнями ряда: 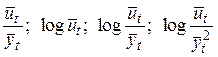. Полученные характеристики рассмотренных кривых роста сведены в таблице 3.2.

Таблица 3.2.

Показатель	Характер изменения показателя во времени	Вид кривой роста
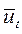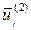
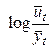
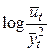
Первый средний прирост То же   Второй средний прирост	Примерно одинаковы   Изменяются линейно   Изменяются линейно   Примерно одинаковы   Изменяются линейно   Изменяются линейно   Изменяются линейно	Полином первого порядка (прямая)   Полином второго порядка (парабола) Полином третьего порядка (кубическая парабола) Простая экспонента   Модифицированная экспонента Кривая Гомперца   Логистическая кривая

Приведенные в таблице характеристики изменения показателей временных рядов исследуются на линейность и постоянство уровня. Кривые роста, характеристики которых отвечают этим условиям, выбираются в качестве аппроксимирующих для исследуемого эмпирического ряда.

Отметим, что для выбора кривых роста также можно использовать и такие критерии, как:

1. среднюю квадратическую ошибку или другими словами среднеквадратическое отклонение от тренда (выбирается кривая с наименьшим значением средней квадратической ошибки);

2. коэффициент детерминации (выбирается кривая с наибольшим значением коэффициента детерминации).

Окончательный выбор вида кривой – дело содержательного анализа, который должен охватывать не только исследование тенденций, наблюдавшихся в прошлом, но и решение вопроса о том, следует или нет ожидать сохранение этих тенденций. Таким образом, задача выбора формы кривой не решается однозначно, а сводится к получению ряда альтернатив. На практике при предварительном выборе отбирают обычно две-три кривые роста для дальнейшего исследования и построения трендовой модели данного временного ряда.

Необходимость содержательного анализа можно проиллюстрировать следующими примерами. Например, используя только математические критерии, выбирается прямая. При экстраполяции найденной закономерности в будущее по прямой, полученное прогнозное значение может быть отрицательным. Из экономической сути показателя вытекает невозможность отрицательных значений, например, при прогнозировании объема выпускаемой продукции (рис.3.9). В этом случае следует отказаться от прямой, выбрав менее подходящую по математическому критерию функцию, но более соответствующую содержательному смыслу прогнозируемого показателя.

Рис.3.9. Экстраполяция по прямой

При выборе кривых с асимптотами (модифицированной экспоненты, логистической кривой) при проведении содержательного анализа необходимо дать ответ на вопрос: возможно ли наступление «насыщения» при определенной совокупности условий. Например, процесс производства может быть ограничен производственными мощностями, материальными или финансовыми ресурсами.

Особенно осторожно следует подходить к выбору полиномов высоких степеней (третьей, четвертой степени) в качестве прогнозной модели, так как полиномы высоких степеней имеет точки разворота (рис. 3.10.). При наличии точек разворота выделенная тенденция в прогнозируемом периоде не сохраняется, а именно на этом предположении базируется применение кривых роста для прогнозирования.

Рис. 3.10. Экстраполяция по полиному 4-ой степени

Длительность интервала времени, на который cоставляется прогноз следует выбирать таким образом, чтобы после получения прогнозных оценок хватило времени на принятие управленческого решения и его эффективную реализацию. Практически бесполезно разрабатывать прогнозы на слишком короткие отрезки времени, в течение которых принятие сколько-нибудь эффективных управленческих мер оказывается невозможным.

Дата добавления: 2014-10-22