Понятие определенного интеграла

Интегрирование но частям.

Если u = u(x) vi v = v(x) - дифференцируемые функции, то фор мула интегрирования по частям имеет вид:

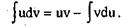Способ интегрирования по частям применяется в том случае, когда интеграл в правой части формулы более прост для вычисления, чем исходный

Пример: Вычислить

Решение: обозначим lnx через u, тогда xdx = dv. Находим:

du = d(lnx) = (lnx)^/, dx = dv/x,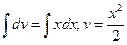

Используя формулу интегрирования по частям, получаем:

=

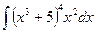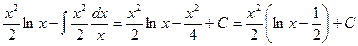
Понятие определенного интеграла широко используется в математике и прикладных науках. С его помощью вычисляют площади, ограниченные кривыми, объемы тел произвольной формы и т.д. Рассмотрим задачу по определению площади криволинейной трапе­ции, приводящую к понятию определенного интеграла.

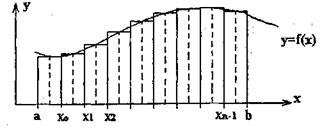
Фигура, ограниченная данной кривой у = f(x), отрезком [а,Ь] оси Ох и прямыми х = а и х = Ь, называется криволинейной трапецией

Предположим, что f(x) > 0 на отрезке [а,Ь], т.е. криволинейная трапеция расположена над осью Ох. Для вычисления площади S данной криволинейной трапеции разобьем отрезок [а,Ь] произвольным образом на п частей и обозначим точки деления:а = х₀ <x₁<x₂<…<x_n-1<x_n = b Проведя из этих точек перпендикуляры до пересечения точек с кривой, получим значение функции в этих точках:

-

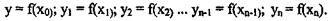
В результате площадь криволинейной трапеции окажется разбитой на сумму площадей элементарных криволинейных трапеций.

На отрезках Δх_о, Δх₁..., Δx_n-1. возьмем произвольные точки С_о, С₁, С₂,...,C_n-1 и проведем перпендикуляры из этих точек до пересечения с кривой у = f(x). Получим f(c_o), f(c₁), f(с₂),..., f(с_n-1)

Далее постоим ступенчатую фигуру, состоящую из прямоугольников, имеющим основанием отрезки Δх_о, Δх₁..., Δx_n-1, высотой –ординаты f(c_o), f(c₁), f(с₂),..., f(с_n-1) Эта фигура ограничена ломаной линией. Площадь S_n полученной ступенчатой фигуры зависит от числа п и длины отрезков Δx_i(i = О, 1, 2,..., п-1). При неограниченном увеличении числа п и уменьшении отрезка Δх_i ломанная, ограничивающая ступенчатую фигуру, будет приближаться к площади трапеции S. Отсюда ясно, что площадью криволинейной трапеции, ограниченной линией у = f(х), следует называть предел, к которому стремиться переменная площадь S_n ступенчатой фигуры, ограниченной ломаной линией, при стремлении к нулю длины отрезка Δx_i(i = О, 1, 2,..., п-1). Площадь S_n равна сумме площадей прямоугольников, построенных на отрезках:

S_n= f(c₀)Δx₀ + f(c₁)Δx₁ + …+f(c_n-1)Δx_n-1

Если теперь неограниченно увеличивая п частей разбиения так, чтобы длина отрезков Δx_i(i = О, 1, 2,..., п-1) стремилась к нулю, то площадь криволинейной трапеции будет равна пределу суммы, каждое слагаемое которой равно произведению значения функции в точке отрезка f(c_i) на величину этого отрезка Δх_i;

Если существует конечный предел этой интегральной суммы, то этот предел называется определенным интегралом от функции f(x) на отрезке [а, Ь] и обозначают:

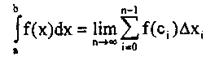
(читается «определенный интеграл от а до b от икс дэ икс»).

При этом f(x) называется подынтегральной функцией, х переменной интегрирования, числа а и b - соответственно нижним и
верхним пределом интегрирования.

Определенный интеграл есть число, его значение зависит от вида функции f(x) и значений верхнего и нижнего пределов. На основании выше изложенных формул можно записать: площадь криволинейной трапеции численно равна интегралу от функции, ограничивающей трапецию, взятому по основанию [а, Ь]:

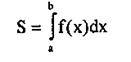
Дата добавления: 2014-10-22