Работа № 3. Арифметические циклы с простой переменной

Арифметическим называется цикл, в котором число повторений заранее известно или его можно предварительно вычислить. Название цикла связано с тем, что его параметр обычно изменяется по закону арифметической прогрессии. Если при этом параметр цикла X является простой переменной, например аргументом некоторой вычисляемой в цикле функции Y=F(X), то цикл называется арифметическим циклом с простой переменной.

Задание. Разработать блок-схемы и составить программы вычисления нижеследующих функций.

1.

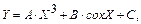
где Х изменяется от X_H =5 до Х_K =100 с шагом H=1.

Пояснение. Количество повторений в подобных циклах можно определить по формуле

N = (Х_K – Х_H)/Н + 1

с округлением (в случае дробного результата) до ближайшего целого в меньшую сторону. В нашем примере N = 96.

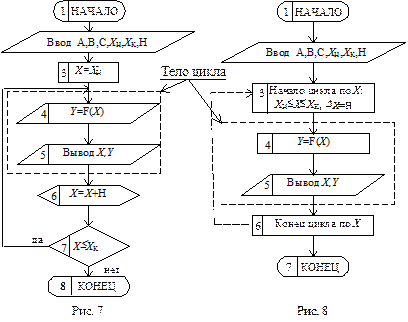
Один из возможных вариантов блок-схемы арифметического цикла для решения данной задачи представлен на рис. 7.

Блок №3, в котором переменная Х принимает свое начальное значение, называют блоком подготовки цикла. Блоки №4,5 вычисления функции Y и вывода результатов составляют рабочую часть, или тело цикла. Блок №6 является блоком изменения параметра цикла, а блок №7 – блоком проверки окончания цикла.

На многих алгоритмических языках для организации циклических программ применяются специальные операторы цикла, позволяющие упростить написание таких программ. Оператор цикла обычно объединяет в себе функции трех блоков: задания начального значения параметра цикла, его изменения и проверки окончания (блоки №3,6,7). В связи с этим может быть упрощено и начертание блок-схем, как это сделано, например, на рис. 8 для нашего примера. Но для каждого алгоритмического языка такое упрощение может быть сделано по-разному, в зависимости от особенностей оператора цикла. Далее будут использоваться два вида блок-схем циклических программ:

а) универсальная блок-схема рис. 7, приемлемая для любого языка программирования. Отметим, что здесь возможен вариант и с расположением условия выхода из цикла (блок №7) перед телом цикла. В первом случае говорят, что это цикл с постусловием, а во втором – с предусловием;

б) упрощенная блок-схема рис. 8, которая будет использоваться в более сложных циклических программах с той целью, чтобы не загромождать общую схему решения задачи излишним количеством блоков.

В последнем случае указывается только начало и конец цикла, но не указывается способ его организации. По желанию программиста эта блок-схема всегда может быть развернута до нужной в соответствии с особенностями используемого языка программирования.

Переход от одного вида блок-схемы к другому можно легко осуществить, уяснив функции соответствующих блоков из сопоставления рис. 7 и рис. 8.

Стрелка от блока №6 к блоку №3 в упрощенной блок-схеме показана пунктирной линией, так как функции возврата на повторение при использовании оператора цикла реализуются в языках программирования автома­тически без явной записи оператора перехода.

2.

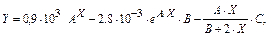
где Х изменяется от Х _Н = 0 до X _K = 10 с шагом Н = 0,5.

Из отрицательных значений функции Y сформировать массив.

Пояснение. Блок-схема решения задачи приведена на риc. 9, где идентификатором YО обозначен массив формируемых результатов, а идентификатором j – текущий индекс элементов этого массива.

В соответствии с правилами реализации типовых операций (см. приложение) до начала цикла, пока не получено ни одного результата Y, значение индекса j равно нулю (блок №3). В процессе расчетов в теле цикла, по мере нахождения очередного отрицательного значения Y (блок №7), происходит запоминание его в массив Y0 (блок № 8), которое заключается в увеличении значения индекса j и присваивании элементу массива Y0_j очередного значения Y. После окончания цикла величина j будет представлять количество элементов массива Y0, которым были присвоены отрицательные значения функции Y.

3.

где X изменяетсяот Х _H до Х _K с шагом Н.

Вычислить количество K нулевых, сумму S положительных и произведение P отрицательных значений функции Y. Вывод S и P произвести, если они вычислялись в цикле хотя бы один раз.

Пояснение. Блок-схема решения задачи приведена на рис. 10. В соответствии с правилами реализации типовых операций (см. приложение) до начала цикла задаются начальные значения К,S,Р, а непосредственно вычисление количества, суммы и произведения осуществляется в теле цикла в зависимости от значения Y. В качестве признаков необходимости вывода S и P использованы переменные KS и KP, изменяющие свои значения с нуля на единицу.

4.

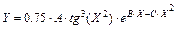
где Х изменяется от Х _H до Х _K с шагом Н, найти и вывести максимальное значение функции MAX и ее аргумент ХМ.

Пояснение. Блок-схема решения задачи приведена на рис. 11. В соответствии с правилами реализации типовых операций (см. приложение) поиск максимального значения функции осуществляется в цикле путем поочередного сравнения каждого нового значения Y с наибольшим из всех предыдущих: если Y больше МАХ (блок №6), то значение МАХ принимается равным Y и запоминается значение аргумента ХМ = Х (блок №7). В качестве первого МАХ до начала цикла принимается очень малое число (блок №3), так чтобы при первом же прохождении цикла условие блока № 6 было выполнено и МАХ получил значение первого результата Y.

5.

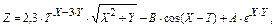
где Х изменяется от 0 до 100 с шагом H, причем

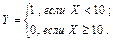
Найти минимальный результат и его порядковый номер.

6.

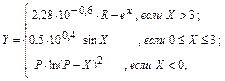
где Х изменяется от -4 до 5 с шагом 0,2. Сформировать массив всех результатов. Найти произведения положительных и отрицательных значений функции Y.

7.

где 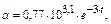t изменяется от 0 до 0,1 с шагом 0,002.

Значения функции U, большие величины С, запомнить, меньшие С просуммировать и перемножить. Найти количество значений функции U, равных C.

8.

где Х изменяется от Х _нач до X _кон с шагом H = (Х _нач - X _кон)/50.

Все результаты запоминать в массив, каждый третий результат вывести на экран. Найти суммы положительных и отрицательных результатов, а на экран вывести только сумму с наибольшим числом слагаемых.

9.

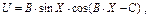
где

Все результаты запоминать в массив. Найти максимальное значение функции U и его порядковый номер, минимальное значение U и соответствующее ему значение аргумента.

Контрольное задание № 3. Составить циклическую программу вычисления функций F_m=F(X), где m=1¸10, если аргумент Х изменяется от Х _Н до Х _К с шагом Н. Вариант задания берется из табл. 3а в соответствии с номером, указанным преподавателем. Вычисляемая функция F_m вместе с вспомогательными функциямиприведена в табл. 3б. Обозначения в графе “Задание на выполнение” табл. 3а следует расшифровать в соответствии с нижеследующими списками “Обозначения искомых переменных” и “Обозначения формируемых массивов”.

Таблица 3а

№	Fm	XH	XK	H	U1	U2	W1	W2	Задание на выполнение
	F1	-2,5	7,6	0,7	9,15				S0,S1,P3,K3,R2
	F2	-3,1	3,1	0,4	1,35	-0,5		1,0	K0,S1,P1,S2,R5
	F3	0,8	8,95	0,6	-10	63,5	-25		P0,S2,P1,K1,R2
	F4	-0,2	2,85	0,3	-1,2	0,4			K0,S3,P2,P3,R0
	F5	0,85	11,3	0,8		-0,2		0,3	S0,S3,P4,K4,R5
	F6	-0,7	2,35	0,2	0,12	-0,2			P0,S3,K2,K3,R4
	F7	-1,2	2,23	0,2	0,02	0,01			S0,P3,K2,K3,R3
	F8	0,1	9,15	0,8	2,05	-0,7		1,2	P0,S2,S3,K3,R5
	F9	-0,5	5,6	0,6	2,75	-1,5			S0,P2,P3,K3,R6
	F10			0,2	0,01	0,02	-0.2		K0,S4,S1,P1,R1
	F1	-1,3	5,6	0,5		-31			P0,S4,P4,K2,R2
	F2		8,0	0,5	-2,5	0,75		0,5	P0,S1,K1,K4,R6
	F3	-0,9	2,85	0,3	3,6	-1,2			S0,S1,P2,K2,R3
	F4	-4,6	-0,8	0,4	1,05		-0,3		К0,S1,P4,К1,R1
	F5	0,1	6,28	0,5	-0,1	0,02			S0,P1,K2,K3,R4
	F6	2,5	10,3	0,8	0,9			0,5	P0,S3,K3,K1,R6
	F7	-35,2	33,5	5,1	0,8	0,5	-0,3		К0,S2,Р2,К1,R1
	F8	-9,1		0,7		1,5			S0,S2,K2,K4,R3
	F9	1,5 I	12,7	1,1		-1,5			S0,P0,P2,K4,R5
	F10			0,3		0,3			S0,P4,S2,K2,R6
	F1	-0,4	0,45	0,1	9,62	-8,3			P0,S3,P3,K2,R4
	F2	-10		0,7	3,25		-2,0		K0,S1,P3,K1,R,
	F3	-5		0,8	1,75	-0,8	4,2		S0,S4,P3,K3,R1
	F4	0,05	11,0	0,9		3,14			P0,S4,P4,K2,R4
	F5	0,05	12,3	1,1		-0,3			S0,K2.P4,K4,R3
	F6	2,15	15,0	1,1	-0,4	0,32		0,5	K0,S3,P3,K4,R6
	F7	-3,3	6,66	0,6	-0,01	0,15		0,2	S0,Р2,К2,К3,R5
	F8	-1	0,37	0,1	-1,5	0,5	-0,2		P0,S3,S4,K4,R1
	F9	-5		0,4		-1,5	-2,3		K0,P3,P2,S2,R2
	F10	0,75	9,54	0,7		0,3	-1		P0,P2,K2.K4,R1

Таблица 3б

Вычисляемая функция Fm	Вспомогательная функция

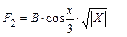
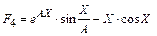
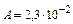
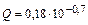
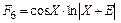
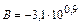
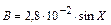
Обозначения искомых переменных:

К_n , S_n , Р_n, А_t , G_t – соответственно количество, сумма, произведение, среднее арифметическое, среднее геометрическое вычисляемых значений F _m, где индексы n и t указывают, для каких конкретных значений F _m производятся расчеты перечисленных переменных:

n = 0 – для всех результатов F_m;

1 – для результатов F_m, меньших U₁ ;

2 – для результатов F_m, меньших U₂;

3 – для результатов F_m, больших U₁;

4 – для результатов F_m, не меньших U₂ .

t = 0 – для всех результатов F_m;

1 – для результатов F_m, меньших V₁ ;

2 – для результатов F_m, меньших V₂;

3 – для результатов F_m, больших V₁;

4 – для результатов F_m, не меньших V₂ .

MIN – минимальный результат,

МАХ – максимальный результат,

МIN1 – минимальный по абсолютной величине результат,

MAX1 – максимальный по абсолютной величине результат.

Обозначения формируемых массивов:

R₀ – массив всех результатов F_m;

R₁ – массив результатов F_m, меньших W₁;

R₂ – массив результатов F_m, не меньших W₁;

R_З – массив отрицательных результатов F_m;

R₄ – массив положительных результатов F_m;

R₅ – массив модулей результатов F_m, которые по абсолютной величине

больше W₂;

R₆ – массив модулей результатов F, которые по абсолютной величине меньше W₂.

Рекомендации. Для контроля правильности получаемых результатов необходимо предусмотреть в цикле вывод таблицы расчетов функции F_m для всех аргументов в виде «аргумент X – функция F_m», по результатам которой следует производить анализ всех вычисленных значений из списка «Задание на выполнение»

Дата добавления: 2014-10-23