A. Подготовка уравнения, пригодного для итерации

Заданное уравнение F (X)=0 при решении методом итерации должно быть преобразовано к виду Х =φ(X), для которого обязательно выполнение условия сходимости, записанного в виде½φ'(Х)½<1, то есть модуль производной от φ(X) на заданном интервале изоляции корня [ A,B ] должен быть меньше 1. Возможны два способа получения уравнения вида Х = φ(X).

Первый способ заключается в простом выделении какого-либо X из исходного уравнения F (X) = 0, как это было сделано в примере первого задания данной работы. После этого необходимо взять производную от правой части полученного уравнения φ'(X) и подставить в нее поочередно X=A и X=B. Если при этом |φ'(A)|<1 и |φ'(B)|<1, то уравнение Х =φ(X) считается пригодным для решения методом итерации. Однако такой подход равносилен лотерее: можно выделять различные X из исходного уравнения, но так и не получить решение, удовлетворяющее условию сходимости.

Второй способ дает гарантированное решение, поскольку в основе его изначально заложено выполнение условия сходимости. Заключается он в следующем.

Исходное уравнение F (X) = 0 заменяется на эквивалентное:

Х = Х – F (X) / K,

где К – коэффициент, обеспечивающий сходимость итерационного процесса, выбирается на основании двух требований:

1) знак К должен совпадать со знаком производной F '(X) на данном интервале изоляции корня [ A,B ];

2) значение К по модулю должно быть больше половины максимального значения модуля производной на интервале изоляции корня [ A,B ]:

Например, при решении уравнения F (X)= X ³– X –1 = 0 на интервале [1,2] находим:

1) F ' (X) = 3× X² -1 > 0, то есть К должен быть положительным;

2) ½ F ' (X)½_max = 11, то есть К > 11/2. Возьмём К = 6.

Тогда окончательное уравнение, пригодное для решения методом итерации, будет иметь вид

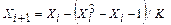, где K =6.

Дата добавления: 2014-10-23