Передаточные функции элементов

Пример составления математического описания

Система регулирования скорости двигателя, постоянного тока, функциональная схема которой показана на рис. 3.35, включает в себя: объект управления, двигатель постоянного тока независимого возбуждения (Д); исполнительный орган – преобразователь (П); регулятор, реализующий пропорционально-интегральный (ПИ) закон регулирования и датчик скорости – тахогенератор (ТГ). Все четыре перечисленные элементы соединены в систему управления с отрицательной обратной связью по скорости.

Первичная форма описания

(дифференциальные и алгебраические уравнения)

Уравнения двигателя (см. п. 2.2.):

U _я – E = i _я R _я + L _я(di _я/ dt), (3.9)

E = c_eФ w, (3.10)

М _д = с_мФi _я (3.11)

J (d w/ dt) = М _д – М _c (3.12)

Уравнение преобразователя

U _п = U _я + i _я R _п + L _п(di _я/ dt) (3.13)

Уравнение тахогенератора

U _тг = k _тгw. (3.14)

Уравнение регулятора

U _р = k _р(U _з - U _тг) + k _iò(U _з - U _тг) dt, (3.15)

где U _п, R _п и L _п – напряжение, сопротивление и индуктивность преобразователя;
U _з – задающее скорость напряжение; k _тг – коэффициент передачи тахогенератора; k _р и k _i – коэффициенты пропорциональной и интегральной составляющих регулятора.

Передаточная функция якорной цепи двигателя. Объединяя (3.9) и (3.13), получим U _п = Е + i _я(R _п + R _я) + (L _п + L _я) (di _я/ dt) = Е + i _я R _яц(1 + Т _яц р),

где R _яц = R _п + R _я; Т _яц = L _яц/ R _яц; L _яц = L _п + L _я; р = d/dt.

Преобразуем обе части по Лапласу

U _п(s) = Е (s) + I_я(s) R _яц(1 + Т _яц s).

Составляем передаточную функцию якорной цепи

.

Передаточная функция механической части двигателя. Преобразуем по Лапласу (3.12) и получаем

Js w = М _д(s) – М _c(s),

Откуда передаточная функция механической части

.

Передаточная функция противо ЭДС двигателя

.

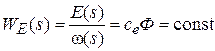Передаточная функция преобразователя

.

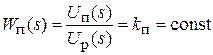Передаточная функция регулятора

.

U _п = U _я + i _я R _п + L _п(di _я/ dt), (3.16)

Уравнение тахогенератора

U _тг = k _тгw, (3.17)

Уравнение регулятора

U _р = k _р(U _з – U _тг) + k _iò(U _з – U _тг) dt, (3.18)

где U _п, R _п и L _п – напряжение, сопротивление и индуктивность преобразователя;
U _з – задающее скорость напряжение; k _тг – коэффициент передачи тахогенератора; k _р и k _i – коэффициенты пропорциональности и интегральной составляющей регулятора.

Структурная схема системы

На основании записанных выражений передаточных функций отдельных элементов составляем общую структурную схему системы (рис. 3.36).

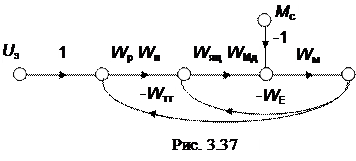По структурной схеме (рис. 3.36) составляем граф системы (рис. 3.37).
По графу с помощью правила Мейсона Определяем передаточную функцию двигателя по управляющему воздействию:

где k _и = 1/ c_eФ – коэффициент передачи двигателя по напряжению;
T _эм = JR _яц/ c_ec_мФ² – электромеханическая постоянная времени двигателя.

Таким образом, по управлению напряжением на якоре двигатель постоянного тока может быть представлен моделью звена второго порядка.

Аналогичным образом можно получить выражение передаточной функции двигателя по моменту сопротивлений М _с.

Дата добавления: 2014-10-31